Долучіться до технологічної революції, що захоплює фінансовий світ як шторм. Опановуючі Bitcoin є вашим провідником по, здавалось би, складному світові біткоіну, провадячи потрібні вам знання щоб приймати участь в інтернеті грошей. Чи ви будуєте наступне вбивче застосування, інвестуєте в стартап, або просто цікавитесь цією технологією, це перероблене та розширене друге видання провадить основні деталі, з яких ви маєте починати.
адреса біткоін виглядає як 1DSrfJdB2AnWaFNgSbv3MZC2m74996JafV. Вона складається з рядка літер та чисел. Насправді це закодована версія base58check публічного ключа 160-бітного хешу. Так само, як ви просите вислати поштову адресу на вашу адресу, ви можете запитати надіслати вам біткоіни на одну з ваших біткоін адрес.
bip, Bitcoin Improvement Proposals. Набір пропозицій
від членів спільноти, надісланих для покращення біткоіна. Наприклад,
BIP-21 є пропозиція покращити схему біткоінівськіх ідентифікаторів
ресурсів (URI).
біткоін є назвою грошових одиниць (монет), так само як
мережі та програмного забезпечення.
блок - група транзакій, що помічені часовою відміткою, та відтиск від попереднього блоку. Заголовок блоку захешовано для отримання підтвердження виконаної роботи, що підтверджує транзакції. Валідні блоки додаються до блокчейну через мережевий консенсус.
блокчейн є списком валідних блоків, кожний пов'язаний зі своїм попередником, і далі так само, до первинного блоку.
проблема візантійськіх генералів. Надійна комп'ютерна
система має бути в змозі мати справу з одним або більше відмовами однієї
або більше своїх компонент. Збійний компонент може виказувати тип
поведінки, на яку зазвичай не звертають уваги — а саме, надсилати
конфліктуючу інформацію до різних частей системи. Проблема при спілкуванні
з такими збоями абстрактно виражена через проблему візантійськіх
генералів..
коінбейс - спеціальне поле, що використовується як єдине джерело для транзакцій коінбейс. Коінбейс дозволяє підтвердити отримання нагороди за підпис блоку, та провадить 100 байтів довільних даних. На слід плутати з коінбейс транзакціями.
коінбейс транзакція - перша транзакція в блоку. Завджи
створюється майнером, та включає єдиний коінбейс. Не плутати з самим
коінбейс.
холодне сховище посилається на зберігання біткоінів
офлайн. Холодне сховище утворюється через створення та зберігання
приватних ключів Bitcoin в безпечному оточенні офлайн. Холодне сховище
важливе для будь-кого, що має накопичення біткоінів. Комп'ютери онлайн є
вразливі для хакерів, та не мають використовуватись для зберігання
важливої кількості біткоінів.
кольорові монети. Відкритий код протоколу Bitcoin
2.0 дозволяє розробникам створювати цифрові активи зверху
блокчейну, використовуючи його функціональність за межами грошового обігу.
підтвердження. Коли транзакція включається в блок, вона має одне підтвердження. Коли майнається інший блок в тому ж блокчейні, транзакція матиме два підтвердження, і так далі. Шість підтверджень вважаються достатнім підтвердженням, що транзакція не може бути відмінена.
консенсус - коли декілька вузлів, звичайно, більшість вузлів в мережі, всі мають ті самі блоки в своїх найкращих валідованих ланцюжках блокчейну. Не плутати з правилами консенсусу.
правила консенсусу - правила перевірки блоків, якім слідують повні вузли, щоб залишатись в стані консенсусу з іншими вузлами. Не плутати з консенсусом.
складність - налаштування рівня мережі, що контролює,
скільки обчислень потрібно для продукування підтвердження виконанної
роботи.
переорієнтування складності - переобчислення для всієї мережі складності, що трапляється кожні 2,016 блоків, та приймає до уваги потужність хешування попередніх 2,016 блоків.
цільова складність - складність, з якою всі обчислення в
мережі будуть знаходити блоки з апроксімацією кожні 10 хвилин.
подвійне витрачання є результатом успішного використання
деяких грошей більше ніж один раз. Bitcoin захищений від подвійного
витрачання через верифікацію транзакцій, доданих до блокчейну, щоб
переконатись, що всі входи для транзакції наразі не були витрачені до
цього.
ECDSA, Elliptic Curve Digital Signature Algorithm є
криптографічним алгоритмом, що використовує Bitcoin, щоб переконатись, що
фонди можуть бути витрачені своїми справжніми власниками.
додатковий довісок. По мірі зростання складності майнери часто проходять всі 4 мільярди значень довіска, не знайшовши блок. Оскільки скрипт коінбейс може зберігати від 2 до 100 байтів даних, майнери починають використовувати цей додатковий простір як додатковий довісок, що дозволяє їм досліджувати значно більший диапазон значень заголовка блока, та знайти значення блока.
(комісійні) збори. Надсилач транзакції часто включає комісію для
мережі за обробку запитаної транзакції. Більшість транзакцій потребують
мінімальні комісійні в 0.5 mBTC.
відгалуження, також відоме як випадкове відгалуження,
трапляється, коли два або більше блоків мають ту саму висоту блоку, даючи
розгалуження блокчейну. типово трапляється, коли два або більше майнери
знаходять блоки в той самий час. Також може трапитись як частина атаки.
первинний блок - перший блок в блокчейні,
використовується для ініціалізації крипто валюти.
жорстке розгалуження, також відоме як зміна жорсткого
розгалуження, є постійне розділення блокчейну, загалом трапляється, коли
неоновлені вузли не можуть перевірити блоки, створені оновленими вузлами,
що слідують новим правилам валідації. Не плутати з розгалуженням, м'яким
розгалуженням, програмним розгалуженням та розгалуженням Git.
апаратний гаманець є спеціальним типом гаманця біткоін,
що зберігає приватні ключі користувача на безпечному апаратному пристрої.
хеш - цифровий відтиск деякого бінарного значення.
хеш блокування є типом перешкод, що обмежує витрату входу, докі деяка вказана частина даних не буде публічно розкрита. Хеш блокування має корисну властивість, що коли одне з блокувань стає розкритим публічно, любі інші хеш блокування, захищені тим самим ключем, також можуть бути відкриті. Це робить можливим створити декілька виходів, зачинених тим самим хеш блокуванням, та які всі стає можливо витрачати одночасно.
протокол HD, Hierarchical Deterministic (HD), протокол для створення та передачі ключів (BIP32), що дозволяє створення дочірніх ключів від батьківськів в ієрархії.
гаманець HD використовує Hierarchical Deterministic (протокол HD) для створення ключів (BIP32).
зерно HD гаманця, або кореневе зерно є потенційно
short value used as a seed to generate
the master private key and master chain code for an HD wallet.
HTLC Hashed TimeLock Contract, контракт з хешованим
часовим замком, є класом платежів, що використовують хеш блокування та
часові замки, що потребують, щоб отримувач платежу або підтвердив
отримання платежу до визначенного терміну, через генерацію підтвердження
платежу, або він втрачає здатність претендувати на платіж, повертаючи його
платникові.
KYC Know your customer, знай свого клієнта - процес в
бізнесі, ідентифікуючий та верифікуючий його клієнтів. Термін також
використовується на банківське регулювання, що регулює ці дії.
LevelDB є відкритим сховищем ключ-значення на диску.
LevelDB є легковажною бібліотекою єдиного призначення зберігання, що має
прив'язки до багатьох платформ.
Lightning Networks є запропонованою реалізацією Hashed
Timelock Contracts (HTLC) з дво-спрямованими каналами платежів, що
дозволяє безпечне переправлення платежів через різноманітні канали
платежів сторона-до-сторони. Це дозволяє формування мережі, де кожна
сторона в мережі може заплатити кожному іншому, навіть якщо вони напряму
не мають відкритого каналу один до одного.
Locktime, або більш технічно nLockTime, є частиною
транзакції, що вказує на найменьший час, або найранішній блок, коли
транзакція може бути додана до ланцюга блоків.
mempool, блокчейн мемпул (пул в пам'яті) є
колекцією з усіх даних транзакцій в блоці, що були перевірені вузлами
біткоін, але все ще не підтверджені.
мерклівській корінь - кореневий вузол мерклівського
дерева, нащадок всіх хешованих пар в дереві. Заголовки блоків мають
включати валідний мерклівський корінь, що походить з усіх транзакцій в
блоці.
мерклівське дерево, дерево, створене через хешування
попарних даних (листів), що потім збираються попарно, та хешуючи
результат, доки не залишиться єдиний хеш, мерклівській корінь. В Bitcoin
листами майже завжди є транзакції з одного блоку.
майнер - вузол мережі, що шукає валідний доказ
проробленої роботи для нових блоків, через циклічне хешування.
мультисигнатура - multisig, посилаєтсья на вимогу мати
більше ніж один ключ для авторизації транзакції біткоін.
мережа, поєднання сторона-до-сторони, що просуває
транзакції та блоки до кожного вузла біткоін в мережі.
довісок є полем в блоці біткоін, розміром 32-біти (4
байти), чиє значення встановлюється так, щоб хеш блоку містив задану
кількість першух нулів. Залишок полів не можуть були змінені, бо вони
мають визначене значення.
поза-ланцюгові транзакції - переміщення значень за
межами блокчейну. Тоді як ланцюгові транзакції — на які звичайно
посилаютсья як на прості транзакції — модифікують блокчейн, та залежать
від блокчейну для визначення власної валідності, поза-ланцюгові транзакції
покладаються на інші методи для запису та перевірки транзакції.
коди операцій, opcode - коди мови Bitcoin Script, що
засувають дані або виконують функції в скрипті pubkey або signature.
протокол Open Assets є простий та потужний протокол,
побудований на блокчейні біткоіна. Він дозволяє випуск та передачу
створених користувачем активів. Протокол Open Assets є розвитком концепції
кольорових монет.
OP_RETURN - код операції, використаний в одному з
виходів в транзакції OP_RETURN. Не треба плутати з транзакцією OP_RETURN.
транзакція OP_RETURN - тип транзакції, що передається та майниться по
замовченню в Bitcoin Core 0.9.0 та пізніших, що додає довільні дані до
доказового скрипта невитратного pubkey, що повні вузли не мають зберігати
в своїй базі даних UTXO. Не плутати з кодом операції
OP_RETURN.
очікуючий (підвислий) блок - блок, чий батьківській блок
ще не був оброблений локальним вузлом, так що він наразі не може бути
валідований.
очікуючі (підвислі) транзакції - такі транзакції, що не
можуть іти в пул через одну або більше вхідних транзакцій.
вихід, вихід транзакції або TxOut є вихід в транзакції,
що містить два поля: поле значення для нуля або більше сатоші, та скрипт
pubkey, для встановлення, яким умовам треба задовільняти, щоб витратити ці
сатоші.
P2PKH - транзакції, що сплачуються на адресу біткоін, що
містить P2PKH або скрипт Pay To PubKey Hash. Вихід, що заблоковано
скриптом P2PKH, може бути розблокований(витрачений), через пред'явлення
публічного ключа та цифрового підпису, створеного відповідним приватним
ключем.
P2SH або Pay-to-Script-Hash - потужний новий тип
транзакцій, що значно спрощує використання складних скриптів транзакцій.
За допомогою P2SH складний скрипт, що перелічує умови для витрати виходу
(повторний сценарій) не представлений в блокуючому скрипті. Замість цього
там є лише хеш цього скрипта.
P2SH адреса є Base58Check кодуванням 20-байтного хешу
скрипта. P2SH адреса використовує префікс “5”, що призводить до того, що
Base58Check-кодована адреса починається з “3”. P2SH адреса приховує всю
складність, так що людина, що робить платіж, не бачить скрипта.
P2WPKH - сигнатура P2WPKH
(Pay-to-Witness-Public-Key-Hash), містить ту саму інформацію, що і витрата
P2PKH, але розташована в полі доказу, замість поля scriptSig. Також
scriptPubKey є модифікований.
P2WSH. Різниця між P2SH та P2WSH
(Pay-to-Witness-Script-Hash) полягає в розміщенні криптографічного
підтвердження, що змінене з поля scriptSig до поля свідоцтва, та
scriptPubKey також модифікований.
паперовий гаманець, в найбільш специфічному сенсі, є
документом, що містить всі дані, потрібні для генерації любого числа
приватних ключів Bitcoin, формуючи гаманець з ключами. Однак люди часто
використовують цей термін, маючи на увазі любий спосіб зберігання
біткоінів офлайн, як фізичний документ. Це друге визначення також включає
паперові ключі, та погашувальні коди.
канали платежів - канал мікроплатежів або канал платежів
є прийомом, розробленим щоб дозволити користувачам робити багато
транзакцій с біткоіном, без підтвердження всіх транзакцій в біткоін
блокчейні. В типовому каналі платежів тільки дві транзакції додаються до
блокчейна, але необмежене, або майже необмежене число платежів можуть бути
зроблені між задіяними сторонами.
майнинг в пулі - підхід до майнингу, коли багато
генеруючих клієнтів докладаються до генерації блоку, та потім поділяють
винагороду згідно вкладеній оброблюваній потужності.
Proof-of-Stake, (PoS), доказ ставок, є методом, яким
мережа крипто валюти з блокчейном досягає розподіленого консенсусу.
Proof-of-Stake запитує користувачів доказати власність певної кількості
валюти (їхню “ставку” в валюті).
підтвердження виконанної роботи, Proof-of-Work - частина
даних, що потребує виконання значних обчислень, щоб бути знайденою. В
біткоіні, майнери мають знайти числове рішення алгоритма SHA256,
що задовільняє мережевій цільовій складності.
винагорода - сума, що вкладається в кожний новий блок,
як винагорода від мережі майнеру, хто знайшов рішення підтвердження
виконанної роботи. На сьогодні це 12.5 BTC за блок.
RIPEMD-160 є 160-бітною криптографічною хеш функцією.
RIPEMD-160 є посиленою версією RIPEMD з 160-бітовим результатом хеша, та
очікується, що буде безпечною протягом найближчих десяти років, або
більше.
сатоші є найменьшою одиницею обміну біткоінами, що може
бути записана в блокчейні. Вона еквівалентна 0.00000001
біткоінам та названа на честь створювача Bitcoinа, Satoshi Nakamoto.
Satoshi Nakamoto - ім'я, використане персоною або
людьми, хто розробив Bitcoin та створив оригінальну референсну реалізацію,
Bitcoin Core. Як частина реалізації, вони також розробили першу базу даних
блокчейна. В процесі вони першими вирішили проблему подвійної витрати для
цифрових грошей. Їх дійсні імена залишаються невідомими.
скрипт. Bitcoin використовує скриптову систему для
транзакцій. Система скриптів проста та скидаєтсья на Forth, базується на
стеку, та обробляється зліва направо. Вона навмисно не Т'юрінг-повна, бо
не має циклів.
скрипт ScriptPubKey (також скрипт pubkey) - скрипт,
включений в вихід, що встановлює умови, яким треба задовільняти, щоб
витратити ці сатоші. Дані, потрібні щоб задовільнити умовам, мають бути
запроваджені в скрипті.
підпис ScriptSig (також скрипт сигнатури) - дані,
згенеровані тим, хто витрачає, що майже завжди використовуються як змінні,
щоб задовільнити скрипт pubkey.
секретний ключ (він же приватний ключ) - секретне число,
що відкриває біткоіни, надіслані на відповідну адресу. Секретний ключ
виглядає таким чином: 5J76sF8L5jTtzE96r66Sf8cka9y44wdpJjMwCxR3tzLh3ibVPxh
відокремлене свідоцтво є запропоноване оновлення до
протоколу Bitcoin, що є технологічною іновацією, яка відокремлює дані
підпису від транзакцій біткоін. Відокремлене свідоцтво є запропонованих
м'яким відгалуженням; ця зміна технічно робить протокол Bitcoin більш
обмежуючим.
SHA, Secure Hash Algorithm, або безпечний хеш-алгоритм,
є сімейство кріптографічних хеш функцій, опублікованих Національним
інститутом стандартів та технології (NIST).
SPV, simplified payment verification, або спрощена
верифікація є метод для верифікації часткових транзакцій, що включені в
блок, без завантаження самого блоку. Метод використовується в деяких
легковажних клієнтах Bitcoin.
м'яке розгалуження, або зміна м'якого розгалуження є
тимчасовим розгалуженням в блокчейні, що загалом трапляється, коли майнери
використовують неоновлені вузли, що не слідують новим правилам консенсусу,
про який вони не знають. Не плутати з розгалуженням, жорстким
розгалуженням, програмних розгалуженням та розгалуженням Git.
стабільний блок - такий, що успішно змайнений, але не
включений в поточний кращий ланцюжок блокчейн, вірогідно тому, що деякий
інший блок з такою самою висотою розширив блок раніше.
часове блокування є типом перешкод, що обмежує витрату біткоінів до вказаного часу в майбутньому, або до заданої висоти блоку. Часове блокування яскраво використовується в багатьох контрактах Bitcoin, включаючи платіжні канали та контракти з хешовим блокуванням.
транзакція, в простих термінах, є передача біткоінів з
однієї адреси до іншої. Більш точно, транзакція є підписана структура
даних, що виражає передачу значення. Транзакції передаються через мережу
біткоін, збираються майнерами, та включаються в блоки, стаючи постійними в
блокчейні.
пул транзакцій - невпрорядкована колекція транзакцій, що
не є в блоках основного блокчейну, але для яких ми маємо вхідні
транзакції.
повнота Т'юрінга. Мова називається повною за Т'юрингом,
якщо вона може використати любу програму, що може виконати машина
Т'юрінга, маючи досить чису та пам'яті.
невикористані вихідні транзакції, unspent transaction
output (UTXO) є вихідними транзакціями, що можуть бути витрачені в
наступних вхідних транзакціях.
гаманець є програмою, що зберігає всі біткоін адреси та
секретні ключі. Використовується для надсилання, отримання та зберігання
ваших біткоінів.
Wallet Import Format (WIF) - формат обміну даними,
розроблений щоб дозволити експорт та імпорт одного приватного ключа з
флагом, що вказує, чи використовується стискання публічного ключа, або ні.
Bitcoin є набором концепцій та технологій, що формують основу цифрової грошової екосистеми. Грошові одиниці, що називаються біткоін (біткоінами) використовуються для зберігання та передачі вартості між приймаючими участь в мережі біткоін. Користувачі біткоін комунікують один з одним, використовуючи біткоін протокол, в основному через інтернет, хоча інші транспотртні мережі також можуть бути використані. Стек протоколу біткоін, доступний як програма з відкритим кодом, може виконуватись на великому диапазоні обчислювальних приладів, включаючи лептопи та смартфони, що робить технологію легко доступною.
Користувачі можуть передавати біткоін через мережу, щоб робити все те саме, що може бути зроблене зі звичайними грошима, включаючи придбання та продаж товарів, надсилання грошей іншим людям або організаціям, або отримання кредиту. Біткоін може бути придбаний, проданий та обміняний на інші валюти на спеціалізованих обмінниках валют. Біткоін в деякому сенсі є ідеальною формою грошей для інтернета, бо він є швидкий, безпечний та необмежений кордонами.
На відміну від традиційних валют, біткоін є повністю віртуальним. Немає фізичних монет, або навіть цифрових монет, як таких. Монети маються на увазі в транзакціях, що передають вартість від надсилача до отримувача. Користувачі біткоін володіють ключами, що дозволяють їм підтвердити власність на біткоіни в мережі біткоін. За допомогою ціх ключів вони можуть підписувати транзакції, щоб відімкнути (розблокувати) вартість, та витратити її, передавши новому власнику. Ключі часто зберігаютья в цифровому гаманці на комп'ютері або смартфоні кожного користувача. Володіння ключем, що може підписати транзакцію, є єдиною передумовою для витрачання біткоінів, передаючи контроль повністю в руки кожного користувача.
Біткоін є розподіленою системою сторона-до-сторони. Як такого, немає
“центрального” сервера або точки контролю. Біткоін створений через процес,
що називається “майнингом”, що включає змагання за пошук рішень
математичної проблеми, при цьому обробляючи транзакції біткоін. Любий, хто
приймає участь в мережі біткоін, (тобто, кожний, хто використовує
пристрій, що виконує повний стек протоколу біткоін), може оперувати як
майнер, використовуючи свою ообчислювальну потужність для перевірки та
запису транзакцій. Кожні 10 хвилин, в середньому, майнер біткоін є в змозі
перевірити транзакції за останні 10 хвилин, та винагороджується повністю
новими біткоінами. В своїй основі, біткоін майнинг децентралізує випуск
грошей та функції клірингу (підтвердження та закріплення транзакцій)
замість центрального батнку, та заміняє потребу в центральному банку.
Біткоін протокол включає вбудовані алгоритми, що регулюють функцію майнингу по всій мережі. Складність завдання обробки, що мають виконати майнери, динамічно підлаштовується, так, щоб дехто отримував успіх кожні 10 хвилин, безвідносно до того, як багато майнерів (та як багато обчислень) змагаються наразі в кожний момент.
Протокол також переділяє навпіл рівень, з яким створюється біткоін, кожні 4 роки, та обмежує загальне число біткоінів, що будуть створені до фіксованого загалу меньше 21 мільйонів монет. Результат цієї кількості біткоінів в обігу близько слідує добре передбачуваній кривій, що досягає 21 мільйонів в 2140 році. Через зниження швидкості карбування біткоінів, в довгій перспективі, валюта біткоіну є дефляційною. Більше того, біткоін не може бути інфльований через “друк” нових грошей далі же межами очікуванної кількості випущенних монет.
За лаштунками сцени біткоін також є назвою протоколу, мережі сторона-до-сторони, та інноваційного розподіленого обчислення. Валюта біткоіна насправді є тільки першим застосуванням цього винаходу. Біткоін представляє кульмінацію десятирічь дослідів в криптотграфії та розподілених системах, та включає чотири ключові інновації, складені разом в унікальний та потужній комбінації. Біткоін складається з:
• Децентралізованої мережі сторона-до-сторони (протокол біткоін)
• Публічний реєстр транзакцій (блокчейн)
• Набір правил для незалежної валідації транзакцій та випуску грошей (правила консенсусу)
• Механізм для досягнення децентралізованого консенсусу на валідному блокчейні (алгоритм доказу виконаної роботи)
Як розробник, я дивлюсь на біткоін, як щось подібне на інтернету грошей, мережа, що просуває цінність та захищає власність на цифрові активи через розподілені обчислення. В біткоіні є значно більше, ніж впадає в око з першого погляду. В цій главі ми почнемо досліджувати деякі з головних концепцій та термінів, отримаємо необхідне програмне забезпечення, та використаємо біткоін для простих транзакцій. В наступних главах ми почнемо розгортати нашарування технологій, що роблять біткоін можливим, та дослідимо внутрішню роботу мережі та протоколу біткоін.
Створення життєспроможньіх цифрових грошей тісно пов'язане з розробками в криптографії. Не стало сюрпризом, коли дехто розглядає фундаментальні виклики, використовуючи біти для представлення вартості, що можуть бути обміняні на товари та послуги. Три основні запитання постають для кожного, хто приймає цифрові гроші, і вони наступні:
1. Можу я довіряти тому, що ці гроші справжні та не є підробними?
2. Можу я довіряти тому, що цифрові гроші можуть бути витрачені один раз
(відоме як проблема “подвійної витрати”)?
3. Чи можу я бути впевнений, що ніхто інший не зможе переконати, що гроші
належать йому, та не мені?
Друкарі паперових грошей постійно ведуть боротьбу з проблемою підробок, через застосування все більш складні папір та технології друку. Фізичні гроші вирішують проблему подвійної витрати, бо той самий папір не може знаходитись в двох місцях одночасно. Зрозуміло, що звичайні гроші також часто зберігаютсья та передаються в вигляді транзакцій. В ціх випадках, підробка та проблема подвійної витрати обробляються через очищення всіх електронних транзакцій в центральних установах, що мають глобальний погляд на всі гроші в обігу. Для цифрових грошей, що не можуть отримати переваги від застосування езотеричних чорнил або голограмних стрічок, криптографія провадить основу для довіри легитимності претензій користувача щодо прав власності. Більш детально, криптографічні цифрові підписи дозщволяють користувачеві підписувати цифрові активи або транзакції, що провадить власність щодо цього активу. З відповідною архитектурою, цифрові підписи також можуть бути використані для вирішення проблеми подвійної витрати.
Коли криптографія почала ставати більш широко доступною, та стала
зрозумілою в кінці 1980-х, багато дослідників почали спроби
використовувати криптографію для побудови цифрових валют. Ці ранішні
проекти цифрових грошей випускали цифрові гроші, часто підтримані
національними валютами, або дорогоцінними металами, такими як золото.
Хоча ці ранішні цифрові валюти прауювали, вони були централізовані, та, як результат, було простим для атаки з боку урядів та хакерів. Ранішні цифрові гроші використовували центральні клірингові установи для закріплення всіх транзакцій з регулярними інтервалами, так само, як традиційна банківська система. На жаль, в більшості випадків ці незрілі цифрові валюти ставали ціллю занепокоєних урядів, та з часом судилися аж до зникнення. Деякі схибили через феєричні падіння, коли батківська компанія раптово ліквідувалась. Щоб бути стійким до нападів антагоністів, чи то суперечки з урядами, або кримінальними елементами, була потрібна розподілена валюта, щоб уникнути єдиної точки атаки. Біткоін є саме такою системою, децентралізованою від народження, та вільна від жодної центральною цстанови, або точки контролю, що може бути атакована або пошкоджена.
Bitcoin був винайдений в 2008-му році, коли була опублікована стаття
“Bitcoin: A Peer-to-Peer Electronic Cash System”, написана під псевдонімом
Satoshi Nakamoto (https://bitcoin.org/bitcoin.pdf, дивіться Додаток
A). Nakamoto зібрав декілька попередніх винаходів, таких, як b-money та
HashCash, щоб створити повністю децентралізовані електронні гроші, що не
покладаються на центральну установу для випуску грошей, або закріплення та
валідацію транзакцій. Ключовим винаходом було використання розподіленої
системи обчислень (що назівається алгоритмом доказу виконаної роботи), щоб
проводити глобальні “вибори” кожні 10 хвилин, дозволяючи децентралізованій
системі досягати консенсусу щодо стану транзакцій. Це елегантно вирішує
проблему подвійної витрати, коли одна сума може бути витрачена двічи. До
цього проблема подвійної витрати була слабкістю цифрових грошей, та
вирішувалась через очищення всіх транзакцій через централізовану
клірингову установу.
Мережа біткоін стартувала в 2009-му році, базуючись на референсній реалізації, опублікованій Nakamoto, та з тих пір перевіреною багатьма іншими програмістами. Реалізація алгоритма доказу виконаної роботи (Proof-of-Work), також відомому як майнінг, що провадить безпеку та стійкість, зростаючі в експоненціальній ступіні, та наразі перевищує загальну потужність всіх найпотужних суперкомп'ютерів. Загальна ринкова вартість Bitcoin ставала часом більше $35 мільярдів доларів США (на кінець 2017 загальна кількість біткоін складає 17 мільйонів, вартістю біля 92 млрд. долларів ), в залежності від курсу долара до біткоіна. Найбільша оброблена транзакція, що досі проходила в мережі, складала $150 мільйонів доларів, вони були передані напряму та оброблені без жодних комісійних.
Satoshi Nakamoto віддалився з публіки в 2011-му році, залишивши відповідальність за розробку кода та мережі на процвітаючу групу добровольців. Особистість людини або групи людей, що стоять за біткоіном, все ще невідома. Однак ані Satoshi Nakamoto, так само, як ніхто інший не має індивідуальний контроль над системою біткоін, що робить на базі прозорих математичних принципів, відкритого джерельного коду, та консенсусу між задіяними сторонами. Саме відкриття настільки новаторське, та вже породив нову науку в сфері розподіленого обчислення, економіки та економетрики.
Винахід Satoshi Nakamoto також є практичним та новітнім рішенням проблеми розподілених обчислень, відомої як проблема візантійськіх генералів. Скорочено, ця проблема складається в намаганні скласти домовленість щодо стану системи, через обмін інформацією через ненадійну, та потенційно скомпроментовану мережу. Рішення Satoshi Nakamoto, що використовує концепцію доказу виконаної роботи для досягнення консенсусу без центральної установи, предсатвляє прорив в розподіленоих обчисленнях, та має застосування за межами валюти. Воно може використовуватись для досягнення консенсусу в розподілених мережах, щоб довести чесність виборів, лоторей, реєстрів рахунків, цифрових нотаріусів, і багато більше.
Біткоін є інновацією в старовинній технології грошей. В своїй основі гроші просто спрощують обмін вартістю між людьми. Таким чином, щоб повністю зрозуміти біткоін та його використання, ми подивимось на нього з перспективи людей, що використовують його. Кожний з людей та їх історій, які перелічено тут, ілюструє одну або більше зі специфічних способів використання. Ми побачимо їх на протязі цієї книги:
Аліса живе в районі затоки Північної Каліфорнії. Вона чула про біткоін від своїх друзів, та почала використовувати їх. Ми прослідкуємо її історію, як вона пізнала про біткоін, як отримала декілька, та потім витратила свої біткоіни для придбання філіжанки кави в кав'ярні Боба в Пало Альто. Ця історія дасть вам вступ до програмного забезпечення, обміну, та базових транзакцій з перспективи продавця нерухомості.
Керол є власницею арт галереї в Сан Франциско. Вона продає коштовні малюнки за біткоін. Ця історія буде включати ризик консенсус-атаки “51%” для продавців коштовних речей.
Боб, власник кав'ярні в Пало Альто, будує новий веб сайт. Він виняйняв по контракту індійського веб розробника, Гопеша, що живе в Банглорі, Індія. Гопеш погодився отримати платню в біткоіні. Ця історія перевірить використання біткоіну для аутсорсінгу, контрактних послуг, та міжнародних електронних платежів.
Габріель є молода людина-підприємець з Ріо-Де-Жанейро, що утримує маленьку веб крамницю, що продає майки з надрукованим логотипом біткоіну, а також чашки та наліпки. Габріель дуже юний щоб мати банківський рахунок, але його батьки підтримують його підприємницький хист.
Євгенія є директором благодійного фонду на Філіпінах. Нещодавно вона відкрила біткоін, та бажає використати цілу нову групу закордонних та місцевих донорів для фундації власного фонду. Вона також досліджує шляхи для використання біткоіну для швидкого розподілу фондів до місцевосцей, де в них є потреба. Ця історія покаже використання біткоіну для глобального фінансування за межами валют та границь, та використання відкритого обліку для прозорості діяльності благодійних організацій.
Мохамед є імпортером електроніки в Дубаї. Він намагається використовувати біткоін для придбання електроніки зі Сполучених Штатів та Китаю для імпорту в Емірати, щоб пришвидшити процес платежів для імпортерів. Ця історія покаже, як біткоін може бути використаний для великих міжнародних платежів бізнес-до-бізнесу, що пов'язані з фізичними товарами.
Джинг є студентом комп'ютерного інжинірингу в Шанхаї. Він побудував “майнинговий” пристрій, щоб видобувати біткоін з використанням інженерних навичок, щоб отримати прибуток. Ця історія висвітлює "індустріальну" сторону біткоіну: спеціалізоване обладнання для унебезпечення мережі біткоіну, та випуску нової валюти.
Кожна з ціх історій базована на реальних людях та реальних галузях, що наразі використовують біткоін для створення нових ринків, нових галузей, та інновативних рішень проблем глобальної економіки.
Біткоін є протоколом, до якого можна отримати доступ з використанням клієнтського застосування, що розмовляє за цім протоколом. "Гаманець біткоіну" є найбільш загальним користувацьким інтерфейсом до системи біткоіна, так само, як переглядач є найбільш загальним користувацьким інтерфейсом до протоколу HTTP.
Існує багато реалізацій та брендів гаманців біткоіну, так само, як є багато брендів веб переглядачів (Chrome, Safari, Firefox, та Internet Explorer). Та так само, як ви маєте свій улюблений веб переглядач (Mozilla Firefox, так!), та наші негідники (Internet Explorer, ні!), гаманці біткоін різняться за якістю, продуктивністю, безпекою, приватністю та надійністю. Також є референсна реалізація протоколу біткоіну, що включає гаманець, відома як "Клієнт Сатоші", що походить від оригінальної реалізації, написаної Satoshi Nakamoto.
Гаманці біткоін є найбільш розроблювані застосування в екосистемі біткоін. Існує потужна конкуренція, та якщо новий гаманець буде розроблений прямо зараз, декілька з останнього року більше не отримують підтримки. Багато гаманців фокусуютсья на специфічних платформах, або специфічних використаннях, та деякі більш придатні для початківців, тоді як ініші перевантажені можливостями для досвідчених користувачів. Обирання гаманця дуже суб'єктивне, та залежить від його використання та кваліфікації користувача. Таким чином неможливо рекомендувати окремий бренд або проект гаманця. Однак ми можемо розкласти на категорії гаманці біткоіну, відповідно до платформи та функцій, та запровадити деяку ясність щодо всіх різних типів гаманців, що існують. Навіть краще, пересилання грошей між гаманцями біткоіну легке, дешеве та швидке, так що можна спробувати декілька різних гаманців, докі ви знайдете той, що задовільняє вашим потребам.
Гаманці біткоін можуть бути розбиті на категорії наступним чином, відповідно до платформи:
Десктопні гаманці були першим типом гаманців біткоін, створені як референсна реалізація, та багато користувачів використовують десктопні гаманці для можливостей, автономії та контролю, що вони надають. Однак їх виконання на операційних системах загального використання, таких, як Windows або Mac OS, мають декілька недоліків безпеки, бо ці платформи часто небезпечні та невірно сконфігуровані.
Мобільні гаманці є найбільш загальним типом гаманців біткоін. Виконуючись на операційних системах смартфонів, як Apple iOS та Android, ці гаманці часто є гарним вибором для користуваа. В значній мірі розроблені для простоти та зручності в користуванні, вони, тим не менш, повністю фукціональні гаманці для потужних користувачів.
Веб гаманці мають доступ через веб переглядач, та зберігають гаманець користувача на сервері, що належить третій стороні. Це подібно до веб пошти, коли ви повністю покладаєтесь на сервер. Деякі з ціх сервісів оперують, використовуючи код на боці клієнта, що використовується в переглядачі клієнта, що утримує контроль над ключами біткоіну в руках користувача. Однак більшість представляють компроміс, відбираючи в користувача контроль над ключами біткоіну, в обмін на простоту використання. Не можна рекомендувати зберігання великої кількості біткоіну на системах третіх сторін.
Апаратні гаманці є пристроями, що оперують як самодостатній гаманець біткоіну на базі спеціального апаратного обладнання. Вони роблять через USB на десктопних веб переглядачах, або через коротко-досяжні комунікації (NFC) на мобільних пристроях. Через обробку всіх біткоін операцій на спеціалізованому обладнанні, ці гаманці визнані дуже безпечними, та підходять для зберігання великих кількостей біткоін.
Ключі, що контролюють лбіткоін, також можуть бути роздруковані для довготривалого зберігання. Це відоме як паперові гаманці, навіть якщо можуть використовуватись інші матеріали (деревина, метал, тощо). Паперові гаманці пропонують низькотехнологічний, але дуже безпечний спосіб зберігання біткоіну на тривалий термін. Офлайн сховище часто посилаєтсья як холодне сховище.
Інший шлях категоризації гаманців біткоін є їхня ступінь автономності, та як вони взаємодіють з мережею біткоін:
Повний клієнт, або "повний вузол", це клієнт, що зберігає повну історію всіх транзакцій біткоін (кожну транзакцію для кожного користувача, будь-що), керує користувацькими гаманцями, та може ініціювати транзакції напряму в мережу біткоін. Повний вузол обробляє всі аспекти протоколу, та може незалежно перевіряти повний блокчейн, та кожну окрему транзакцію. Повно-вузловий клієнт споживає значні комп'ютерні ресурси (більше ніж 125Гб диску, 2Гб оперативної пам'яті), але пропонує повну автономію та незалежну верифікацію транзакцій.
Легковажний клієнт, також відомий як клієнт зі спрощеною перевіркою
платежів (simple-payment-verification, SPV),
під'єднується до повних вузлів біткоіну (зазначених вище) для
доступу до інформації щодо транзакцій, але зберігає гаманець користувача
локально, та незалежно створює, перевіряє та передає транзакції.
Легковажні клієнти напряму взаємодіють з мережею біткоін, без
посередників.
Клієнти з API третіх сторін взаємодіють з біткоіном через системи третіх сторін, через програмні інтерфейси (API), замість того, щоб напряму під'єднуватись до мережі біткоін. Гаманець може зберігатись користувачем або на серверах, але всі транзакції ідуть через посередників.
Комбінуючи ці категорізації, багато біткоін гаманців підпадають в декілька груп, де три найбільш загальніє є повний десктопний клієнт, мобільний легковажний клієнт та веб гаманець від третьої сторони. Межа між різними категоріям є досить розмитою, бо багато гаманців вміють виконуватись на декількох платформах, та можуть взаємодіяти з мережею в різний спосіб.
Для цілей цієї книжки ми будемо демонструвати використання різноманітних клієнтів, що можна завантажити, від референсної реалізації (Bitcoin Core), до мобільних та веб гаманців. Деякі з прикладів будуть потребувати Bitcoin Core, що на додаток до того, що це повний клієнт, також пропонує API до послуг гаманця, мережі, та транзакцій. Якщо ви плануєте дослідити програмні інтерфейси в екосистемі біткоін, вам знадобиться Bitcoin Core, або один з альтенативних клієнтів (дивіться "Альтернативні клієнти, бібліотеки та тулкіти").
Аліса, з якою мипознайомились раніше, не є технічним користувачем, та тільки нещодавно почула про біткоін від друга Джо. Перебуваючи на вечірці, Джо раз за разом натхненно пояснював ідею біткоіна всім докола нього, та пропонував зробити демонстрацію. Заінтригована, Аліса запитала, як вона може розпочати взаємодію з біткоін. Джо сказав, що мобільний гаманець найкращий для початківців, та рекомендував декілька з його улюблених гаманців. Аліса завантажила "Mycelium" для Android, та встановила його на свій телефон.
Потім Аліса запустила Mycelium в перший раз, та, як багато інших біткоін
гаманців, застосування автоматично створило новий гаманець для неї. Аліса
побачила свій гаманець на екрані, як показано на Малюнку 1-1 (зауваження:
не надсилайте біткоін до цієї фіктивної адреси, вони будуть втрачені
назавжди).
Малюнок 1-1. Мобільний гаманець Mycelium
Найбільш важлива частина на цьому екрані є біткоін адреса Аліси. На
екрані вона виглядає як довгий рядок літер та цифр:
1Cdid9KFAaatwczBwBttQcwXYCpvK8h7FK. Далі за адресою біткоіну в гаманці іде
QR код, певна форма бар-коду, що містить ту ж саму інформацію в форматі,
що може біти просканований камерою смартфона. QR код є квадратом з
шаблоном з чорних та білих крапок. Аліса може скопіювати адресу біткоін
або QR код в свій буфер обміну, клацнувши на QR коді, або на кнопці
Receive (Отримати). В більшості гаманців клацання на QR коді буде також
збільшувати його, так що вам може більш просто скануватись камерою
смартфона.
Адреса біткоіна починається з 1 або 3. Як адреси електронної пошти, вони можуть бути поділені з іншими користувачами біткоіну, які можуть використовувати їх для надсилання біткоінів прямо до гаманця. Тут немає нічого чутливого з точки зору безпеки, щодо адрес біткоіна. Він може бути опублікований будь-де, без ризику для безпеки рахунку. На відміну від поштової адреси, ви можете створити нову адресу так часто, як побажаєте, та всі вони будуть спрямовувати гроші в ваш гаманець. Фактично, багато сучасних гаманців автоматично створюють нові адреси для кожної транзакції, щоб максимізувати приватність. Гаманець просто колекція адрес та ключів, що відмикають суми з ціх адрес.
Тепер Аліса готова приймати платежі. Її застосування-гаманець випадково генерує приватний ключ (як описане в деталях в розділі "Приватні ключі"), разом з відповідними адресами біткоін. В цій точці її адреса біткоін не відома для мережі біткоін, або не "зареєстрована" будь якою стороною в системі біткоін. Її адреса біткоін просто число, що відповідає до ключа, за допомогою вона може отримати контроль за сумами на цій адресі. Ключ був згенерований незалежно гаманцем, без посилань або реєстрації жодним сервісом. Фактично, в більшості гаманців, немає асоціації між адресами біткоіну та жодною зовнішньою ідентифікуючою інформацією, включаючи дані про користувача. До того часу, як ця адреса буде використана як отримувач вартості в транзакції, що надіслана в реєстр біткоін, адреса біткоін є просто частиною загального числа можливих адрес, що є валідними в біткоін. Тількуи коли вона стає асоційованою з транзакцією, тільки тоді вона стає частиною адрес, що відомі мережі.
Наразі Аліса готова почати використовувати її новий біткоін гаманець.
Першим, та часто найбільш складним завданням для нових користувачів, є отримання деяких біткоінів. На відміну від інших валют, ви ще доки не можете придбати біткоіни в банку або в пункті обміну валют.
Транзакції біткоіну не мають зворотньої дії. Більшість мереж електронних
платежів, такі, як кредитні картки, PayPal, та банківські рахунки, мають
змогу відміни платежу. Для декого, хто продає біткоін, ця різниця додає
дуже великий ризик, що покупець поверне електронний платіж після отримання
біткоіну, тобто ошукає продавця. Щоб зменшити цей ризик, компанії, що
приймають традиційні електронні платежі в обмін на біткоін, зазвичай
потребують від покупців пройти перевірку особистості та
платежеспроможнсоті, що може зайняти декілька днів або тижнів. Як для
нового користувача, це означає, що ви не зможете придбати біткоін напряму,
за допомогою кредитної картки. За допомогою певної терплячості та
креативного мислення вам це і не знадобиться.
Ось декілька способів отримати біткоін для нових користувачів:
• Знайти товариша, який має біткоін, та купити в нього декільку суму
напряму. Багато користувачів біткоіну почали цім шляхом. Цей метод найменш
складний. Один зі способів познайомитись з людьми з біткоінами є завітати
та місцеву подію зі списку Meetup.com.
• Використати перевірений сервіс зі списку localbitcoins.com, щоб знайти
продавця в вашій місцевості, та купити біткоін за готівку при
безпоседерній транзакції.
• Заробити біткоін через продажу продуктів або послуг за біткоін. Якщо ви
програміст, продавайте ваші програмістські навички. Якщо ви перукар,
стрижить волосся за біткоін.
• Використовуйте автомати ATM біткоіну в вашому місці. Автомати біткоіну
є машиною, що приймає готівку, та надсилає біткоін на гаманець біткоін в
вашому смартфоні. Знайдіть найближчий до вас біткоін ATM з використанням
мапи від Coin ATM Radar.
• Використовуйте обмін валют на біткоін, пов'язаний з вашим банківськім
рахунком. Багато країн наразі мають обміни валют, що пропонують продавцям
та покупцям ринок продажу біткоін за місцеву валюту. Сервіси курсів обміну
валют, такі, як BitcoinAverage, часто показують перелік обмінників біткоін
для кожної з валют.
Одна з переваг біткоіну над інши платіжними системами є те, що коли застосована коректно, вона надає значно більшу приватність. Отримання, зберігання та витрата біткоіну не потребує від вас розголошення чутливої та персонально ідентифікуючої інформації третім сторонам. Однак там, де біткоін зачіпає традиційні системи, такі, як обмінники валют, часто застосовуются національні або міжнародні регулятивні норми. Щоб обміняти біткоін на вашу місцеву валюту, вам часто знадобиться запровадити доказ вашої особистості та надати банківську інформацію. Користувачі повинні бути попереджені, що як тільки адреса біткоін буде пов'язана з особистими даними, всі асоційовані транзакції біткоіну також буде легко ідентифікувати та відстежити. Це та причина, чому багато користувачів обирають обслуговувати окремі обмінні рахунки, не пов'язані з їх гаманцями.
Аліса війша в світ біткоін завдяки товаришу, так що вона пройшла простим шляхом для отримання прерших біткоінів. Далі ми побачимо, як вона куауватиме свої біткоіни у друга Джо, та як Джо надішле біткоіни до її гаманця.
Перед тим, як Аліса придбає перші біткоіни від Джо, вони мають домовитись щодо курсу обміну між біткоіном та доларами США. Це підіймає загальне запитання для новачків в біткоін: "Хто встановлює ціну біткоіна?". Коротка відповідь - ціну встановлює ринок.
Біткоін, як і інші валюти, має плаваючий обмінний курс. Це означає, що вартість біткоіну до кожної іншої валюти змінюється відповідно до пропонування та попиту на різних ринках, де він торгуєтсья. Наприклад, "ціна" біткоіна до долара США обчислюється на кожному з ринків, базуючись на останніх торгах біткоіна до долару. Я к така, ціна має тенданцію змінюватись щохвилини, по декілька разів на секунду. Сервіси цін будуть агрегувати ціни від декількох ринків, та обчислювати взважене за об'ємом середнє, що представлє обмінний курс валюти для певної пари (BTC/USD).
Існує сотні застосувань та веб сайтів, що можуть провадити поточні курси на ринку. Ось декілька найбільш популярних:
Сайт, що провадить простий погляд на взаважене за об'ємом середнє для кожної валюти.
Сервіс переліку капіталізації ринку та обмінних курсів для сотен крипто валют, включаючи біткоін.
Рівень посилань, що може використовуватись для інституційного або контрактного посилання, що провадиться як частина інвестиційних фідів від CME.
На додаток до ціх різноманітних сайтів та застосувань, більшість біткоін гаманців будуть автоматично конвертувати суми в біткоінах в інші валюти. Джо буде використовувати свій гаманець для автоматичної конвертації ціни, перед тим, як надіслати біткоін до Аліси.
Аліса вирішила обміняти $10 на біткоін, щоб не дуже ризикувати грошима з
новою технологією. Вона дає Джо $10 готівкою, відкриває свій
гаманець-застосування Mycelium, та обирає Отримати (Receive). Це висвічує
QR код з першою біткоін адресою Аліси. Потім Джо обирає Надіслати (Send)
на своєму смартфоні та потрапляє у вікно з двома полями:
• Цільова адреса біткоін
• Суму, що надіслати, в біткоінах (BTC) або в місцевій валюті (USD)
В полі вводу для адреси біткоін є мала іконка, що виглядає як QR код. Це
дозволяє Джо сканувати бар-код за допомогою камери смартфону, так що він
не має набирати адресу біткоін Аліси, що досить довга та складна для
вводу. Джо клацає по іконці QR, та активує камеру смартфона, скануючи QR
код, що висвітлюється на смартфоні Аліси.
Тепер Джо має адресу біткоін Аліси в якості отримувача. Джо вводить суму
$10, та гаманець конвертує її, отримуючи доступ до новітніх курсів обміну
від онлайн сервісу. Курс обміну на той час становить $100 за біткоін, так
що $10 вартує 0.10 біткоін (BTC), або 100 мілі біткоінів (mBTC), як
показано на екрані з гаманця Джо (Малюнок 1-2).
Малюнок 1-2. Екран надсилання мобільного гаманця Airbitz
Тепер Джо уважно все перевіряє, щоб переконатись, що він ввів коректну суму, оскільки він збираєтсья перевести гроші, та помилки не мають зворотньої ходи. Після подвійної перевірки він натискає Надіслати (Send), щоб надіслати транзакцію. Мобільний гаманець біткоін Джо будує транзакцію, що присвоює 0.10 BTC адресі, наданій від Аліси, знімаючи гроші з гаманця Джо, та підписуючи транзакцію приватним ключем Джо. Це каже мережі біткоін, що Джо авторизований переказати вартість до нової адреси Аліси. Коли транзакція передана через двосторонній протокол, вона швидко поширюється по мережі біткоін. Швидше ніж за секунду більшість гарно-під'єднаних вузлів в мережі отримають цю транзакцію, та в перший раз побачать адресу Аліси.
Тим часом, гаманець Аліси весь час "слухає" опубліковані транзакції в мережі біткоін, виглядачи на все, що співпадає з адресами в її гаманці. Через декілька секунд, після того, як гаманець Джо надіслав транзакцію, гаманець Аліси зафіксує, що отримав 0.10 BTC.
Зпочатку адреси Аліси будуть показувати транзакції Джо я к
непідтверджені (Unconfirmed). Це означає, що транзакція поширилась
мережею, але все ще не записана в реєстрі транзакцій біткоін, що в
середньому відбувається кожні 10 хвилин. В традиційних фінансових термінах
це відоме як очистка. Щодо додаткових деталей про розповсюдження,
валідацію та очистку (підтвердження) біткоін транзакцій дивіться Главу 10.
Тепер Аліса повновласний володар 0.10 BTC, які вона може витрачати. В
наступній главі ми побачимо її перше придбання за допомогою біткоін, та
дослідимо відповідну транзакцію та технологію розповсюдження більш
детально.
Система біткоін, на відміну від традиційних банків та платіжних систем, базується на децентралізованій довірі. Замість центральної довіреної установи, в біткоіні довіра досягаєтсья як неочевидна властивість від взаємодії різних приймаючих участь сторін в системі біткоін. В цій главі ми дослідимо біткоін на високому рівні, через відстеження поодинокої транзакції в системі літкоін, та побачимо, як вона стає "довіреною" та сприяється механізмом розподіленого консенсусу біткоін, та, нарешті, записується в блокчейн, розподілений реєстр всіх транзакцій. Наступні глави будуть занурюватись в технології позаду транзакцій, мережу та майнінг.
На оглядовій диаграмі, показаній на Малюнку 2-1, ми бачимо, що система біткоін складається з користувачів з гаманціми, що містять ключі, транзакції передаються мережею, та майнери, що продукують (через змагання в обчисленні) консенсус блокчейну, якій, загалом, є реєстром всіх транзакцій.
Кожний приклад в цій главі базуєтся на справжній транзакції, зробленій в
мережі біткоін, що симулює взаємодію між користувачами (Джо, Аліса, Боб та
Гопеш), через надсилання фондів з одного гаманця на інший. При відстеженні
трензакції по мережі біткоін до блокчейну, ми будемо використовувати
сайт-переглядач блокчейну, щоб візуалізувати кожний крок. Переглядач
блокчейну є веб застосуванням, що оперує як пошукова машина біткоіна, в
тому сенсі, що дозволяє шукати адреси, транзакції та блоки, та бачити
відношення та переходи між ними.
Популярні переглядачі блокчейну включають:
• Bitcoin Block Explorer
• BlockCypher Explorer
• blockchain.info
• BitPay Insight
Кожний з них має функції пошуку, що може сприймати адресу біткоін, хеш транзакції, номер блоку, або хеш блоку, та повертає відповідну інформацію з мережі біткоін. З кожною транзакцією або прикладом блоку, ми будемо провадити URL, так що ви можете побачити це самі та вивчити в деталях.
Аліса, з якою ми познайомились в попередній главі, є новим користувачем, що тільки отримала свій перший біткоін. В попередній главі вона зустрілась зі своїм товаришем Джо, щоб обміняти деяку готівку на біткоін. Транзакція, створена Джо, збагатила гаманець Аліси на 0.10 BTC. Тепер Аліса робить свою першу купівельну транзакцію, купуючи каву в кав'ярні Боба в Пало Альто, Каліфорнія.
Кав'ярні Боба нещодавно почала приймати платежі в біткоіні, через додавання опції біткоіну до своєї платіжної системи. Ціни позначені в місцевій валюті (доларах), але на касі споживачі мають опцію заплатити або доларами, або біткоінами. Аліса отримала свій рахунок за свою каву, та Боб додав його до журналу, як він робить з усіма транзакціями. Система точки продажу автоматично конвертує загал з доларів США в біткоін за поточним ринковим курсом, та відображує вартість в обох валютах:
Total:
$1.50 USD
0.015 BTC
Боб каже: "Це півтори долари або п'ятнадцять мілібіт". Система точки продажу Боба також автоматично створить окремий QR код, що міститиме запит на сплату (Малюнок 2-2). На відміну від QR коду, що просто містить цільову адресу біткоіну, запит на сплату є QR-кодованим URL, що містить цільову адресу, суму до сплати, та загальну інформацію, як "Bob’s Cafe". Це дозволяє гаманцю біткоін заповнити інформацію для сплати рахунку, при цьому показавши дані платежу користувачеві. Ви можете сканувати QR код за допомогою застосування біткоін гаманця, щоб побачити, що має побачити Аліса.
Малюнок 2-2. QR код платіжного запиту
Спробуйте сканувати цей код за допомогою вашого гаманця, щоб побачити адресу на суму, але НЕ НАДСИЛАЙТЕ ГРОШІ.
bitcoin:1GdK9UzpHBzqzX2A9JFP3Di4weBwqgmoQA?
amount=0.015&
label=Bob%27s%20Cafe&
message=Purchase%20at%20Bob%27s%20Cafe
Адреса біткоін: "1GdK9UzpHBzqzX2A9JFP3Di4weBwqgmoQA"
Сума платежу: "0.015"
Мітка щодо отримувача: "Bob's Cafe"
Опис (коментар) до платежу: "Purchase at Bob's Cafe"
Аліса використовує власний смартфон для сканування бар-коду, що
відображений. Її смартфон показує платіж на 0.0150 BTC до Bob’s Cafe, та
вона обирає надіслати платіж. За декілька секунд (приблизно за час
авторизації кредитної картки),
Боб бачить транзакцію в реєстрі, що завершує транзакцію.
В наступних розділах ми дослідимо транзакції більше детально. Давайте
зараз подивимось, як гаманець Аліси побудував її, як він поширив її в
мережі, як вона стала верифікована, та, нарешті, як Боб зміг витратити цю
суму в подальших транзакціях.
Мережа біткоін може обмінюватись частковими значеннями, від мілі-біткоінів (1/1000 біткоіна), аж до 1/100,000,000 від біткоіна, що відоме як сатоші. В цій книзі ми будемо використовувати термін "біткоін" для любої кількості валюти біткоін, від найменьших одиниць (1 сатоші) до загального числа (21,000,000) всіх біткоінів, що будь коли будуть видобуті.
Ви можете перевірити транзакцію Аліси до Bob’s Cafe в блокчейні,
викуористовуючи переглядач блокчену (Приклад 2-1):
Приклад 2-1. Перегляд транзакції Аліси на blockexplorer.com
https://blockexplorer.com/tx/
0627052b6f28912f2703066a912ea577f2ce4da4caa5a5fbd8a57286c345c2f2
В простих термінах, транзакція каже мережі, що власник деякої вартості біткоінів авторизовано передає цю вартість іншому власникові. Новий власник тепер може витратити біткоін для інших транзакцій, що авторизують передачі вартості іншим власникам. Новий власник тепер може витратити біткоін для іншої транзакції, що авторизує передачу до іншого власника, і так далі, по ланцюгу власників.
Транзакції подібні до рядків реєстру подвійної звітності. Кожна транзакція налічує один або більше "входів", що виступають як дебет відносно рахунку біткоіна. З іншого боку транзакції є один або більше "виходів", що виступають як кредити, додані до рахунку біткоін. Входи та виходи (дебіти та кредити) не обов'язково складають ту ж саму суму. Замість цього, виходи в сумі дещо менші, ніж входи, та різниця представляє призначені комісійні транзакції, що є малим платежем, що надходить до майнера, який включає транзакцію в реєстр. Транзакція біткоін показана як запис в бухгалтерській реєстр на Малюнку 2-3.
Транзакція також містить доказ власності для кожної суми в біткоін (входів), суми яких витрачаються, та формують цифровий підпис власника, що може бути незалежно перевірений будь-ким. В термінах біткоіну, "витрачання" є підпис транзакції, що пересилає вартість від попереднього власника транзакції до нового власника, ідентифікованого адресою біткоін.
Малюнок 2-3. Транзакція як запис за подвійною звітністю.
Платіж Аліси до Bob’s Cafe використовує попередні виходи транзакцій як
входи. В попередній главі, Аліса отримала біткоіни від її товариша Джо, в
обмін на готівку. Ця транзакція створила вартість біткоін, що закріплена
за ключем Аліси. Її нова транзакція до кав'ярні Боба посилається на
попередню транзакцію як на вхід, та створює нові виходи, щоб сплатити за
каву, а також отримати решту. Транзакції утворюють ланцюг, де входи від
останніх транзакцій відповідають виходам від попередніх транзакцій. Ключ
Аліси провадить сигнатуру (цифровий підпис), що відмикає ці виходи
попередніх транзакцій, таким чином запевняючи мережу біткоін, що вона є
власником ціх фондів. Вона приєднує платіж за каву до адреси Боба, таким
чином "ускладнюючи" цей вихід тією умовою, щоб Боб зпродукував сигнатуру,
щоб витратити цю суму. Це і є передача вартості від Аліси до Боба. Цей
ланцюг транзакцій, від Джо до Аліси, та від Аліси до Боба, проілюстрований
на Малюнку 2-4.
Малюнок 2-4. Ланцюг з транзакцій, де вихід з однієї транзакції є входом
для наступної транзакції
Багато транзакцій біткоін будуть включати виходи, що посилаються на обоє, адресу нового власника, та на поточного власника, що називається адресою решти. Це так, бо входи транзакцій, як і банкноти, не можуть бути поділені. Якщо ви купляєте на суму $5, але надаєте купюру $20, ви очікуєте значу в розмірі $15. Та ж концепція застосовується до входів транзакції біткоін. Якщо ви придбаєте дещо вартістю 5 біткоінів, але маєте на вході тільки 20 біткоінів, що можна витратити, ви маєте надіслати один вихід в 5 біткоінів до власника крамниці, та один вихід в 15 біткоінів назад до себе, як решту (зменшивши суму на достатні комісійні з транзакції).
Важливо, що адреса для решти не була тою самою адресою, що є на вході, та з причин приватності часто це нова адреса з гаманця власника.
Різні гаманці можуть використовувати різні стратегії при накопичуванні
входів, щоб зробити платіж на вимогу користувача. Вони можуть агрегувати
багато малих входів, або використовувати один, що рівний або більший, ніж
бажаний платіж. Якщо тільки гаманець не може підібрати входи в такий
спосіб, щоб точно співпасти з бажаним платежем плюс комісійні, гаманець
потребуватиме згенерувати деяку решту. Це дуже подібне до того, що люди
роблять з готівкою. Якщо ви завжди використовуєте найбільшу купюру з вашої
кишені, ви скінчите з повними карманами решти. Якщо ви використовуєте
тільки роздріб зі решти, у вас залишаться лише крупні купюри. Люди
підсвідомо знаходять баланс між ціма двома крайнощами, та розробники
біткоін гаманців намагаються запрограмувати цей баланс.
Підсумовуючи, транзакції пересувають вартість від входів транзакції до виходів транзакцій. Вхід посилаєтся на вихід попередньої транзакції, показуючи, звідки походить вартість. Вихід транзакції спрямовує вказану вартість на адресу нового власника, та може включати решту, що надходить назад до попереднього власника. Виходи від однієї транзакції можуть бути використані як входи в новій транзакції, таким чином створюючи ланцюг з власників, по мірі того, як вартість пересувається від власника до власника (дивіться Малюнок 2-4).
Найбільш загальною формою транзакцій є прості платежі від однієї адреси до іншої, що часто включає деяку "решту", що повертається початковому власнику. Цей тип транзакцій має один вхід та два виходи, як показано на Малюнку 2-5.
Малюнок 2-5. Найбільш загальна транзакція
Інша загальна форма транзакції є така, що агрегує (збирає) декілька
входів в один вихід (дивіться Малюнок 2-6). Це представляє еквівалент з
реального світу розміну груди монет та купюр на одну велику банкноту.
Транзакції, подібні до цієї, іноді генеруються застосуванням гаманця, щоб
очистити массу менших сум, що отримані як решти з платежів.
Малюнок 2-6. Транзакція, що збирає фонди
Нарешті, ще одна форма транзакції, що часто можна бачити в реєстрі біткоіну, є транзакція, що розпорошує один вхід на багато виходів, що представляють багато отримувачів (дивіться Малюнок 2-7). Цей тип транзакцій часом використовується комерційними засадами для розподілення фондів, таких, як при обробці виплат заробітної платні багатьом співробітникам.
Малюнок 2-7. Транзакція з розпорошення фондів
Застосування-гаманець Аліси містить всю логіку для вибору відповідних входів та виходів, щоб побудувати транзакцію за вимогами Аліси. Алісі тільки треба вказати призначення та суму, та загал відбувається в застосуванні гаманця, без того, щоб вона бачила деталі. Важливим є те, що застосування-гаманець може будувати транзакції, навіть якщо він повністю в офлайні. Так само, як написання чеку вдома, та подальше надсилання його до банку в конверті, транзакція не має бути сконструйована та підписана, доки ви під'єднані до мережі біткоін.
Застосування-гаманець Аліси зпочатку має знайти входи, що можуть сплатити суму, яку вона бажає надіслати Бобу. Більшість гаманців будуть відстежувати всі доступні виходи, що належать адресам, керованим гаманцем. таким чином, гаманець буде містити копію виходів транзакцій від транзакції Джо, що була утворена через обмін на готівку (дивіться "Отримання ваших перших біткоінів"). Застосування гаманця біткоін, яке виконуєтсья як повний клієнт, насправді містить копію всіх виходів для кожної транзакції в блокчейні. Це дозволяє гаманцю будувати входи транзакцій, так само, як швидко перевіряти надходячі транзакції, що вони мають коректні входи. Однак, оскільки повний вузол займає багато дискового простору, більшість користувачів виконують "легковажні" клієнти, що відстужують тільки власні невитрачені виходи користувача.
Якщо застосування-гаманець не відстежує копію невитрачених виходів
транзакцій, воно може запитати мережу біткоін, щоб отримати цю інформацію
з використанням різних API, доступних через різних провайдерів, або через
запит до повних вузлів, використовуючи виклики програмного
інтерфейсу(API). Приклад 2-2 показує запит API, побудований як команда
HTTP GET для специфічного URL. Цей URL поверне всі невитрачені транзакції
для наданої адреси, надаючи кожному застосуванню інформацію, яка потрібна
для побудови входів для витрати. Ми використовуємо простий клієнт HTTP
командного рядка, cURL, для отримання відповіді.
Приклад 2-2. Перегляд всіх невитрачених виходів для біткоін адреси Аліси
$ curl https://blockchain.info/unspent?active=1Cdid9KFAaatwczBwBttQcwXYCpvK8h7FK
{
"unspent_outputs":[
{
"tx_hash":"186f9f998a5...2836dd734d2804fe65fa35779",
"tx_index":104810202,
"tx_output_n": 0,
"script":"76a9147f9b1a7fb68d60c536c2fd8aeaa53a8f3cc025a888ac",
"value": 10000000,
"value_hex": "00989680",
"confirmations":0
}
]
}
Відповідь в Прикладі 2-2 показує один невитрачений вихід (один, що ще не був відчинений), яким володіє адреса Аліси, 1Cdid9KFAaatwczBwBttQcwXYCpvK8h7FK. Відповідь включає посилання на транзакцію, що містить цей невитрачений вихід (платіж від Джо), та його вартість в сатоші, 10 мільйонів, що дорівнює 0.10 біткоін. Маючи ці інформацію, гаманець Аліси може побудувати надсилання цієї вартості на адресу нового власника.
Як ви можете бачити, гаманець Аліси містить досить біткоінів в одному
невитраченому виході, щоб сплатити за каву. Якби це не було так,
застосування-гаманець Аліси мав би "обшукувати" гору меньших невтрачених
виходів, як шукаються монети по карманах, докі не знайдеться сума на каву.
В обох випадках, може виникти потреба отримати щось в решту, як ми
побачимо в наступних розділах, по мірі того, як застосування-гаманець
створюватиме виходи транзакції (платежі).
Виходи транзакції створюються в формі скрипту, що створює перешкоду в вигляді значення, та може бути відчинений тільки через надання рішення до скрипта. Кажучи простіше, вихід транзакції Аліси буде містити скрипт, що каже щось подібне до такого: "Цей вихід може бути сплачений будь-ким, хто зможе представити сигнатуру від ключа, що відповідає публічній адресві Боба". Оскільки тільки Боб має гаманець з ключами, що відповідають цій адресі, тільки гаманець Боба може надати таку сигнатуру, щоб відчинити вихід. Аліса, таким чином,"обтяжує" значення виходу вимогою, щоб відкрити його за допомогою сигнатури від Боба.
Ця транзакція також буде містити інший вихід, бо на рахунку Аліси є вихід в 0.10 BTC , що забагато грошей за каву вартістю 0.015 BTC. Аліса має отримати 0.085 BTC решти. Платіж решти Аліси створюється гаманцем Аліси, як вихід до тої самої транзакції, що і платіж до Боба. Загалом гаманець поділяє накопичення Аліси на два платежі: один до Боба, та інший знову собі. Вона може потім використати (витратити) решту в наступній транзакції.
Нарешті, щоб транзакція була оброблена мережею в прийнятний час, гаманець Аліси додасть невеликі комісійні. Їх наочно не видно в транзакції, вони розуміються як різниця між входами та виходами. Якщо не брати решту в 0.085, Аліса створить тільки 0.0845 на другому виході, та залишить "на чай" 0.0005 BTC (половину мілі-біткоіну). Вхід в 0.10 BTC не повністю витрачений двома виходами, оскільки разом вони складають менше ніж 0.10. Отримана різниця є комісійні за транзакцію, що збираєтсья майнером як комісійні за валідацію та включення транзакції в блок, що буде записаний в блокчейн.
Результуюча транзакція може бути переглянута переглядачем блокчейну в веб застосуванні, як показано на Малюнку 2-8.
Малюнок 2-8. Транзакція Аліси до Bob’s Cafe
Витратьте час, та перегляньте цю транзакцію Аліси до Bob’s Cafe.
Транзакція, створена гаманцем Аліси, має 258 байтів за розміром, та містить все необхідне для підтверження прав власності над фондами, та призначення нового власника. Тепер транзакція має бути поширена в мережі біткоін, де вона має стати частиною блокчейна. В наступному розділі ми побачимо, як транзакція стає частиною нового блоку, та як цей блок "видобувається" (майниться). Нарешті, ми побачимо, як цей новий блок, один раз доданий до блокчейну, збільшує власну довіру з боку мережі, по мірі додавання нових блоків.
Оскільки транзакція містить всю інформацію, необхідну для обробки, не має значення, як та коли вона надійде до мережі біткоін. Мережа біткоін є мережею сторона-до-сторони, де кожний клієнт біткоін приймає участь через під'єднання до декількох інших клієнтів біткоін. Призначенням мережі біткоін є розповсюдження (просування) транзакцій та блоків між всіма зацікавленими сторонами.
Люба система, така як сервер, десктопне застосування, або гаманець, що приймає участь в мережі біткоін, та "розмовляє" по біткоін протоколу, називаєтсья вузлом біткоін. Застосування гаманця Аліси може надсилати нові транзакції до любого вузла біткоін, до якого воно під'єднане через любе з'єднання: дріт, WiFi, мобільний, тощо. Її гаманець біткоін не має бути підключений до гаманця біткоін Боба напряму, та вона не має використовувати інтернет з'єднання в кафе, хоча ці обоє варіанти також можливі. Любий вузол біткоін, що отримує валідну транзакцію, яку він до цього не бачив, має безпосередньо передати її всім іншим вузлам, до яких він під'єднаний. Ця техніка просування відома як фладінг (наводнення). Таким чином, транзакція швидко просувається по двосторонній мережі, досягаючи великого відсотка вузлів за декілька секунд.
Якщо застосування гаманця Боба напряму з'єднане з застосуванням гаманця Аліси, застосування гаманця Боба може бути першум вузлом, що отримає транзакцію. Однак навіть якщо гаманець Аліси надсилає транзакцію через ініші вузли. вона досягне гаманця Боба через декілька секунд. Гаманець Боба безпосередньо ідентифікує транзакцію Аліси як вхідний платіж, оскільки він містить вихід, що декодуєтсья ключами Боба. Застосування гаманця Боба також може безпосередньо перевірити, що транзакція гарно сформована, використовує попередньо невитрачені входи, та містить достатньо комісійних за транзакцію, щоб бути включеною в наступний блок. В цій точці Боб може вважати, з невеликим ризиком, що транзакція буде скоро включеною в блок та підтвердженою.
Загальне непорозуміння щодо транзакцій біткоіну є те, що вони мають отримати "підтвердження" через очікування 10 хвилин за новим блоком, або 60 хвилин для повних шести підтверджень. Хоча підтвердження гарантують, що транзакція була сприйнята всією мережою, така затримка не є необхідною для невеликих сум, таких, як купівля кави. Продавець може прийняти валідну транзакцію на невелику суму без підтверджень, з не більшим ризиком, ніж платіж кредитною карткою без ID або підпису, які сьогодні приймають всі торгівці.
Тепер транзакція Аліси розповсюджується мережею біткоін. Вона не стала частиною блокчейна, доки вона не перевірена та включена в блок, завдяки процесу, що відомий як майнинг. Дивіться Главу 10 щодо детальних пояснень.
Система довіри біткоін базується на обчисленнях. Транзакції складаються в блоки, які потребують неймовірної кількості обчислень, щоб мати доказ валідності, але тільки малої кількості для перевірки, що вони валідні. Процес майнингу прислуговуєтсья двом цілям в біткоін:
• Майнінгові вузли перевіряють всі транзакції через правила консенсусу
біткоіна. Таким чином, майнінг провадить безпеку для транзакцій біткоіна
через відхиляння невалідних або зловмисних транзакцій.
• Майнінг створює новий біткоін в кожному блоці, майже так, як центральний банк друкує нові гроші. Кількість біткоіну, створена в кожному блоці, обмежена та зменшується з часом, слідуя за розкладом фіксованого випуску.
Майнинг досягає гарного балансу між вартістю та винагородою. Майнинг використовує електрику для вирішення математичної проблеми. Успішний майнер буде збирати винагороди в формі нових біткоінів та комісійних від транзакцій. Однак збирання нагород буде відбуватись тільки якщо майнер буде коректно перевіряти всі транзакцї, що вони відповідають правилам консенсусу. Цей нав'язаний баланс провадить безпеку для біткоіна без центральної установи.
Гарним шляхом описати майнинг є гігантська змагальна гра в судоку, що скидається кожного разу, коли дехто знаходить рішення, та чия складність автоматично підлаштовується, так, щоб дехто знаходив рішення кожні 10 хвилин. Уявіть гігантську судоку, з декількома тисячами стовбчиків та рядків. Якщо я покажу вам готове рішення, ви можете швидко перевірити його досить швидко. Але якщо пазл має заповненими декілька клітин, та інше порожнє, рішення має зайняти багато роботи! Складність судоку може бути налаштована зміною розміру (більше або менше рядків та стовпчиків), але вона може бути перевірена досить просто, навіть якщо поле дуже велике. "Пазл", що використовується в біткоіні, базуєтся на криптографічному хеші, та має подібні характеристики: він асиметрично складний до розв'язання, та простий для перевірки, та його складність може бути налаштована.
Раніше ми познайомились з Джингом, підприємцем з Шанхаю. Джинг побудував майнингову ферму, що є бізнесом, де задіяні тисячі спеціалізованих майнингових комп'ютерів, що змагаются за винагороду. Кожні 10 хвилин, або близько до цього, майнингові комп'ютери Джинга змагаютсья з тисячами подібних систем в глобальних перегонагх за пошук рішення для блока транзакцій. Пошук такого рішення, так званий доказ виконаної роботи, Proof-of-Work (PoW), потребує квадрільйонів операцій в секунду по всій мережі біткоін. Алгоритм Proof-of-Work включає постійне хешування заголовку блока, та випаадкового числа, за допомогою крипторафічного алгоритма SHA256, докі рішення не співпаде з заздалегідь визначеним шаблоном. Перший майнер, що знайде таке рішення, виграє раунд, та публікує цей блок в блокчейні.
Джинг почав майнинг в 2010, використовуючи дуже швидкий десктоп для пошуку Proof-of-Work для нових блоків. По мірі того, як нові майнери почали долучатись до мережі біткоін, складність проблеми швидко зросла. Скоро Джинг та інші майнери перейшли на більш скеціалізоване обладнання, таке, як високо-потужні графічні карти (GPU), такі, що використовуютьсяв ігрових десктопах та консолях. На час написання цього абзацу складність стала такою високою, що майнинг залишається прибутковим лише на спеціальних інтегрованих пристроях (ASIC), де сотні майнингових алгоритмів видруковані в залізі, що роблять паралельно на одному кремнієвому чипі. Компанія Джинга також приймає участь в майнинговому пулі, що подібний до лотерейного пула, що дозволяє декільком учасникам розділити зусилля та винагороду. Компанія Джинга тепер скалає обчислювальний центр, що містить тисячі ASIC майнерів для добування біткоіну 24 години на добу. Компанія сплачує за електрику, через продаж біткоіну, що генерується від майнингу, створюючи деякі надходження від прибутків.
Нові транзакції постійно надходять до мережі від користувацьких гаманців та інших застосувань. По мірі того, як вузли бачать їх, вони додаются до тимчасового пулу неверифікованих транзакцій, що підтримуєтся кожним вузлом. Коли майнери конструюють новий блок, вони додають неперевірені транзакції з цього пулу до нового блоку, та потім намагаются довести валідність нового блока за допомогою майнінгового алгоритму (Proof-of-Work). Процес майнинга пояснений в Главі 10.
Транзакції, що додаються до нового блоку, приоритезуються за сплаченими комісійними, та декількома іншими критеріями. Кожний майнер починає процес майнингу нового блока транзакцй, як тільки він отримує попередній блок з мережі, що повідомляє його, що він програв попередній раунд змагання. Він зразу ж створює новий блок, заповнює його транзакціями, та ставить мітку попереднього блоку, та починає обчислювати доказ виконаної роботи, Proof-of-Work, для нового блока. Кожний майнер включає особливу транзакцію в свій блок, що сплачує на його власну адресу біткоін винагороду за блок (наразі 12.5 новостворених біткоінів), плюс суму з комісійних за всі транзакції, включені в блок. Якщо він знаходить рішення, що робить блок валідним, він "виграє" винагороду, оскільки його успішний блок додаєтся до глобального блокчейну, та транзакція-вианагорода стає витратною.
Джинг, який приймає участь в майнинговому пулі, встановив своє програмне забезпечення, що створює нові блоки, які надсилають винагороду на адресу пулу. З цього часу частина винагороди розподіляється на Джинга та інших майнерів, пропорційно до кількості роботи, які вони витратили в останньому раунді.
Транзакція Аліси була підхоплена мережею та включена в пул неперевірених (неверифікованих) транзакцій. Коли вона була валідована майнинговим програмним забезпеченням, вона стає включеною в новий блок, що згенерований майнинговим пулом Джинга. Всі майнери, що приймають участь в майниновому пулі, безпосередньо починають обчислення Proof-of-Work для блока-кандидата. Приблизно через п'ять хвилин, після того, як транзакція Аліси була передана гаманцем Аліси, один з ASIC майнерів Джинга знайшов рішення для блока-кандидати, та анонсував це в мережі. Коли інші майнери перевірили переможний блок, вони починають перегони за генерацію наступного блока.
Переможний блок Джинга стає частиною блокчпейна як блок 277316, та містить 420 транзакцій, включаючи транзакцію Аліси. Блок, що містить транзакцію Аліси, рахується як одне "підтвердження" цієї транзакції. Ви можете бачити блок, що включає транзакцію Аліси.
Приблизно через 19 зхвилин пізніше новий блок, 277317, видобуваєтсья іншим майнером. Оскільки цей блок побудований на основі блоку 277316, що містить транзакцію Аліси, він додає навіть більше обчислень до блокчейна, таким чином підсилюючи довіру до ціх транзакцій. Кожний блок, побудований на тому, що містить транзакцію, разується як додаткове підтвердження для транзакції Аліси. По мірі того, як блоки накопичуються один на одному, стає експоненціально складнішим відкатити транзакцію, так що вона стає все надійнішою з боку зору мережі.
Діаграма на Малюнку 2-9 показує блок 277316, що містить транзакцію Аліси. Нижче є 277,316 блоків (включаючи блок #0), пов'язані один з одним в ланцюг блоків (блокчейн), далі і далі до блоку 0, відомий як блок творення.
З часом "висота" блоків збільшується, так само як складність обчислення для кожного блока, та ланцюга загалом. Блоки, добуті після того, що містить абісину транзакцію, служать для додаткового переконання, бо вони грунтуються на все більших обчисленнях, в все більшому ланцюгу. За домовленостю, кожний блок, що має більше ніж шість підтверджень, розглядаєтся як неспростовний, оскільки він потребує неможливої кількості обчислень для відкликання та переобчислення шести блоків. Ми будемо вивчати процес майнінгу, та те, як він побудовує довіру, більш детально в Главі 10.
Малюнок 2-9. Транзакція Аліси, включена в блок #277316
Тепер, коли транзакція Аліси була вбудована в блокчейн як частина блоку, вона стала частиною розподіленого реєстру біткоіна, та видимою для всіх застосувань біткоіна. Кожний клієнт біткоіна може незалежно перевірити транзакцію, як валідну та витратну. Повні клієтни можуть відстежити джерело фондів від моменту, коли біткоін був зпочатку згенерований в блоці, поступово, від транзакції до транзакції, доки вони не досягнуть адреси Боба. Легковажні клієнти можуть зробити те, що називаєтся спрощеною верифікацією платежів (дивіться Спрощена верифікація платежів, SPV), через підтвердження, що транзакція знаходиться в блокчейні, та має декілька блоків після цього, таким чином провадячи доказ, що майнери сприйняли її як валідну.
Тепер Боб може витрачати вихід від цієї, та інших, транзакцій. Наприклад, Боб може сплатити контрактору або постачальнику, передавши вартість від платежу Аліси за каву цім новим володарям. Більш вірогідно, програмне забезпечення Боба буде збирати багато малих платежів в більший платіж, можливо, концентруючи всі щоденні надходження біткоіну в одну транзакцію. Таким чином можна зібрати всі різні платежі в один вихід (на одну адресу). Щодо діаграми агрегуючої транзакції дивіться Малюнок 2-6.
Коли Боб витрачає платежі, отримані від Аліси та інших клієнтів, він
продовжує ланцюг з транзакцій. Давайте вважати, що Боб сплачує своєму веб
дизайнеру Гопешу з Банглора за нову сторінку веб сайту. Тепер ланцюг з
транзакцій буде виглядати як Малюнок 2-10.
Малюнок 2-10. Транзакція Аліси як частина ланцюга транзакцій від Джо до
Гопеша
В цій главі ми побачили, як транзакції будують ланцюг, що пересуває
вартість від власника до власника. Ми також прослідили транзакцію Аліси,
від моменту, коли вона була створена в її гаманці, по мережі біткоін, та
до майнерів, які записали її в блокчейн. Далі в цій книзі ми будемо
досліджувати специфічні технології, що стоять за гаманцями, сигнатурами,
транзакціями, мережею, та, нарешті, майнингом.
Біткоін є проектом з вікритим кодом, та доступний під відкритою ліцензією (MIT), вільний до завантаження та для використання в любих цілях. Вікритий джерельний код означає більше, ніж просто вільне використання. Це також означає, що біткоін розроблений відкритою спільнотою волонтерів. З початку ці волонтери складались тільки з Satoshi Nakamoto. В 2016мц році первинний код біткоін мав більше ніж 400 контриб'ютерів з майже дюжиною розробників, що працювали над кодом майже повний час, та набагато більше, що працювали на неповному часі. Будь-хто може докластись до створення коду, включаючи вас!
Коли біткоін був створений Satoshi Nakamoto, програмне забезпечення було насправді завершене перед тим, як був створений опис, наданий в Додатку A. Satoshi бажав переконатись, що воно робить, перед тим, як писати про нього. Ця перша реалізація, відома як “Bitcoin” або “клієнт Satoshi”, була значно модифікована та покращена. Вона еволюціонувала в те, що зараз відоме як Bitcoin Core, щоб відрізіняти її від інших сумісних реалізацій. Bitcoin Core є референсною реалізацією системи біткоіну, що означає, що вона є авторитетним посиланням на кожну частину цієї технології, та як вона має бути реалізована. Bitcoin Core реалізує всі аспекти біткоіну, включаючи гаманець, рушій транзакцій та валідації блоків, та повний мережевий вузол в двосторонній мережі біткоін.
Не зважаючи на факт, що Bitcoin Core включає референсну реалізацію
гаманця, це не призначено для використання в якості промислового гаманця
для користувачів або для застосувань. Розробникам застосувань радиться
будувати гаманці з використанням сучасних стандартів, таких, як BIP-39 та
BIP-32 (дивіться “Мнемонічні кодові слова (BIP-39)” та “HD
гаманці (BIP-32/BIP-44)”). BIP означає Bitcoin Improvement Proposal.
Малюнок 3-1. Архитектура Bitcoin Core (Джерело:
Eric Lombrozo)
Якщо ви розробник, ви маєте бажати встановити
оточення розробки, з усіма інструментами, бібліотеками та підтримуючим
програмним забезпеченням для написання програм біткоін. В цій дуже
технічній главі ми крок за кроком пройдемо цей процес. Якщо матеріал
стане дуже щільним (та ви насправді не налаштовуєте оточення для
розробки), почувайтесь вільним пропустити залишок до наступної статті,
що є менш технічною.
Джерельний код Bitcoin Core може бути завантажений як архів ZIP, або клонуванням репозиторія коду з GitHub. На GitHub сторінці біткоін, оберіть Download ZIP з бокового меню. Альтернативно, використовуйте командний рядок та git для створення локлаьної копії джерельного коду в вашій системі.
В багатьох прикладах в цій главі ми будемо використовувати інтерфейс
командного рядка операційної системи (також відомий як “оболонка”), до
якого відбувається доступ через застосування “терміналу”. Оболонка буде
відображувати підказку; ви набираєте команду, та оболонка буде відповідати
деяким текстом та новою підказкою для вашої нової команди. Підказка може
виглядати інакше для вашої системи, але в наступних прикладах вона буде
позначатись як символ $. В ціх прикладах, коли ви бачите текст після
символа $, не друкуйте символ $, але друкуйте команду, що слідує за цім
символом, потім тисніть Enter для виконання команди. В прикладах, під
рядками кожної команди розташовані відповіді операційної системи на цю
команду. Коли ви бачите наступний префікс $, ви будете знати, що це інша
команда, та ви продовжуєте обробку.
В цьому прикладі ми використовуємо команду git для створення локальної копії (“клону”) джерельного коду:
$ git clone https://github.com/bitcoin/bitcoin.git
Cloning into 'bitcoin'...
remote: Counting objects: 66193, done.
remote: Total 66193 (delta 0), reused 0 (delta 0), pack-reused 66193
Receiving objects: 100% (66193/66193), 63.39 MiB | 574.00 KiB/s, done.
Resolving deltas: 100% (48395/48395), done.
Checking connectivity... done.
$
Git є найбільш широко використованої розподіленої системи контролю версій, однієї з основних інструментів розробника програмних застосувань. Вам може знадобитись встановити команду git, або графічний користувацький інтерфейс для git, в вашій операційній системі, якщо ви ще не маєте його.
Коли команда клонування git завершиться, ви матимете повну локальну копію джерельного коду репозитарія в каталозі bitcoin. Перейдіть в цей каталог, набравши наступну камонду в відповідь на підказку:
$ cd bitcoin
По замовчанню, локальна копія буде синхронізована з найбільш новим
кодом, що може бути нестабільною або бета версією біткоіна. Перед
компіляцією кода можна обрати іншу версію через вибір тегу релізу. Це
дасть можливість локальну копію з окремим станом репозитарію коду, що
ідентифікуєтсья ключовим тегом. Теги використовуються розробниками, щоб
відмітити особливі релізи коду через номери версій.
Зпершу, знайдіть всі теги, використовуючи команду git
tag:
$ git tag
v0.1.5
v0.1.6test1
v0.10.0
...
v0.11.2
v0.11.2rc1
v0.12.0rc1
v0.12.0rc2
...
Перелік тегів показує всі релізи версій біткоін.
За домовленостю реліз-кандидати, що призначені для тестування, мають
суфікс “rc”. Стабільні релізи, що
можуть виконуватись на промислових системах, не мають суфіксу. З
попереднього списку, оберіть найвищу версію релізу, що на час написання
була v0.11.2. Щоб синхронизувати локальний код з цією версіює,
використавуйте команду git checkout:
$ git checkout v0.11.2
HEAD is now at 7e27892... Merge pull request #6975
Ви можете підтвердити, що ви маєте бажану версію
“відміченою”, через команду git
status:
$ git status
HEAD detached at v0.11.2
nothing to commit, working directory clean
Первинний код містить документацію, що може бути знайдена в декількох файлах. Огляд головної документації розміщений в README.md в директорії bitcoin, який можна передивитись, набравши more README.md на підказку, та використовуючи клавішу проміжку для пересування на наступну сторінку. В цій главі ми побудуємо клієнт біткоін командного рядка, також відомий як bitcoind, на Linux. Передивіться інструкції щодо компіляції клієнта командного рядка bitcoind на вашій платформі, набравши more doc/build-unix.md. Альтернативні інструкції для macOS та Windows можуть бути ззнайдені в директорії doc, як build-osx.md або build-windows.md, відповідно.
Уважно передивіться передумови побудови, що є першою частиною документації. Ці бібліотеки мають бути присутні в системі, перед тим, як ви почнете будувати біткоін. Якщо ці передумови відсутні, процес побудови схибить з помилкою. Якщо це трапиться через те, що ви випустили передумову, ви можете встановити її, та потім продовжити процес побудови, там, де ви його лишили. Вважаючи, що ви встановили передумови, ви починаєте процес побудови, генеруючи скрипти, через використання скрипту autogen.sh.
Процес побудови Bitcoin Core були змінені, що
використовувати систему autogen/configure/make, починаючи з версії 0.9.
Старіші версії використовували простий Makefile, та роблять трохи інакше
від наступного приклада. Наступні інструкції для версій, що ви будете
компілювати. Введені autogen/configure/make, що з'явились в версії 0.9,
здається будуть використовуватись для всіх майбутніх версій кода, та ця
система демонструється в наступних прикладах.
$ ./autogen.sh
...
glibtoolize: copying file 'build-aux/m4/libtool.m4'
glibtoolize: copying file 'build-aux/m4/ltoptions.m4'
glibtoolize: copying file 'build-aux/m4/ltsugar.m4'
glibtoolize: copying file 'build-aux/m4/ltversion.m4'
...
configure.ac:10: installing 'build-aux/compile'
configure.ac:5: installing 'build-aux/config.guess'
configure.ac:5: installing 'build-aux/config.sub'
configure.ac:9: installing 'build-aux/install-sh'
configure.ac:9: installing 'build-aux/missing'
Makefile.am: installing 'build-aux/depcomp'
...
Скрипт autogen.sh
створює набір
автоматичних скриптів конфігурації, що будуть досліджувати вашу систему,
щоб винайти коректні налаштування, та переконатись, що присутні всі
потрібні бібліотеки для компіляції коду. Найбільш важливим з них є
скрипт configure, що пропонує декілька різних
опцій, щоб налаштувати процес побудови.
$ ./configure --help
`configure' configures Bitcoin Core 0.11.2 to adapt to many kinds of systems.
Usage: ./configure [OPTION]... [VAR=VALUE]...
...
Optional Features:
--disable-option-checking ignore unrecognized --enable/--with options
--disable-FEATURE do not include FEATURE (same as --enable-FEATURE=no)
--enable-FEATURE[=ARG] include FEATURE [ARG=yes]
--enable-wallet enable wallet (default is yes)
--with-gui[=no|qt4|qt5|auto]
...
Скрипт configure дозволяє вам ввімкнути або вимкнути певні можливості bitcoind через використання флагів --enable-FEATURE та --disable-FEATURE, де FEATURE замінюється на назву можливості, як зазначено в виводі допомоги. В цій главі ми будемо будувати клієнт bitcoind з усіма налаштуваннями по замовчанню. Ми не користуємось флагами конфігурації, але ви повинні переглядати їх, щоб розуміти, які опціональні частини є частиною клієнта. Якщо ви знаходитесь в академічному середовищу, обмеження комп'ютерної лабораторії можуть вимагати від вас встановлювати застосування в вашу домашню директорію (використовуючи --prefix=$HOME).
Ось деякі корисні опеції, що перекривають поведінку по замовчанню
скрипта конфігурації:
--prefix=$HOME Це перекриває місце інсталяції по замовчанню (/usr/local/) для результуючого виконавчого файлу. Використовуйте $HOME, щоб розмістит все в домашній директорії, або по іншому шляху.
--disable-wallet Це використовується для відключення реалізації референсного гаманця.
--with-incompatible-bdb Якщо ви будуєте гаманець, дозволяє використовувати несумісної версії бібліотеки Berkeley DB.
--with-gui=no Не будувати графічний інтерфейс користувача, що потребує бібліотеку Qt. Це будує тільки сервер та біткоін командного рядка.
Далі виконайте скрипт конфігурації, щоб автоматично визначити всі потрібні бібліотеки, та створити власний скрипт побудови для вашої системи:
$ ./configure
checking build system type... x86_64-unknown-linux-gnu
checking host system type... x86_64-unknown-linux-gnu
checking for a BSD-compatible install... /usr/bin/install -c
checking whether build environment is sane... yes
checking for a thread-safe mkdir -p... /bin/mkdir -p
checking for gawk... gawk
checking whether make sets $(MAKE)... yes
...
[many pages of configuration tests follow]
...
$
Якщо все піде гарно, команда конфігурації завершиться створенням власного скрипта побудови, що дозволить нам побудувати bitcoind. Якщо є відсутні бібліотеки або помилки, команда конфігурації завершиться з помилкою, замість створення скриптів побудови. В разі виникнення помилки це станеться найбільш всього через відсутню або несумісну бібліотеку. Передивіться документацію з побудови, та переконайтесь, що ви встановили відсутні передумови. Потім знову виконайте конфігурацію, та подивіться, чи це вирішило помилку.
rpcuser=bitcoinrpc
rpcpassword=CHANGE_THIS
Example 3-2 shows a resource-constrained node running on a smaller server.
Example 3-2. Sample configuration of a resource-constrained system
alertnotify=myemailscript.sh "Alert: %s"
maxconnections=15
prune=5000
minrelaytxfee=0.0001
maxmempool=200
maxreceivebuffer=2500
maxsendbuffer=500
rpcuser=bitcoinrpc
rpcpassword=CHANGE_THIS
Коли ви відрадегували файл конфігурації, та встановили опції, що найкраще представляють ваші потреби, ви можете протестувати bitcoind в цій конфігурації. Виконайте Bitcoin Core з опцією printtoconsole, щоб виконати його в фоні з виводом в консоль:
$ bitcoind -printtoconsole
Bitcoin version v0.11.20.0
Using OpenSSL version OpenSSL 1.0.2e 3 Dec 2015
Startup time: 2015-01-02 19:56:17
Using data directory /tmp/bitcoin
Using config file /tmp/bitcoin/bitcoin.conf
Using at most 125 connections (275 file descriptors available)
Using 2 threads for script verification
scheduler thread start
HTTP: creating work queue of depth 16
No rpcpassword set - using random cookie authentication
Generated RPC authentication cookie /tmp/bitcoin/.cookie
HTTP: starting 4 worker threads
Bound to [::]:8333
Bound to 0.0.0.0:8333
Cache configuration:
* Using 2.0MiB for block index database
* Using 32.5MiB for chain state database
* Using 65.5MiB for in-memory UTXO set
init message: Loading block index...
Opening LevelDB in /tmp/bitcoin/blocks/index
Opened LevelDB successfully
[... more startup messages ...]
Ви можете натиснути Ctrl-C для переривання процесу, коли ви будете задоволені, потрібні налаштування завантажені, та все робить як ви очікували. Щоб виконати Bitcoin Core в фоні як процес, запустіть його з опцією daemon
bitcoind -daemonЩоб відстежувати перебіг та статус вашого вузла біткоін, використовуйте команду bitcoin-cli getinfo:
$ bitcoin-cli getinfo
{
}
"version" : 110200,
"protocolversion" : 70002,
"blocks" : 396328,
"timeoffset" : 0,
"connections" : 15,
"proxy" : "",
"difficulty" : 120033340651.23696899,
"testnet" : false,
"relayfee" : 0.00010000,
"errors" : ""
Це показує, що вузол виконує Bitcoin Core версії 0.11.2, з висотою блокчейна 396328 блоків, та 15 активних мережевих з'єднань.
Коли ви будете задоволені опціями конфігурації, які ви обрали, ви маєте додати біткоін до скриптів запуску в вашій операційній системі, так що він буде постійно виконуватись та рестартувати, коли рестартує операційна система. Ви знайдете декілька скриптів запуску для різних операційних систем в contrib/init серед джерельного коду біткоіна, та файл README.md показують, які операційні системи використовують які скрипти.
Клієнт Bitcoin Core реалізує інтерфейс JSON-RPC, до якого можна отримати доступ через допоміжну програму командного рядка, bitcoin-cli. Командний рядок дозволяє нам інтерактивно експериментувати з можливостями, що також доступні програмно через API. Щоб почати, викличте команду допомоги, щоб побачити список доступних команд біткоін RPC:
$ bitcoin-cli help
addmultisigaddress nrequired ["key",...] ( "account" )
addnode "node" "add|remove|onetry"
backupwallet "destination"
createmultisig nrequired ["key",...]
createrawtransaction [{"txid":"id","vout":n},...] {"address":amount,...}
decoderawtransaction "hexstring"
...
...
verifymessage "bitcoinaddress" "signature" "message"
walletlock
walletpassphrase "passphrase" timeout
walletpassphrasechange "oldpassphrase" "newpassphrase"
Кожна з ціх команд може сприймати декілька параметрів. Щоб отримати додаткову допомогу, детальний опис, та інформацію щодо параметрів, додайте назву команди після help. Наприклад, щоб побачити допомогу щодо команди getblockhash RPC:
$ bitcoin-cli help getblockhash
getblockhash index
Returns hash of block in best-block-chain at index provided.
Arguments:
1. index
(numeric, required) The block index
Result:
"hash"
(string) The block hash
Examples:
> bitcoin-cli getblockhash 1000
> curl --user myusername --data-binary '{"jsonrpc": "1.0", "id":"curltest",
"method": "getblockhash", "params": [1000] }' -H 'content-type: text/plain;'
http://127.0.0.1:8332/
В кінці інформації допомоги ви можете бачити два приклада команд RPC, використовуючи допоміжник bitcoin-cli, або клієнт HTTP curl. Ці приклади демонструють, як ви можете викликати команду. Скопіюйте перший приклад та побачите результат:
$ bitcoin-cli getblockhash 1000
00000000c937983704a73af28acdec37b049d214adbda81d7e2a3dd146f6ed09
Результом є хеш блоку, що описаний більш детально в наступних главах. Але зараз ця команда повинна повертати той самий результат на вашій системі, демонструючи, що ваш вузол Bitcoin Core робить, сприймаючи команди, та має інформацію про блок 1000, що повертається вам. В наступних розділах ми продемонструємо деякі дуже корисні RPC команди, та їх очікувані результати.
Команда біткоін RPC getinfo відображує базову інформацію щодо статусу мережевого вузла біткоін, гаманця та бази даних блокчейну. Використовуйте bitcoin-cli для її виконання:
$ bitcoin-cli getinfo
{
"version" : 110200,
"protocolversion" : 70002,
}
"blocks" : 396367,
"timeoffset" : 0,
"connections" : 15,
"proxy" : "",
"difficulty" : 120033340651.23696899,
"testnet" : false,
"relayfee" : 0.00010000,
"errors" : ""
Отримані дані повертаються в JavaScript Object Notation (JSON), форматі, що може бути просто “спожитий” всіма мовами програмування, але також є читаємий людиною. Крім цього, ми бачимо номери версій програми-клієнта біткоін (110200) та протокола біткоін (70002). Ми бачимо поточну висоту блока, показуючи нам, як багато блоків відомі клієнту (396367). Також ми бачимо різну статистику щодо мережі біткоін, та налаштування, що мають відношення до клієнта.
Це займе деякий час, можливо більше ніж один день, докі клієнт “наздожене” поточну висоту блокчейну, бо йому треба завантажити всі блоки з інших клієнтів біткоіну. Ви можете перевірити прогрес, використовуючи getinfo, щоб побачити число відомих блоків.
Коли Аліса придбала каву в Bob’s Cafe на початку книги, її транзакція була записана в блокчейні з ID транзакції (txid) 0627052b6f28912f2703066a912ea577f2ce4da4caa5a5fbd8a57286c345c2f2. Давайте використаємо API для отримання та дослідження цієї транзакції, передаючи ID транзакції в якості параметра:
$ bitcoin-cli getrawtransaction
0627052b6f28912f2703066a912ea577f2ce4da4caa5a↵
5fbd8a57286c345c2f2
0100000001186f9f998a5aa6f048e51dd8419a14d8a0f1a8a2836dd734d2804fe65fa35779000↵
000008b483045022100884d142d86652a3f47ba4746ec719bbfbd040a570b1deccbb6498c75c4↵
ae24cb02204b9f039ff08df09cbe9f6addac960298cad530a863ea8f53982c09db8f6e3813014↵
10484ecc0d46f1918b30928fa0e4ed99f16a0fb4fde0735e7ade8416ab9fe423cc54123363767↵
89d172787ec3457eee41c04f4938de5cc17b4a10fa336a8d752adfffffffff0260e3160000000↵
0001976a914ab68025513c3dbd2f7b92a94e0581f5d50f654e788acd0ef8000000000001976a9↵
147f9b1a7fb68d60c536c2fd8aeaa53a8f3cc025a888ac00000000
ID транзакції непевне до того, як вона буде підтвердженою. Відсутність
хеша транзакції в блокчейні не означає, що транзакція не оброблена. Це
відоме як “піддатливість транзакції”, оскільки хеші транзакції можуть бути
змінені до підтвердження блоку. Після підтвердження txid є незмінним та
певним.
Команда getrawtransaction повертає серіалізовану транзакцію в шістнадцятеричній нотації. Щоб декодувати її ми використовуємо команду decoderawtransaction, передаючи шістнадцятирічні дані як параметр. Ви можете копіювати дані, повернуті від getrawtransaction, та вставити їх як параметр до decoderawtransaction:
$ bitcoin-cli decoderawtransaction
0100000001186f9f998a5aa6f048e51dd8419a14d8↵
a0f1a8a2836dd734d2804fe65fa35779000000008b483045022100884d142d86652a3f47ba474↵
6ec719bbfbd040a570b1deccbb6498c75c4ae24cb02204b9f039ff08df09cbe9f6addac960298↵
cad530a863ea8f53982c09db8f6e381301410484ecc0d46f1918b30928fa0e4ed99f16a0fb4fd↵
e0735e7ade8416ab9fe423cc5412336376789d172787ec3457eee41c04f4938de5cc17b4a10fa↵
336a8d752adfffffffff0260e31600000000001976a914ab68025513c3dbd2f7b92a94e0581f5↵
d50f654e788acd0ef8000000000001976a9147f9b1a7fb68d60c536c2fd8aeaa53a8f3cc025a8↵
88ac00000000
{
"txid":
"0627052b6f28912f2703066a912ea577f2ce4da4caa5a5fbd8a57286c345c2f2",
"size": 258,
"version": 1,
"locktime": 0,
"vin": [
{
"txid": "7957a35fe64f80d234d76d83a2...8149a41d81de548f0a65a8a999f6f18",
"vout": 0,
"scriptSig": {
"asm":"3045022100884d142d86652a3f47ba4746ec719bbfbd040a570b1decc...",
"hex":"483045022100884d142d86652a3f47ba4746ec719bbfbd040a570b1de..."
},
"sequence": 4294967295
}
],
"vout": [
{
"value": 0.01500000,
"n": 0,
"scriptPubKey": {
"asm": "OP_DUP OP_HASH160 ab68...5f654e7 OP_EQUALVERIFY OP_CHECKSIG",
"hex": "76a914ab68025513c3dbd2f7b92a94e0581f5d50f654e788ac",
"reqSigs": 1,
"type": "pubkeyhash",
"addresses": [
"1GdK9UzpHBzqzX2A9JFP3Di4weBwqgmoQA"
]
}
},
{
"value": 0.08450000,
"n": 1,
"scriptPubKey": {
"asm": "OP_DUP OP_HASH160 7f9b1a...025a8 OP_EQUALVERIFY OP_CHECKSIG",
"hex": "76a9147f9b1a7fb68d60c536c2fd8aeaa53a8f3cc025a888ac",
"reqSigs": 1,
"type": "pubkeyhash",
"addresses": [
"1Cdid9KFAaatwczBwBttQcwXYCpvK8h7FK"
]
}
}
]
}
Команда transaction decode показує всі компоненти транзакції,
включаючи входи та виходи транзакції. В цьому випадку ми бачимо, що
транзакція поповнила нову адресу на 15 мілібіт, використовувала один вхід,
та згенерувала два виходи. Входом до цієї транзакції був вихід від
попередньо підтвердженої транзакції (показаної як vin txid, що
починається з 7957a35fe). Два виходи відповідають 15 мілібітному кредиту
(оплаті) та виходу зі рештою назад до надсилача.
Ми будемо далі вивчати блокчейн через перевірку попередніх транзакцій, посилаючись на їх txid в цій транзакції, використовуючи ті самі команди(getrawtransaction). Перестрибуючи від транзакції до транзакції ми можемо відслідкувати ланцюжок назад, по мірі того, як монети переходили від однієї адреси до іншої.
Дослідження блоку подібне до дослідження транзакцій. Однак, на блоки можна посилатись або по висоті блоку, або по його хешу. З початку давайте знайдемо блок за його висотою. Раніше ми бачили, що транзакція Аліси була вбудована в блок номер 277316. Ми використовуємо команду getblockhash, що приймає висоту блоку як параметр, та повертає хеш для цього блоку:
$ bitcoin-cli getblockhash 277316
0000000000000001b6b9a13b095e96db41c4a928b97ef2d944a9b31b2cc7bdc4
Тепер, коли ми знаємо, в який блок включена транзакція Аліси, ми можемо отримати цей блок. Ми використовуємо команду getblock з хешем блока в якості параметра:
$ bitcoin-cli getblock
0000000000000001b6b9a13b095e96db41c4a928b97ef2d944a9b3↵
1b2cc7bdc4
{
"hash":
"0000000000000001b6b9a13b095e96db41c4a928b97ef2d944a9b31b2cc7bdc4",
"confirmations": 37371,
"size": 218629,
"height": 277316,
"version": 2,
"merkleroot":
"c91c008c26e50763e9f548bb8b2fc323735f73577effbc55502c51eb4cc7cf2e",
"tx": [
"d5ada064c6417ca25c4308bd158c34b77e1c0eca2a73cda16c737e7424afba2f",
"b268b45c59b39d759614757718b9918caf0ba9d97c56f3b91956ff877c503fbe",
"04905ff987ddd4cfe603b03cfb7ca50ee81d89d1f8f5f265c38f763eea4a21fd",
"32467aab5d04f51940075055c2f20bbd1195727c961431bf0aff8443f9710f81",
"561c5216944e21fa29dd12aaa1a45e3397f9c0d888359cb05e1f79fe73da37bd",
[... hundreds of transactions ...]
"78b300b2a1d2d9449b58db7bc71c3884d6e0579617e0da4991b9734cef7ab23a",
"6c87130ec283ab4c2c493b190c20de4b28ff3caf72d16ffa1ce3e96f2069aca9",
"6f423dbc3636ef193fd8898dfdf7621dcade1bbe509e963ffbff91f696d81a62",
"802ba8b2adabc5796a9471f25b02ae6aeee2439c679a5c33c4bbcee97e081196",
"eaaf6a048588d9ad4d1c092539bd571dd8af30635c152a3b0e8b611e67d1a1af",
"e67abc6bd5e2cac169821afc51b207127f42b92a841e976f9b752157879ba8bd",
"d38985a6a1bfd35037cb7776b2dc86797abbb7a06630f5d03df2785d50d5a2ac",
"45ea0a3f6016d2bb90ab92c34a7aac9767671a8a84b9bcce6c019e60197c134b",
"c098445d748ced5f178ef2ff96f2758cbec9eb32cb0fc65db313bcac1d3bc98f"
],
"time": 1388185914,
"mediantime": 1388183675,
"nonce": 924591752,
"bits": "1903a30c",
"difficulty": 1180923195.258026,
"chainwork":
"000000000000000000000000000000000000000000000934695e92aaf53afa1a",
"previousblockhash":
"0000000000000002a7bbd25a417c0374cc55261021e8a9ca74442b01284f0569",
"nextblockhash":
"000000000000000010236c269dd6ed714dd5db39d36b33959079d78dfd431ba7"
}
Блок містить 419 транзакцій та серед них платіж за каву Аліси має номер 64th (0627052b...). Входження висоти каже нам, що це 277316-й блок в блокчейні.
Допоміжник bitcoin-cli є дуже корисним для дослідження Bitcoin Core API та для тестування функцій. Але загальний смисл програмного інтерфейсу застосування є доступ до функцій програмно. В цьому розділі ми продемонструємо доступ до Bitcoin Core з іншої програми.
Bitcoin Core API є інтерфейсом JSON-RPC. JSON означає JavaScript Object
Notation (об'єктна нотація JavaScript), та це є дуже зручним способом
представляти дані, які одночасно гарно читаютсья людиною та програмами.
RPC означає Remote Procedure Call (віддалений виклик процедур), що
означає, що ми виклакаємо процедури (функції), що віддалені від нас (на
вузлі Bitcoin Core) через мережевий протокол. В цьому випадку мережевим
протоколом є HTTP або HTTPS (для зашифрованих з'єднань).
Коли ви використовували команду bitcoin-cli, щоб отримати допомогу про іншу команду, нам показувався приклад використання curl, швидкий клієнт HTTP командного рядка, що констурює один з ціх викликів JSON-RPC:
$ curl --user myusername --data-binary '{"jsonrpc": "1.0",
"id":"curltest", "method": "getinfo", "params": [] }' -H 'content-type: text/plain;'
http://127.0.0.1:8332/
Ця команда показує, що curl надсилає запит HTTP до локального хосту
(127.0.0.1), під'єднуючись до порту біткоін по замовчанню (8332), та
надсилаючизапит jsonrpc для метода getinfo, використовуючи кодування
text/plain. Якщо ви реалізуєте виклик JSON-RPC в вашій власній програмі,
ви можете використовувати базову бібліотеку HTTP для побудови виклику,
подібно до того, що показаний в попередньому прикладі curl.
Однак, існують бібліотеки майже у усіх мовах програмування, що
"огортають" Bitcoin Core API в такий спосіб, що робить виклики значно
простішими. Ми буде використовувати бібліотеку python-bitcoinlib для
спрощення доступу до API. Пам'ятайте, що це потребує мати діючий екземпляр
Bitcoin Core, що буде використовуватись для виконання викликів JSON-RPC.
Скрипт на Python в Прикладі 3-3 робить простий виклик getinfo, та друкує
параметри блоків з даних, що повертаються Bitcoin Core.
Приклад 3-3. Виконання getinfo чеерз Bitcoin Core JSON-RPC API від bitcoin.rpc
import RawProxy
# Створюємо з'єднання до локального вузла Bitcoin Core
p = RawProxy()
# Виконуємо команду getinfo, зберігаємо результат даних в info
info = p.getinfo()
# Отримання елементу 'blocks' з info
print(info['blocks'])
$ python rpc_example.py
394075
Це каже нам, що наш локальний вузол Bitcoin Core має 394075 блоків в блокчейні. Не дуже яскравий результат, але він демонструє базове використання бібліотеки як спрощеного інтерфейсу до Bitcoin Core JSON-RPC API.
Далі давайте використаємо виклики getrawtransaction та decodetransaction для отримання деталей щодо платежу Аліси. В прикладі 3-4 ми отрумуємо транзакцію Аліси та перелічуємо виходи транзакції. Для кожного виходу ми показуємо адресу отримувача, та суму переказу. Нагадуємо, що транзакція Аліси має один вихід як платіж до Bob’s Cafe, та один вихід для отримання решти Алісою.
Приклад 3-4. Отримання транзакції та сканування виходів від bitcoin.rpc
import RawProxy
p = RawProxy()
# ID транзакції Аліси
txid = "0627052b6f28912f2703066a912ea577f2ce4da4caa5a5fbd8a57286c345c2f2"
# З початку отримуємо сиру транзакцію в hex
raw_tx = p.getrawtransaction(txid)
# Декодуємо транзакцію з hex в об'єкт JSON
decoded_tx = p.decoderawtransaction(raw_tx)
# Отримуємо кожний з виходів від транзакції
for output in decoded_tx['vout']:
print(output['scriptPubKey']['addresses'], output['value'])
$ python rpc_transaction.py
([u'1GdK9UzpHBzqzX2A9JFP3Di4weBwqgmoQA'], Decimal('0.01500000'))
([u'1Cdid9KFAaatwczBwBttQcwXYCpvK8h7FK'], Decimal('0.08450000'))
Обоє з попередніх прикладів досить прості. Насправді вам не треба
програма, щоб виконати їх, ви можете лише скористатись допоміжником
bitcoin-cli. Наступний приклад, однак, потребує декількох сотен викликів
RPC, та більш прозоро демонструє використання програмного інтерфейсу. В
Прикладі 3-5, ми з початку отримуємо блок 277316, потім отримуємо кожну з
419 транзакцій в ньому, через посилання на ID кожної транзакції. Далі ми
ітеруємо по кожному з виходів транзакцій, та додаємо їх значення.
Приклад 3-5. Отримання блоку та додавання всіх виходів його транзакцій від bitcoin.rpc
import RawProxy
p = RawProxy()
# Висота блоку, де зберігаєтся транзакція Аліси
blockheight = 277316
# Отримання хешу блоку з висотою 277316
blockhash = p.getblockhash(blockheight)
# Отримання блоку за хешем
block = p.getblock(blockhash)
# Елемент tx містить список ID всіх транзакцій в блоці
transactions = block['tx']
block_value = 0
# Ітеруємо по кожній з транзакцій в блоці за їх ID
for txid in transactions:
tx_value = 0
# Отримуємо ситу транзакцію за ID
raw_tx = p.getrawtransaction(txid)
# Декодуємо транзакцію
decoded_tx = p.decoderawtransaction(raw_tx)
# Ітеруємо по кожному виходу в транзакції
for output in decoded_tx['vout']:
# Додаємо суму кожного виходу
tx_value = tx_value + output['value']
# Додаємо суму цієї тразакції до загалу
block_value = block_value + tx_value
print("Total value in block: ", block_value)
$ python rpc_block.py
('Total value in block: ', Decimal('10322.07722534'))
Код нашого прикладу обчислює залальну вартість, передану в блоці, що вона складає 10322.07722534 BTC (включаючи винагороду 25 BTC та 0.0909 BTC комісійних). Порівняйте це з сумою, що повідомляє дослідник блоків на деякому сайті, виконавши пошук хешу блока, або його висоту. Деякі дослідники блоків повідомляють загальну суму, за виключенням винагороди та за виключенням комісійних. Побачино, чи помітите ви різницю.
Існує багато альтернативних клієнтів, бібліотек, булкітів та навіть
реалізацій повного вузла в екосистемі біткоіну. Вони реалізовані в різних
програмних мовах, та пропонують природні програмні інтерфейси на улюблених
мовах.
Насутпний розділ перераховує деякі з ціх бібліотек, клієнтів та тулкітів,
впорядкованих за мовами програмування.
C/C++
Bitcoin Core
Референсна реалізація біткоін
libbitcoin
Між-платформений тулкіт розробника на C++, вузол та
бібліотека консенсусу
bitcoin explorer Інструмент командного рядка
Libbitcoin
picocoin
Легковажна C клієнтська бібліотека для біткоіна
від Jeff Garzik
JavaScript
bcoin
Модулярна та
маштабована реалізація повного вузла з API
Bitcore
Повний вузол, API, та
бібліотека від Bitpay
BitcoinJS
Чиста бібліотека JavaScript Bitcoin для
node.js та переглядача
Java
bitcoinj
Бібліотека повного
клієнтського вузла на Java
Bits of Proof (BOP) Реалізація біткоін рівня
підприємства на Java
Python
python-bitcoinlib Бібліотека біткоін на
Python, бібліотека консенсусу, та вузол від Peter Todd
pycoin
Бібліотека біткоін на Python
від Richard Kiss
pybitcointools Бібліотека
біткоін на Python від Vitalik Buterin
Ruby bitcoin-client
Бібліотека на Ruby, огортка до JSON-RPC API
Go btcd
Клієнт повного вузла на мові Go
Rust rust-bitcoin
Бібліотека на Rust для
серіалізації, розбору та викликів API
C# NBitcoin Вичерпна бібліотека біткоін для фреймворку .NET
Objective-C CoreBitcoin Тулкіт біткоін для ObjC та
Swift
Існує багато інших бібліотек на багатьох інших мовах програмування, та
багато створюються весь час.
Мабуть ви чули, що біткоін базується на криптографії, що є галуззю математики, що інтенсивно використовується в комп'ютерній безпеці. Криптографія з грецької означає “потаємне письмо”, але наука криптографії опанувала більше ніж тільки утаємнення письмен, що відоме як шифрування. Криптографія також може бути використана для надання знання щодо секрету без викриття секрету (цифрового підпису), або провадження аутентифічності даних (цифровий підпис). Ці типи криптографічних доказів є математичними інструментами, критичними для біткоіна, та екстенсивно використовуються в застосуваннях біткоіну.
Досить іронічним виглядає те, що шифрування не є важливою частиною біткоіну, бо його комунікації та дані транзакцій не зашифровані, та не мають шифруватись для захисту капіталу. В цій главі ми введемо деяку криптографію, що використовується в біткоіні для контролю за власністю над фондами, в формі ключів, адрес та гаманців.
Власність біткоіну встановлюється через цифрові ключі, адреси біткоіну та цифрові сигнатури. Цифрові ключі несправді не зберігаються в мережі, та, замість цього, створюються та зберігаються користувачем в файлі або простій базі даних, що називається гаманцем. Цифрові ключі в гаманці користувача повністю незалежні від протоколу біткоін, та можуть бути згенеровані та підтримувані програмою користувацького гаманця, без посилань на блокчейн або підключення до інтернету. Ключі забезпечують багато з цікавих властивостей біткоін, включаючи децентралізовану довіру та контроль, атестацію власності, а також модель безпеки на базі криптографічних доказів.
Більшість з транзакцій біткоін потребує валідний цифровий підпис, щоб
бути включеним до блокчейну, що може бути згенерований тільки з секретного
ключа. Таким чином, будь-хто з копією ключа має контроль над біткоіном.
Цифрова сигнатура (підпис), яка використовується для витрати накопичень,
також відома як доказ, в термінах криптографії. Дані доказу в транзакції
біткоін перевіряє вірність щодо власності на фонди, що наразі
витрачаються.
Ключі находять парами, що складаються з приватного (секретного) ключа, та публічного ключа. Думайте про публічний ключ подібно до номера разунку, на про приватний ключ подібно до секретного PIN, або секрету на чеку, що надає контроль над рахунком. Ці цифрові ключі дуже рідко видимі до користувачів біткоін. В більшості випадків вони зберігаються в файлі гаманця, та керуються програмою гаманця біткоін.
В розділі платежу транзакції біткоін, публічний ключ представлний своїм цифровим відтиском, що має назву адреси біткоін, що використовується в той самий спосіб, що і ім'я отримувача на чеку (“Сплачено на користь”). В більшості випадків адреса біткоіну генерується на основі, та відповідає публічному ключеві. Однак не всі адреси біткоін представляють адреси біткоін, вони також можуть представляти інших бенефіціарів, таких, як скрипти, як ми побачимо пізніше в цій главі. Таким чином, адреси біткоіну абстрагують отримувача фондів, роблячі визначення транзакції гнучкими, подібно до паперових чеків: єдиний інструмент платежів, що може бути використаний для платежів на персональні рахунки, розрахунків з компаніями, платежів по рахунках та виплати в готівці. Адреса біткоіну є тільки репрезентацією ключів, що побачать користувачі, оскільки ця частина є єдино потрібною, що вони мають поділяти з усім світом.
З початку ми будемо вводити криптографію та пояснимо математику, що використовується в біткоін. Далі ми подивимось на те, як генеруються ключі, як вони зберігаються та обробляються. Ми будемо переглядати різні формати кодування, що використовуються для представлення приватних та публічних ключів, адрес, та адрес скриптів. Нарешті, ми подивимось на просунуте використання ключів та адрес: марні адреси, мульти сигнатуру, скриптові адреси та паперові гаманці.
Криптографія публічних клюічів була вперше введена в 1970х, та є математичною фундацією для комп'ютерної та інформаційної безпеки.
З часу появи криптографії публічних ключів були винайдені декілька відповідних математичних функцій, таких, як генерація простих чисел та множення еліптичної кривої. Ці математичні функції є практично незворотними, що значить, що вони прості для обчислення в одному напрямку, та практично нездійснені для обчислення в зворотньому напрямку. Базуючись на математичних функціях, криптографія дозволяє створення цифрових секретів та непідробних цифрових підписів. Біткоін використовує множення еліптичної кривої як основу для криптографії.
В біткоіні ми використовуємо криптографію публічного ключа для створення пари ключів, що контролюють доступ до біткоіну. Пара ключів складається з приватного ключа, та походячого від нього унікального публічного ключа. Публічний ключ використовується для отримання фондів, та приватний ключ використовуєтсья для підписування транзакцій для витрачення фондів.
Існує математичне відношення між публічним та приватним ключем, що
дозволяє використання приватного ключа для генерації сигнатур до
повідомлень. Ця сигнатура може бути перевірена з приватним ключем, без
викриття приватного ключа.
При витрачанні біткоіну поточний власник представляє публічний ключ та сигнатуру (кожний раз іншу, але що походить від того ж самого публічного ключа) в транзакції, щоб витратити ці біткоіни. Презентуючі ці публічний ключ та сигнатуру, кожний в мережі біткоін може перевірити та прийняти транзакцію як валідну, підтверджуючи що особа, що переводить біткоін, володіє єю на час трансферу. В більшості реалізацій гаманця приватний та публічний ключі зберігаються разом, як пара ключів, в цілях зручності. Однак публічний ключ може бути обчислений від приватного ключа, так що можливе зберігання тільки приватного ключа.
Гаманець біткоін містить колекцію пар ключів, кожна складається в приватного ключа та публічного ключа. Приватний ключ (k) є числом, що зазвичай обирається випадково. Від приватного ключа, ми використовуємо множення еліптичної кривої, однобічну криптографічну функцію, щоб згенерувати публічний ключ (K). Від публічного ключа (K) ми використовуємо однобічну криптографію, хеш функцію, щоб згенерувати біткоін адресу (A). В цьому розділі ми почнемо генерувати приватний ключ, подивимось на математику елептичної кривої, що використовується для перехід до публічного ключа, та, нарешті, генерування біткоін адреси від публічного ключа. Відношення між приватним ключем, публічним ключем, та адресою біткоін, показана на Малюнку 4-1.
Малюнок 4-1. Приватний ключ, публічний ключ, та адреса біткоін
Чому в біткоін використовується асиметрична криптографія? Вона не
використовується для “шифрування” (створення секрету) транзакції. Скоріше,
корисною важливостю асиметричної криптографії є здатність для генерування
цифрових сигнатур (підписів). Ця сигнатура може бути вироблена тільки
деким, хто має знання щодо приватного ключа. Однак будь-хто з доступом до
публічного ключа та відтиском транзкації може використовувати їх для
перевірки підпису. Ця корисна властивість асиметричної криптографії робить
можливим для будь-кого перевіряти кожну сигнатуру кожної транзакції, при
цьому гарантуючи, що тільки власники приватних ключів можуть спродукувати
валідний підпис.
Приватний ключ - це лише число, обране випадково. Власність та контроль над приватним ключем є коренем контролю користувача над всіма фондами, асоційованими з відповідними адресами біткоін. Приватний ключ має залишатись секретним весь час, оскільки викриття його третій стороні еквівалентно наданню їм контролю над біткоінами, що захищені цім ключем. Приватний ключ має також бути зкопійований та захищений від випадкової втрати, оскільки його неможливо відновити, та фонди, які він захищав, також будуть невідворотньо втрачені назавжди, .
Приватний ключ біткоіна є лише числом. Ви можете обрати ваш приватний ключ випадково, використовуючи лише монету, олівець та папір: киньте монету 256 разів, та ви отримаєте двоїчні цифри випадкового приватного ключа, що ви можете використовувати як приватний ключ. Публічний ключ потім може бути згенерований з приватного ключа.
Перший, та найбільш важливий крок в генеруванні ключа, є пошук джерела ентропії, або випадковості. Створення ключа це просто те ж саме що “Оберіть число від 1 до 2256.” Точний метод, що ви використовуєте для отримання цього числа, не має значення, до тих пір, доки він непередбачуваний або повторюваний. Програма біткоіну використовує генератори операційної системи, на якій робить, щоб спродукувати 256 біт ентропії (випадковості). Зазвичай, генератор випадкових чисел операційної системи ініціалізується через людське джерело випадковості, та ось чому вас можуть запросити випадково порухати мишею протягом декількох секунд.
Більш точно кажучи, приватний ключ може бути любим числом між 1 та n -
1, де n є константою (n = 1.158 * 1077, трохи менше ніж 2256),
визначений як порядок еліптичної кривої, що використовується в біткоіні
(дивіться пояснення в “Криптографія еліптичної кривої”). Щоб створити
такий ключ, ми випадково обираємо 256-бітне число, та перевіряємо, чи воно
меньшим, ніж n - 1. В термінах програмування це звичано досягається через
подачу довшого рядка випадкових біт, отриманих від криптографічно
безпечного джерела випадковості, до хеш алгоритму SHA256, який дуже зручно
спродукує 256-бітне число. Якщо результат менший за n - 1, ми маємо
підходящий приватний ключ. Інакше ми просто продовжуємо ще раз з іншим
випадковим числом.
Не пишіть власний код для створення випадкового числа, або не використовуйте "простий" генератор випадкових чисел, що надається вашою мовою програмування. Використовуйте криптографічно безпечний генератор псевдовипадкових чисел (CSPRNG) з зерном від джерела з достатньою ентропією. Вивчайте документацію бібліотеки генерації випадкових чисел, що ви обираєте, щоб переконатись, що вона криптографічно безпечна. Коректна реалізація CSPRNG є критичною для безпеки ключів.
Наступний випадково згенерований приватний ключ (k) показаний в HEX форматі (256 біт показані як 64 шістнадцятирічні цифри, кожна з 4 біт):
1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD
Розмір простору приватних ключів біткоін (2256) є неуявно великим числом. Це близько 1077 в десятичнй системі. Для порівняння, досяжний нам всевіт за розрахунками містить 1080 атомів. Щоб згенерувати новий ключ за допомогою клієнта Bitcoin Core (дивіться Главу 3), використовуйте команду getnewaddress. З причин безпеки, вона показує тільки публічний ключ, але не приватний. Щоб змусити bitcoind показати приватний ключ, використовуйте команду dumpprivkey. Вона покаже приватний ключ в форматі Base58 checksum-encoded, що називаєтся Wallet Import Format (WIF), що ми дослідимо більш детально в “Формати приватних ключів”. Ось приклад генерації та відображення приватного ключа за допомогою ціх двох команд:
$ bitcoin-cli getnewaddress
1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy
$ bitcoin-cli dumpprivkey 1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy
KxFC1jmwwCoACiCAWZ3eXa96mBM6tb3TYzGmf6YwgdGWZgawvrtJ
Команда dumpprivkey відкриває гаманець, та виділяє приватний
ключ, що був згенерований командою getnewaddress. Неможливо для bitcoind
узнати приватний ключ від публічного ключа, якщо вони обоє не зберігаються
в гаманці. Команда dumpprivkey не генерує приватний ключ з
публічного ключа, бо це неможливо. Команда просто отримує приватний ключ,
що вже відомий гаманцеві, та що був згенерований командою getnewaddress.
Також ви можете використовувати інструмент командного рядка Bitcoin Explorer (дивіться Додаток G) для генерації та показу приватних ключів за допомогою команд seed, ec-new, та ec-to-wif:
$ bx seed | bx ec-new | bx ec-to-wif
5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn
Публічні ключі генеруються з приватних ключів з використанням множення еліптичної кривої, що є незворотною дією : K = k * G, де k є приватним ключем, та G є сталою точкою, що називається точкою генератора, та K є результуючим публічним ключем. Зворотня операція, відома як "пошук дискретного логаріфму", обчислення k при відомому K, так само складна, як спробувати всі можливі значення k, тобто як брутальний перебір. Перед демонстрацією того, як згенерувати публічний ключ з приватного, давайте подивимось на криптографію еліптичної кривої трохі більш детально.
Множення еліптичної кривої є різновидом функцій, що в криптографії називають функціями-пастками: їх легко виконати в одному напрямку (множення), та неможливо виконати в зворотньому напрямку (ділення). Власник приватного ключа може просто створити публічний ключ, та потім поширити його усім світом, знаючи, що ніхто не зможе обернути функцію, та обчислити приватний ключ від публічного ключа. Цей математичний трюк стає основою для несхибних та безпечних цифрових сигнатур (підписів), що доводять власність фондів біткоін.
Криптографія еліптичної кривої є типом асиметричної, або криптографії публічного ключа, що базується на проблемі дискретного логарифму, який виразений через додавання та множення точок еліптичної кривої.
Малюнок 4-2 є прикладом еліптичної кривої, подібно до тої, що
використовується в біткоіні.
Малюнок 4-2. An elliptic curve
Bitcoin uses a specific elliptic curve and set of mathematical constants,
as defined in a
standard called secp256k1, established by the National Institute of
Standards and
Technology (NIST). The secp256k1 curve is defined by the following
function, which
produces an elliptic curve:
y2 = x3 + 7 over � p
or
y2 mod p = x3 + 7 mod p
The mod p (modulo prime number p) indicates that this curve is over a
finite field of
prime order p, also written as � p, where p = 2256 – 232 – 29 – 28 – 27 –
26 – 24 – 1, a very
large prime number.
Because this curve is defined over a finite field of prime order instead
of over the real
numbers, it looks like a pattern of dots scattered in two dimensions,
which makes it
difficult to visualize. However, the math is identical to that of an
elliptic curve over
real numbers. As an example, Малюнок 4-3 shows the same elliptic
curve over a much
smaller finite field of prime order 17, showing a pattern of dots on a
grid. The
secp256k1 bitcoin elliptic curve can be thought of as a much more complex
pattern
of dots on a unfathomably large grid.
Малюнок 4-3. Elliptic curve cryptography: visualizing an elliptic
curve over F(p), with p=17
So, for example, the following is a point P with coordinates (x,y) that is
a point on the
secp256k1 curve:
P =
(55066263022277343669578718895168534326250603453777594175500187360389116729240,
32670510020758816978083085130507043184471273380659243275938904335757337482424)
Example 4-1 shows how you can check this yourself using Python:
Example 4-1. Using Python to confirm that this point is on the elliptic
curve
Python 3.4.0 (default, Mar 30 2014, 19:23:13)
[GCC 4.2.1 Compatible Apple LLVM 5.1 (clang-503.0.38)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> p =
115792089237316195423570985008687907853269984665640564039457584007908834671663
>>> x =
55066263022277343669578718895168534326250603453777594175500187360389116729240
>>> y =
32670510020758816978083085130507043184471273380659243275938904335757337482424
>>> (x ** 3 + 7 - y**2) % p
0
In elliptic curve math, there is a point called the “point at infinity,”
which roughly cor‐
responds to the role of zero in addition. On computers, it’s sometimes
represented by
x = y = 0 (which doesn’t satisfy the elliptic curve equation, but it’s an
easy separate
case that can be checked).
There is also a + operator, called “addition,” which has some properties
similar to the
traditional addition of real numbers that gradeschool children learn.
Given two
points P1 and P2 on the elliptic curve, there is a third point P3 = P1 +
P2, also on the
elliptic curve.
Geometrically, this third point P3 is calculated by drawing a line
between P1 and P2.
This line will intersect the elliptic curve in exactly one additional
place. Call this point
P3' = (x, y). Then reflect in the x-axis to get P3 = (x, –y).
There are a couple of special cases that explain the need for the “point
at infinity.”
If P1 and P2 are the same point, the line “between” P1 and P2 should
extend to be the
tangent on the curve at this point P1. This tangent will intersect the
curve in exactly
one new point. You can use techniques from calculus to determine the slope
of the
tangent line. These techniques curiously work, even though we are
restricting our
interest to points on the curve with two integer coordinates!
In some cases (i.e., if P1 and P2 have the same x values but different y
values), the tan‐
gent line will be exactly vertical, in which case P3 = “point at
infinity.”
If P1 is the “point at infinity,” then P1 + P2 = P2. Similarly, if P2 is
the point at infinity,
then P1 + P2 = P1. This shows how the point at infinity plays the role of
zero.
It turns out that + is associative, which means that (A + B) + C = A + (B
+ C). That
means we can write A + B + C without parentheses and without ambiguity.
Now that we have defined addition, we can define multiplication in the
standard way
that extends addition. For a point P on the elliptic curve, if k is a
whole number, then
kP = P + P + P + ... + P (k times). Note that k is sometimes confusingly
called an
“exponent” in this case.
Starting with a private key in the form of a randomly generated number
k, we multi‐
ply it by a predetermined point on the curve called the generator point G
to produce
another point somewhere else on the curve, which is the corresponding
public key K.
The generator point is specified as part of the secp256k1 standard and is
always the
same for all keys in bitcoin:
K = k * G
where k is the private key, G is the generator point, and K is the
resulting public key, a
point on the curve. Because the generator point is always the same for all
bitcoin
users, a private key k multiplied with G will always result in the same
public key K.
The relationship between k and K is fixed, but can only be calculated in
one direction,
from k to K. That’s why a bitcoin address (derived from K) can be shared
with anyone
and does not reveal the user’s private key (k).
A private key can be converted into a public key, but a public key
cannot be converted back into a private key because the math only
works one way.
Implementing the elliptic curve multiplication, we take the private key
k generated
previously and multiply it with the generator point G to find the public
key K:
K = 1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD * G
Public key K is defined as a point K = (x,y):
K = (x, y)
where,
x = F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
y = 07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB
To visualize multiplication of a point with an integer, we will use the
simpler elliptic
curve over real numbers—remember, the math is the same. Our goal is to
find the
multiple kG of the generator point G, which is the same as adding G to
itself, k times
in a row. In elliptic curves, adding a point to itself is the equivalent
of drawing a tan‐
gent line on the point and finding where it intersects the curve again,
then reflecting
that point on the x-axis.
Малюнок 4-4 shows the process for deriving G, 2G, 4G, as a
geometric operation on the
curve.
Most bitcoin implementations use the OpenSSL cryptographic
library to do the elliptic curve math. For example, to derive the
public key, the function EC_POINT_mul() is used.
Малюнок 4-4. Elliptic curve cryptography: visualizing the
multiplication of a point G by an
integer k on an elliptic curve
A bitcoin address is a string of digits and characters that can be
shared with anyone
who wants to send you money. Addresses produced from public keys consist
of a
string of numbers and letters, beginning with the digit “1.” Here’s an
example of a bit‐
coin address:
1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy
The bitcoin address is what appears most commonly in a transaction as
the “recipi‐
ent” of the funds. If we compare a bitcoin transaction to a paper check,
the bitcoin
address is the beneficiary, which is what we write on the line after “Pay
to the order
of.” On a paper check, that beneficiary can sometimes be the name of a
bank account
holder, but can also include corporations, institutions, or even cash.
Because paper
checks do not need to specify an account, but rather use an abstract name
as the
recipient of funds, they are very flexible payment instruments. Bitcoin
transactions
use a similar abstraction, the bitcoin address, to make them very
flexible. A bitcoin
address can represent the owner of a private/public key pair, or it can
represent some‐
thing else, such as a payment script, as we will see in
“Pay-to-Script-Hash (P2SH)” on
page 151. For now, let’s examine the simple case, a bitcoin address that
represents,
and is derived from, a public key.
The bitcoin address is derived from the public key through the use of
one-way cryp‐
tographic hashing. A “hashing algorithm” or simply “hash algorithm” is a
one-way
function that produces a fingerprint or “hash” of an arbitrary-sized
input. Crypto‐
graphic hash functions are used extensively in bitcoin: in bitcoin
addresses, in script
addresses, and in the mining Proof-of-Work algorithm. The algorithms used
to make
a bitcoin address from a public key are the Secure Hash Algorithm (SHA)
and the
RACE Integrity Primitives Evaluation Message Digest (RIPEMD), specifically
SHA256 and RIPEMD160.
Starting with the public key K, we compute the SHA256 hash and then
compute the
RIPEMD160 hash of the result, producing a 160-bit (20-byte) number:
A = RIPEMD160 SHA256 K
where K is the public key and A is the resulting bitcoin address.
A bitcoin address is not the same as a public key. Bitcoin addresses
are derived from a public key using a one-way function.
Bitcoin addresses are almost always encoded as “Base58Check” (see “Base58
and
Base58Check Encoding” on page 66), which uses 58 characters (a Base58
number sys‐
tem) and a checksum to help human readability, avoid ambiguity, and
protect against
errors in address transcription and entry. Base58Check is also used in
many other
ways in bitcoin, whenever there is a need for a user to read and correctly
transcribe a
number, such as a bitcoin address, a private key, an encrypted key, or a
script hash. In
the next section we will examine the mechanics of Base58Check encoding and
decoding and the resulting representations. Малюнок 4-5 illustrates
the conversion of a public
key into a bitcoin address.
Малюнок 4-5. Public key to bitcoin address: conversion of a public
key into a bitcoin
address
In order to represent long numbers in a compact way, using fewer
symbols, many
computer systems use mixed-alphanumeric representations with a base (or
radix)
higher than 10. For example, whereas the traditional decimal system uses
the 10
numerals 0 through 9, the hexadecimal system uses 16, with the letters A
through F as
the six additional symbols. A number represented in hexadecimal format is
shorter
than the equivalent decimal representation. Even more compact, Base64
representa‐
tion uses 26 lowercase letters, 26 capital letters, 10 numerals, and 2
more characters such as “+” and “/” to transmit binary data over
text-based media such as email.
Base64 is most commonly used to add binary attachments to email. Base58
is a text-
based binary-encoding format developed for use in bitcoin and used in many
other
cryptocurrencies. It offers a balance between compact representation,
readability, and
error detection and prevention. Base58 is a subset of Base64, using upper-
and lower‐
case letters and numbers, but omitting some characters that are frequently
mistaken
for one another and can appear identical when displayed in certain fonts.
Specifically,
Base58 is Base64 without the 0 (number zero), O (capital o), l (lower L),
I (capital i),
and the symbols “+” and “/”. Or, more simply, it is a set of lowercase and
capital letters
and numbers without the four (0, O, l, I) just mentioned. Example 4-2
shows the full
Base58 alphabet.
Example 4-2. Bitcoin’s Base58 alphabet
123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz
To add extra security against typos or transcription errors, Base58Check
is a Base58
encoding format, frequently used in bitcoin, which has a built-in
error-checking
code. The checksum is an additional four bytes added to the end of the
data that is
being encoded. The checksum is derived from the hash of the encoded data
and can
therefore be used to detect and prevent transcription and typing errors.
When pre‐
sented with Base58Check code, the decoding software will calculate the
checksum of
the data and compare it to the checksum included in the code. If the two
do not
match, an error has been introduced and the Base58Check data is invalid.
This pre‐
vents a mistyped bitcoin address from being accepted by the wallet
software as a valid
destination, an error that would otherwise result in loss of funds.
To convert data (a number) into a Base58Check format, we first add a
prefix to the
data, called the “version byte,” which serves to easily identify the type
of data that is
encoded. For example, in the case of a bitcoin address the prefix is zero
(0x00 in hex),
whereas the prefix used when encoding a private key is 128 (0x80 in hex).
A list of
common version prefixes is shown in Table 4-1.
Next, we compute the “double-SHA” checksum, meaning we apply the SHA256
hash-
algorithm twice on the previous result (prefix and data):
checksum = SHA256(SHA256(prefix+data))
From the resulting 32-byte hash (hash-of-a-hash), we take only the first
four bytes.
These four bytes serve as the error-checking code, or checksum. The
checksum is
concatenated (appended) to the end.
The result is composed of three items: a prefix, the data, and a
checksum. This result
is encoded using the Base58 alphabet described previously. Малюнок
4-6 illustrates the
Base58Check encoding process.
Малюнок 4-6. Base58Check encoding: a Base58, versioned, and
checksummed format for
unambiguously encoding bitcoin data
In bitcoin, most of the data presented to the user is
Base58Check-encoded to make it
compact, easy to read, and easy to detect errors. The version prefix in
Base58Check
encoding is used to create easily distinguishable formats, which when
encoded in
Base58 contain specific characters at the beginning of the
Base58Check-encoded pay‐
load. These characters make it easy for humans to identify the type of
data that is
encoded and how to use it. This is what differentiates, for example, a
Base58Check-
encoded bitcoin address that starts with a 1 from a Base58Check-encoded
private key
WIF that starts with a 5. Some example version prefixes and the resulting
Base58
characters are shown in Table 4-1.
Table 4-1. Base58Check version prefix and encoded result examples
Type Version prefix (hex) Base58 result prefix
Bitcoin Address 0x00 1
Pay-to-Script-Hash Address 0x05 3
Bitcoin Testnet Address 0x6F m or n
Table 4-3. Example: Same key, different formats
Hex 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aedd
WIF 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn
WIF-compressed KxFC1jmwwCoACiCAWZ3eXa96mBM6tb3TYzGmf6YwgdGWZgawvrtJ
All of these representations are different ways of showing the same
number, the same
private key. They look different, but any one format can easily be
converted to any
other format. Note that the “raw binary” is not shown in Table 4-3 as any
encoding
for display here would, by definition, not be raw binary data.
We use the wif-to-ec command from Bitcoin Explorer (see Appendix G) to
show
that both WIF keys represent the same private key:
$ bx wif-to-ec 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn
1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aedd
$ bx wif-to-ec KxFC1jmwwCoACiCAWZ3eXa96mBM6tb3TYzGmf6YwgdGWZgawvrtJ
1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aedd
The Bitcoin Explorer commands (see Appendix G) make it easy to write
shell scripts
and command-line “pipes” that manipulate bitcoin keys, addresses, and
transactions.
You can use Bitcoin Explorer to decode the Base58Check format on the
command
line.
We use the base58check-decode command to decode the uncompressed key:
$ bx base58check-decode
5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn
wrapper
{
checksum 4286807748
payload 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aedd
version 128
}
The result contains the key as payload, the WIF version prefix 128, and a
checksum.
Notice that the “payload” of the compressed key is appended with the
suffix 01, sig‐
nalling that the derived public key is to be compressed:
$ bx base58check-decode
KxFC1jmwwCoACiCAWZ3eXa96mBM6tb3TYzGmf6YwgdGWZgawvrtJ
wrapper
{
checksum 2339607926
payload 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aedd01
version 128
}
Малюнок 4-7. Public key compression
Here’s the same public key generated previously, shown as a compressed
public key
stored in 264 bits (66 hex digits) with the prefix 03 indicating the y
coordinate is odd:
K = 03F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
This compressed public key corresponds to the same private key, meaning it
is gener‐
ated from the same private key. However, it looks different from the
uncompressed
public key. More importantly, if we convert this compressed public key to
a bitcoin
address using the double-hash function (RIPEMD160(SHA256(K))) it will
produce a
different bitcoin address. This can be confusing, because it means that a
single private
key can produce a public key expressed in two different formats
(compressed and
uncompressed) that produce two different bitcoin addresses. However, the
private
key is identical for both bitcoin addresses.
Compressed public keys are gradually becoming the default across bitcoin
clients,
which is having a significant impact on reducing the size of transactions
and there‐
fore the blockchain. However, not all clients support compressed public
keys yet.
Example 4-5. Key and address generation and formatting with the
pybitcointools library
import bitcoin
# Generate a random private key
valid_private_key = False
while not valid_private_key:
private_key = bitcoin.random_key()
decoded_private_key = bitcoin.decode_privkey(private_key, 'hex')
valid_private_key = 0 < decoded_private_key < bitcoin.N
print "Private Key (hex) is: ", private_key
print "Private Key (decimal) is: ", decoded_private_key
# Convert private key to WIF format
wif_encoded_private_key = bitcoin.encode_privkey(decoded_private_key,
'wif')
print "Private Key (WIF) is: ", wif_encoded_private_key
# Add suffix "01" to indicate a compressed private key
compressed_private_key = private_key + '01'
print "Private Key Compressed (hex) is: ", compressed_private_key
# Generate a WIF format from the compressed private key (WIF-compressed)
wif_compressed_private_key = bitcoin.encode_privkey(
bitcoin.decode_privkey(compressed_private_key, 'hex'), 'wif')
print "Private Key (WIF-Compressed) is: ", wif_compressed_private_key
# Multiply the EC generator point G with the private key to get a public
key point
public_key = bitcoin.fast_multiply(bitcoin.G, decoded_private_key)
print "Public Key (x,y) coordinates is:", public_key
# Encode as hex, prefix 04
hex_encoded_public_key = bitcoin.encode_pubkey(public_key,'hex')
print "Public Key (hex) is:", hex_encoded_public_key
# Compress public key, adjust prefix depending on whether y is even or odd
(public_key_x, public_key_y) = public_key
if (public_key_y % 2) == 0:
compressed_prefix = '02'
else:
compressed_prefix = '03'
hex_compressed_public_key = compressed_prefix +
bitcoin.encode(public_key_x, 16)
print "Compressed Public Key (hex) is:", hex_compressed_public_key
# Generate bitcoin address from public key
print "Bitcoin Address (b58check) is:",
bitcoin.pubkey_to_address(public_key)
# Generate compressed bitcoin address from compressed public key
print "Compressed Bitcoin Address (b58check) is:", \
bitcoin.pubkey_to_address(hex_compressed_public_key)
Example 4-6 shows the output from running this code.
Example 4-6. Running key-to-address-ecc-example.py
$ python key-to-address-ecc-example.py
Private Key (hex) is:
3aba4162c7251c891207b747840551a71939b0de081f85c4e44cf7c13e41daa6
Private Key (decimal) is:
26563230048437957592232553826663696440606756685920117476832299673293013768870
Private Key (WIF) is:
5JG9hT3beGTJuUAmCQEmNaxAuMacCTfXuw1R3FCXig23RQHMr4K
Private Key Compressed (hex) is:
3aba4162c7251c891207b747840551a71939b0de081f85c4e44cf7c13e41daa601
Private Key (WIF-Compressed) is:
KyBsPXxTuVD82av65KZkrGrWi5qLMah5SdNq6uftawDbgKa2wv6S
Public Key (x,y) coordinates is:
(41637322786646325214887832269588396900663353932545912953362782457239403430124L,
16388935128781238405526710466724741593761085120864331449066658622400339362166L)
Public Key (hex) is:
045c0de3b9c8ab18dd04e3511243ec2952002dbfadc864b9628910169d9b9b00ec↵
243bcefdd4347074d44bd7356d6a53c495737dd96295e2a9374bf5f02ebfc176
Compressed Public Key (hex) is:
025c0de3b9c8ab18dd04e3511243ec2952002dbfadc864b9628910169d9b9b00ec
Bitcoin Address (b58check) is:
1thMirt546nngXqyPEz532S8fLwbozud8
Compressed Bitcoin Address (b58check) is:
14cxpo3MBCYYWCgF74SWTdcmxipnGUsPw3
Example 4-7 is another example, using the Python ECDSA library for the
elliptic
curve math and without using any specialized bitcoin libraries.
Example 4-7. A script demonstrating elliptic curve math used for bitcoin
keys
import ecdsa
import os
from ecdsa.util import string_to_number, number_to_string
# secp256k1, http://www.oid-info.com/get/1.3.132.0.10
_p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2FL
_r = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141L
_b = 0x0000000000000000000000000000000000000000000000000000000000000007L
_a = 0x0000000000000000000000000000000000000000000000000000000000000000L
_Gx = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798L
_Gy = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8L
curve_secp256k1 = ecdsa.ellipticcurve.CurveFp(_p, _a, _b)
generator_secp256k1 = ecdsa.ellipticcurve.Point(curve_secp256k1, _Gx, _Gy,
_r)
oid_secp256k1 = (1, 3, 132, 0, 10)
SECP256k1 = ecdsa.curves.Curve("SECP256k1", curve_secp256k1,
generator_secp256k1,
oid_secp256k1)
ec_order = _r
curve = curve_secp256k1
generator = generator_secp256k1
def random_secret():
convert_to_int = lambda array: int("".join(array).encode("hex"), 16)
# Collect 256 bits of random data from the OS's cryptographically secure
random
generator
byte_array = os.urandom(32)
return convert_to_int(byte_array)
def get_point_pubkey(point):
if point.y() & 1:
key = '03' + '%064x' % point.x()
else:
key = '02' + '%064x' % point.x()
return key.decode('hex')
def get_point_pubkey_uncompressed(point):
key = '04' + \
'%064x' % point.x() + \
'%064x' % point.y()
return key.decode('hex')
# Generate a new private key.
secret = random_secret()
print "Secret: ", secret
# Get the public key point.
point = secret * generator
print "EC point:", point
print "BTC public key:", get_point_pubkey(point).encode("hex")
# Given the point (x, y) we can create the object using:
point1 = ecdsa.ellipticcurve.Point(curve, point.x(), point.y(), ec_order)
assert point1 == point
Example 4-8 shows the output produced by running this script.
Example 4-7 uses os.urandom, which reflects a cryptographically
secure random number generator (CSRNG) provided by the
underlying operating system. In the case of a Unix-like operating
system such as Linux, it draws from /dev/urandom; and in the case
of Windows, it calls CryptGenRandom(). If a suitable randomness
source is not found, NotImplementedError will be raised. While
the random number generator used here is for demonstration pur‐
poses, it is not appropriate for generating production-quality bit‐
coin keys as it is not implemented with sufficient security.
Example 4-8. Installing the Python ECDSA library and running the
ec_math.py script
$ # Install Python PIP package manager
$ sudo apt-get install python-pip
$ # Install the Python ECDSA library
$ sudo pip install ecdsa
$ # Run the script
$ python ec-math.py
Secret:
38090835015954358862481132628887443905906204995912378278060168703580660294000
EC point:
(70048853531867179489857750497606966272382583471322935454624595540007269312627,
105262206478686743191060800263479589329920209527285803935736021686045542353380)
BTC public key:
029ade3effb0a67d5c8609850d797366af428f4a0d5194cb221d807770a1522873
Advanced Keys and Addresses
In the following sections we will look at advanced forms of keys and
addresses, such
as encrypted private keys, script and multisignature addresses, vanity
addresses, and
paper wallets.
Private keys must remain secret. The need for confidentiality of the
private keys is a
truism that is quite difficult to achieve in practice, because it
conflicts with the equally
important security objective of availability. Keeping the private key
private is much
harder when you need to store backups of the private key to avoid losing
it. A private
key stored in a wallet that is encrypted by a password might be secure,
but that wallet
needs to be backed up. At times, users need to move keys from one wallet
to another
—to upgrade or replace the wallet software, for example. Private key
backups might
also be stored on paper (see “Paper Wallets” on page 88) or on external
storage media,
such as a USB flash drive. But what if the backup itself is stolen or
lost? These con‐
flicting security goals led to the introduction of a portable and
convenient standard
for encrypting private keys in a way that can be understood by many
different wallets
and bitcoin clients, standardized by BIP-38 (see Appendix C).
BIP-38 proposes a common standard for encrypting private keys with a
passphrase
and encoding them with Base58Check so that they can be stored securely on
backup
media, transported securely between wallets, or kept in any other
conditions where
the key might be exposed. The standard for encryption uses the Advanced
Encryp‐
tion Standard (AES), a standard established by the NIST and used broadly
in data
encryption implementations for commercial and military applications.
A BIP-38 encryption scheme takes as input a bitcoin private key, usually
encoded in
the WIF, as a Base58Check string with the prefix of “5.” Additionally, the
BIP-38
encryption scheme takes a passphrase—a long password—usually composed of
several words or a complex string of alphanumeric characters. The result
of the BIP-38
encryption scheme is a Base58Check-encoded encrypted private key that
begins with
the prefix 6P. If you see a key that starts with 6P, it is encrypted and
requires a pass‐
phrase in order to convert (decrypt) it back into a WIF-formatted private
key (prefix
5) that can be used in any wallet. Many wallet applications now recognize
BIP-38-
encrypted private keys and will prompt the user for a passphrase to
decrypt and
import the key. Third-party applications, such as the incredibly useful
browser-based
Bit Address (Wallet Details tab), can be used to decrypt BIP-38 keys.
The most common use case for BIP-38 encrypted keys is for paper wallets
that can be
used to back up private keys on a piece of paper. As long as the user
selects a strong
passphrase, a paper wallet with BIP-38 encrypted private keys is
incredibly secure and
a great way to create offline bitcoin storage (also known as “cold
storage”).
Test the encrypted keys in Table 4-5 using bitaddress.org to see how you
can get the
decrypted key by entering the passphrase.
Table 4-5. Example of BIP-38 encrypted private key
Private Key (WIF)
5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn
Passphrase
MyTestPassphrase
Encrypted Key (BIP-38)
6PRTHL6mWa48xSopbU1cKrVjpKbBZxcLRRCdctLJ3z5yxE87MobKoXdTsJ
Pay-to-Script Hash (P2SH) and Multisig Addresses
As we know, traditional bitcoin addresses begin with the number “1” and
are derived
from the public key, which is derived from the private key. Although
anyone can send
bitcoin to a “1” address, that bitcoin can only be spent by presenting the
correspond‐
ing private key signature and public key hash.
Bitcoin addresses that begin with the number “3” are pay-to-script hash
(P2SH)
addresses, sometimes erroneously called multisignature or multisig
addresses. They
designate the beneficiary of a bitcoin transaction as the hash of a
script, instead of the
owner of a public key. The feature was introduced in January 2012 with
BIP-16 (see
Appendix C), and is being widely adopted because it provides the
opportunity to add
functionality to the address itself. Unlike transactions that “send” funds
to traditional
“1” bitcoin addresses, also known as a pay-to-public-key-hash (P2PKH),
funds sent
to “3” addresses require something more than the presentation of one
public key hash
and one private key signature as proof of ownership. The requirements are
designated
at the time the address is created, within the script, and all inputs to
this address will
be encumbered with the same requirements.
A P2SH address is created from a transaction script, which defines who can
spend a
transaction output (for more details, see “Pay-to-Script-Hash (P2SH)” on
page 151).
Encoding a P2SH address involves using the same double-hash function as
used dur‐
ing creation of a bitcoin address, only applied on the script instead of
the public key:
script hash = RIPEMD160(SHA256(script))
The resulting “script hash” is encoded with Base58Check with a version
prefix of 5,
which results in an encoded address starting with a 3. An example of a
P2SH address
is 3F6i6kwkevjR7AsAd4te2YB2zZyASEm1HM, which can be derived using the
Bitcoin
Explorer commands script-encode, sha256, ripemd160, and base58check-encode
(see Appendix G) as follows:
$ echo dup hash160 [ 89abcdefabbaabbaabbaabbaabbaabbaabbaabba ]
equalverify
checksig > script
$ bx script-encode < script | bx sha256 | bx ripemd160 | bx
base58check-encode
--version 5
3F6i6kwkevjR7AsAd4te2YB2zZyASEm1HM
P2SH is not necessarily the same as a multisignature standard
transaction. A P2SH address most often represents a multi-
signature script, but it might also represent a script encoding other
types of transactions.
Currently, the most common implementation of the P2SH function is the
multi-
signature address script. As the name implies, the underlying script
requires more
than one signature to prove ownership and therefore spend funds. The
bitcoin multi-
signature feature is designed to require M signatures (also known as the
“threshold”)
from a total of N keys, known as an M-of-N multisig, where M is equal to
or less than
N. For example, Bob the coffee shop owner from Chapter 1 could use a
multisigna‐
ture address requiring 1-of-2 signatures from a key belonging to him and a
key
belonging to his spouse, ensuring either of them could sign to spend a
transaction
output locked to this address. This would be similar to a “joint account”
as imple‐
mented in traditional banking where either spouse can spend with a single
signature.
Or Gopesh, the web designer paid by Bob to create a website, might have a
2-of-3
multisignature address for his business that ensures that no funds can be
spent unless
at least two of the business partners sign a transaction.
We will explore how to create transactions that spend funds from P2SH (and
multi-
signature) addresses in Chapter 6.
Vanity addresses are valid bitcoin addresses that contain human-readable
messages. For example, 1LoveBPzzD72PUXLzCkYAtGFYmK5vYNR33 is a valid
address that contains the letters forming the word “Love” as the first
four Base-58 letters. Vanity addresses require generating and testing
billions of candidate private keys, until a bitcoin address with the
desired pattern is found. Although there are some optimizations in the
vanity generation algorithm, the process essentially involves picking a
private key at random, deriving the public key, deriving the bitcoin
address, and checking to see
if it matches the desired vanity pattern, repeating billions of times
until a match is found.
Once a vanity address matching the desired pattern is found, the private
key from which it was derived can be used by the owner to spend bitcoin in
exactly the same way as any other address. Vanity addresses are no less or
more secure than any other
address. They depend on the same Elliptic Curve Cryptography (ECC) and SHA
as any other address. You can no more easily find the private key of an
address starting with a vanity pattern than you can any other address.
In Chapter 1, we introduced Eugenia, a children’s charity director
operating in the Philippines. Let’s say that Eugenia is organizing a
bitcoin fundraising drive and wants to use a vanity bitcoin address to
publicize the fundraising. Eugenia will create a vanity address that
starts with “1Kids” to promote the children’s charity fundraiser. Let’s
see how this vanity address will be created and what it means for the
security of Eugenia’s charity.
It’s important to realize that a bitcoin address is simply a number
represented by sym‐
bols in the Base58 alphabet. The search for a pattern like “1Kids” can be
seen as
searching for an address in the range from
1Kids11111111111111111111111111111
to 1Kidszzzzzzzzzzzzzzzzzzzzzzzzzzzzz. There are approximately 5829
(approxi‐
mately 1.4 * 1051) addresses in that range, all starting with “1Kids.”
Table 4-6 shows
the range of addresses that have the prefix 1Kids.
Table 4-6. The range of vanity addresses starting with “1Kids”
From 1Kids11111111111111111111111111111
1Kids11111111111111111111111111112
1Kids11111111111111111111111111113
...
To
1Kidszzzzzzzzzzzzzzzzzzzzzzzzzzzzz
Let’s look at the pattern “1Kids” as a number and see how frequently we
might find this pattern in a bitcoin address (see Table 4-7). An average
desktop computer PC, without any specialized hardware, can search
approximately 100,000 keys per second.
Table 4-7. The frequency of a vanity pattern (1KidsCharity) and average
search time on a
desktop PC
Length Pattern Frequency Average search time
1 1K 1 на 58 keys < 1 milliseconds
2 1Ki 1 на 3,364 50 milliseconds
3 1Kid 1 на 195,000 < 2 seconds
4 1Kids 1 на 11 million 1 minute
5 1KidsC 1 на 656 million 1 hour
6 1KidsCh 1 на 38 billion 2 days
7 1KidsCha 1 на 2.2 trillion 3–4 months
8 1KidsChar 1 на 128 trillion 13–18 years
9 1KidsChari 1 на 7 quadrillion 800 years
10 1KidsCharit 1 на 400 quadrillion 46,000 years
11 1KidsCharity 1 на 23 quintillion 2.5 million years
As you can see, Eugenia won’t be creating the vanity address “1KidsCharity” anytime soon, even if she had access to several thousand computers. Each additional character increases the difficulty by a factor of 58. Patterns with more than seven characters are usually found by specialized hardware, such as custom-built desktops with multiple GPUs. These are often repurposed bitcoin mining “rigs” that are no longer profitable for bitcoin mining but can be used to find vanity addresses. Vanity searches on GPU systems are many orders of magnitude faster than on a general-purpose CPU.
Another way to find a vanity address is to outsource the work to a pool
of vanity min‐ ers, such as the pool at Vanity Pool. A pool is a service
that allows those with GPU hardware to earn bitcoin searching for vanity
addresses for others. For a small pay‐
ment (0.01 bitcoin or approximately $5 at the time of this writing),
Eugenia can outsource the search for a seven-character pattern vanity
address and get results in a few hours instead of having to run a CPU
search for months.
Generating a vanity address is a brute-force exercise: try a random key, check the resulting address to see if it matches the desired pattern, repeat until successful.
Example 4-9 shows an example of a “vanity miner,” a program designed to
find vanity addresses, written in C++. The example uses the libbitcoin
library, which we introduced in “Alternative Clients, Libraries, and
Toolkits” on page 51.
Example 4-9. Vanity address miner
#include <random>
#include <bitcoin/bitcoin.hpp>
// The string we are searching for
const std::string search = "1kid";
// Generate a random secret key. A random 32 bytes.
bc::ec_secret random_secret(std::default_random_engine& engine);
// Extract the Bitcoin address from an EC secret.
std::string bitcoin_address(const bc::ec_secret& secret);
// Case insensitive comparison with the search string.
bool match_found(const std::string& address);
int main()
{
// random_device on Linux uses "/dev/urandom"
// CAUTION: Depending on implementation this RNG may not be secure enough!
// Do not use vanity keys generated by this example in production
std::random_device random;
std::default_random_engine engine(random());
}
// Loop continuously...
while (true)
{
// Generate a random secret.
bc::ec_secret secret = random_secret(engine);
// Get the address.
std::string address = bitcoin_address(secret);
// Does it match our search string? (1kid)
if (match_found(address))
{
// Success!
std::cout << "Found vanity address! " << address << std::endl;
std::cout << "Secret: " << bc::encode_base16(secret) << std::endl;
return 0;
}
}
// Should never reach here!
return 0;
bc::ec_secret random_secret(std::default_random_engine& engine)
{
// Create new secret...
bc::ec_secret secret;
// Iterate through every byte setting a random value...
for (uint8_t& byte: secret)
byte = engine() % std::numeric_limits<uint8_t>::max();
// Return result.
return secret;
}
std::string bitcoin_address(const bc::ec_secret& secret)
{
// Convert secret to payment address
bc::wallet::ec_private private_key(secret);
bc::wallet::payment_address payaddr(private_key);
}
// Return encoded form.
return payaddr.encoded();
bool match_found(const std::string& address)
{
auto addr_it = address.begin();
// Loop through the search string comparing it to the lower case
// character of the supplied address.
for (auto it = search.begin(); it != search.end(); ++it, ++addr_it)
if (*it != std::tolower(*addr_it))
return false;
// Reached end of search string, so address matches.
return true;
}
Example 4-10 uses std::random_device. Depending on the implementation it
may reflect a CSRNG provided by the underlying
operating system. In the case of a Unix-like operating system such as
Linux, it draws from /dev/urandom. The random number generator used here
is for demonstration purposes, and it is not appropriate for generating
production-quality bitcoin keys as it is not implemented with sufficient
security.
The example code must be compiled using a C++ compiler and linked
against the libbitcoin library (which must be first installed on that
system). To run the example, run the vanity-miner executable with no
parameters (see Example 4-10) and it will
attempt to find a vanity address starting with “1kid.”
Example 4-10. Compiling and running the vanity-miner example
$ # Compile the code with g++
$ g++ -o vanity-miner vanity-miner.cpp $(pkg-config --cflags --libs libbitcoin)
$ # Run the example
$ ./vanity-miner
Found vanity address! 1KiDzkG4MxmovZryZRj8tK81oQRhbZ46YT
Secret: 57cc268a05f83a23ac9d930bc8565bac4e277055f4794cbd1a39e5e71c038f3f
$ # Run it again for a different result
$ ./vanity-miner
Found vanity address! 1Kidxr3wsmMzzouwXibKfwTYs5Pau8TUFn
Secret: 7f65bbbbe6d8caae74a0c6a0d2d7b5c6663d71b60337299a1a2cf34c04b2a623
# Use "time" to see how long it takes to find a result
$ time ./vanity-miner
Found vanity address! 1KidPWhKgGRQWD5PP5TAnGfDyfWp5yceXM
Secret: 2a802e7a53d8aa237cd059377b616d2bfcfa4b0140bc85fa008f2d3d4b225349
real
user
sys
0m8.868s
0m8.828s
0m0.035s
The example code will take a few seconds to find a match for the
three-character pattern “kid,” as we can see when we use the time Unix
command to measure the execution time. Change the search pattern in the
source code and see how much longer it
takes for four- or five-character patterns!
Vanity addresses can be used to enhance and to defeat security measures;
they are truly a double-edged sword. Used to improve security, a
distinctive address makes it harder for adversaries to substitute their
own address and fool your customers into
paying them instead of you. Unfortunately, vanity addresses also make it
possible for anyone to create an address that resembles any random
address, or even another vanity address, thereby fooling your customers.
Eugenia could advertise a randomly generated address (e.g., 1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy) to which people can send their donations. Or, she could generate a vanity address that starts with 1Kids, to make it more distinctive. In both cases, one of the risks of using a single fixed address (rather than a separate dynamic address per donor) is that a thief might be able to infiltrate your website and replace it with his own address, thereby diverting donations to himself. If you have advertised your donation address in a number of different places, your users may visually inspect the address before making a payment to ensure it is the same one they saw on your website, on your email, and on your flyer. In the case of a random address like 1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy, the average user will perhaps inspect the first few characters “1J7mdg” and be satisfied that the address matches.
Using a vanity address generator, someone with the intent to steal by substituting a similar-looking address can quickly generate addresses that match the first few characters, as shown in Table 4-8.
Table 4-8. Generating vanity addresses to match a random address
Original Random Address
1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy
Vanity (4-character match) 1J7md1QqU4LpctBetHS2ZoyLV5d6dShhEy
Vanity (5-character match) 1J7mdgYqyNd4ya3UEcq31Q7sqRMXw2XZ6n
Vanity (6-character match) 1J7mdg5WxGENmwyJP9xuGhG5KRzu99BBCX
So does a vanity address increase security? If Eugenia generates the
vanity address
1Kids33q44erFfpeXrmDSz7zEqG2FesZEN, users are likely to look at the vanity
pattern
word and a few characters beyond, for example noticing the “1Kids33” part
of the
address. That would force an attacker to generate a vanity address
matching at least
six characters (two more), expending an effort that is 3,364 times (58 ×
58) higher
than the effort Eugenia expended for her 4-character vanity. Essentially,
the effort
Eugenia expends (or pays a vanity pool for) “pushes” the attacker into
having to produce a longer pattern vanity. If Eugenia pays a pool to
generate an 8-character vanity
address, the attacker would be pushed into the realm of 10 characters,
which is infea‐
sible on a personal computer and expensive even with a custom
vanity-mining rig or
vanity pool. What is affordable for Eugenia becomes unaffordable for the
attacker,
especially if the potential reward of fraud is not high enough to cover
the cost of the
vanity address generation.
Паперові гаманці є приватними ключами біткоін, надрукованими на папері. Часто паперові гаманці також включають відповідну адресу біткоін для зручності, але це не потрібно, бо її можна отримати від приватного ключа. Паперові гаманці є дуже ефективним шляхом для створення резервних копій або офлайн сховищ біткоін, також відомих як "холодні сховища". Як механізм резервного копіювання, паперовий гаманець може запровадити безпеку проти втрати ключа через збій комп'ютера, такий, як відмова жорсткого диску, крадіжка, або випадкове видалення. Як механізм "холодного сховища", якщо ключі паперового гаманця згенеровані офлайн, та ніколи не зберігались на комп'ютерній системі, вони значно більше безпечні проти хакерів, считувачів клавіатури, та інших онлайн загроз.
Паперові гаманці ідуть в багатьох формах, розмірах та виглядах, але не дуже базовому рівні є тільки ключем та адресою, що надруковані на папері. Таблиця 4-9 показує найпростішу форму паперового гаманця.
Таблиця 4-9. Найпростіша форма паперового гаманця, роздруковані біткоін адреса та приватний ключ
Public address 1424C2F4bC9JidNjjTUZCbUxv6Sa1Mt62x
Private key (WIF) 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn
Паперові гаманці можуть бути просто згенеровані з використанням інструменту, як клієнтській JavaScript генератор bitaddress.org. Ця сторінка містить весь код, потрібний для генерації ключів та паперових гаманців, навіть якщо ви повністю відключені від інтернету. Щоб використати його, збережіть сторінку HTML на вашому локальному пристрої, або на зовнішньому флеш пристрої USB. Від'єднайтесь від інтернету, та відкрийте файл в переглядачі. Навіть краще, завантажте ваш комп'ютер з використанням обмеженої операційної системи, як Linux OS з лазерного диску. Любі ключі, згенеровані за допомогою цього інструменту в стані офлайн можуть бути надруковані на локальному принтері по кабелю USB (не бездротовому), і так створивши паперові гаманці, чиї ключі існують тільки на папері та ніколи не зберігались на онлайн системі. Покладіть цей папір в незгораючий сейф, та "надішліть" біткоін на їх біткоін адреси, щоб реалізувати простий, але високоефективний спосіб "холодного зберігання". Малюнок 4-8 показує паперовий гаманець, згенерований сайтом bitaddress.org.
Малюнок 4-8. Приклад простого паперового гаманця від bitaddress.org
Недолік системи паперових гаманців полягає в тому, що вони чутливі до крадіжок. Крадій, що має змогу отримати доступ до папіру, в жодному разі може викрасти його, або сфотографувати ключі, та обрати контроль над біткоінами, що заблоковані ціма ключами. Більш складна система зберігання паперових гаманців використовує шифровані приватні ключі BIP-38. Ключі, надруковані на папері, захищені паролем, який власник має запам'ятати. Без пароля зашифровані ключі не мають сенсу. Також вони все ще кращі за захищений паролем гаманець, оскільки ключі ніколи не були онлайн, та мають бути фізично отримані з сейфу, або інакше фізично безпечного сховища. Малюнок 4-9 показує паперовий гаманець з зашифрованим приватним ключем (BIP-38), створений на сайті bitaddress.org.
Малюнок 4-9. Приклад шифрованого паперового гаманця з bitaddress.org.
Ключове слово “test.”
Хоча ви можете покласти фонди в паперовий гаманець декілька разів, ви
можете списати фонди з них тільки один раз, витративши все. Це так, бо в
процесі розблокування та витрачання фондів деякі гаманці будуть генерувати
адресу решти, якщо ви витратите меньше, ніж ціла сума. Додатково, якщо
комп'ютер, що ви використовуєте для підпису транзакцій, буде зломаний, ви
ризикуєте виказати приватний ключ. Витрачаючи цілий баланс з паперового
гаманця тільки один раз, ви зменшуєте ризик компрометації. Якщо вам треба
тільки невелика сума, надішліть решту на новий паперовий гаманець в тій
самій транзакції.
Паперові гаманці надходять в різних виглядах та розмірах, з багатьма різними можливостями. Деякі призначені для того, щоб дути подарованими, та мають сезонні теми, такі як Новий рік або Різдво. Інші розроблені для зберігання в банкових скринях або сейфах, з приватним ключем, прихованим в деякий спосіб, або через непрозорі наліпки, або вкладені та закорковані в непрозору фольгу. Малюнки 4-10 до 4-12 показують різні приклади паперових гаманців, з можливостями безпеки та зберігання.
Малюнок 4-10. Приклад паперового гаманця з bitcoinpaperwallet.com
з приватним ключем на вкладеному флаєрі
Малюнок 4-11. Паперовий гаманець bitcoinpaperwallet.com з
прихованим приватним ключем
Інші варіанти мають додаткові копії ключа та адреси в формі від'єднуваних
частин, подібних на білетні корінці, що дозволяє вам зберігати декілька
копій для захисту проти вогню, повені, та інших природних лих.
Малюнок 4-12. Приклад паперового гаманця з додатковими копіями ключів на додатковому "коренці"
The word “wallet” is used to describe a few different things in bitcoin.
At a high level, a wallet is an application that serves as the primary
user interface. The
wallet controls access to a user’s money, managing keys and addresses,
tracking the
balance, and creating and signing transactions.
More narrowly, from a programmer’s perspective, the word “wallet” refers
to the data
structure used to store and manage a user’s keys.
In this chapter we will look at the second meaning, where wallets are
containers for
private keys, usually implemented as structured files or simple databases.
In this section we summarize the various technologies used to construct
user-
friendly, secure, and flexible bitcoin wallets.
A common misconception about bitcoin is that bitcoin wallets contain
bitcoin. In
fact, the wallet contains only keys. The “coins” are recorded in the
blockchain on the
bitcoin network. Users control the coins on the network by signing
transactions with
the keys in their wallets. In a sense, a bitcoin wallet is a keychain.
Bitcoin wallets contain keys, not coins. Each user has a wallet con‐
taining keys. Wallets are really keychains containing pairs of pri‐
vate/public keys (see “Private and Public Keys” on page 57). Users
sign transactions with the keys, thereby proving they own the
transaction outputs (their coins). The coins are stored on the
blockchain in the form of transaction outputs (often noted as vout
or txout).
There are two primary types of wallets, distinguished by whether the
keys they con‐
tain are related to each other or not.
The first type is a nondeterministic wallet, where each key is
independently generated
from a random number. The keys are not related to each other. This type of
wallet is
also known as a JBOK wallet from the phrase “Just a Bunch Of Keys.”
The second type of wallet is a deterministic wallet, where all the keys
are derived from
a single master key, known as the seed. All the keys in this type of
wallet are related to
each other and can be generated again if one has the original seed. There
are a num‐
ber of different key derivation methods used in deterministic wallets. The
most com‐
monly used derivation method uses a tree-like structure and is known as a
hierarchical deterministic or HD wallet.
Deterministic wallets are initialized from a seed. To make these easier
to use, seeds
are encoded as English words, also known as mnemonic code words.
The next few sections introduce each of these technologies at a high
level.
In the first bitcoin wallet (now called Bitcoin Core), wallets were
collections of ran‐
domly generated private keys. For example, the original Bitcoin Core
client pregener‐
ates 100 random private keys when first started and generates more keys as
needed,
using each key only once. Such wallets are being replaced with
deterministic wallets
because they are cumbersome to manage, back up, and import. The
disadvantage of
random keys is that if you generate many of them you must keep copies of
all of
them, meaning that the wallet must be backed up frequently. Each key must
be
backed up, or the funds it controls are irrevocably lost if the wallet
becomes inaccessi‐
ble. This conflicts directly with the principle of avoiding address reuse,
by using each
bitcoin address for only one transaction. Address reuse reduces privacy by
associating
multiple transactions and addresses with each other. A Type-0
nondeterministic wal‐
let is a poor choice of wallet, especially if you want to avoid address
reuse because it
means managing many keys, which creates the need for frequent backups.
Although
the Bitcoin Core client includes a Type-0 wallet, using this wallet is
discouraged by
developers of Bitcoin Core. Малюнок 5-1 shows a nondeterministic
wallet, containing a
loose collection of random keys.
The use of nondeterministic wallets is discouraged for anything
other than simple tests. They are simply too cumbersome to back
up and use. Instead, use an industry-standard–based HD wallet
with a mnemonic seed for backup.
Малюнок 5-1. Type-0 nondeterministic (random) wallet: a collection
of randomly generated
keys
Deterministic, or “seeded,” wallets are wallets that contain private
keys that are all
derived from a common seed, through the use of a one-way hash function.
The seed
is a randomly generated number that is combined with other data, such as
an index
number or “chain code” (see “HD Wallets (BIP-32/BIP-44)” on page 96) to
derive the
private keys. In a deterministic wallet, the seed is sufficient to recover
all the derived
keys, and therefore a single backup at creation time is sufficient. The
seed is also suffi‐
cient for a wallet export or import, allowing for easy migration of all
the user’s keys
between different wallet implementations. Малюнок 5-2 shows a
logical diagram of a
deterministic wallet.
Малюнок 5-2. Type-1 deterministic (seeded) wallet: a deterministic
sequence of keys derived
from a seed
HD wallets are a very powerful mechanism for managing many keys and
addresses.
They are even more useful if they are combined with a standardized way of
creating
seeds from a sequence of English words that are easy to transcribe,
export, and
import across wallets. This is known as a mnemonic and the standard is
defined by
BIP-39. Today, most bitcoin wallets (as well as wallets for other
cryptocurrencies) use
this standard and can import and export seeds for backup and recovery
using intero‐
perable mnemonics.
Let’s look at this from a practical perspective. Which of the following
seeds is easier to
transcribe, record on paper, read without error, export, and import into
another wal‐
let?
0C1E24E5917779D297E14D45F14E1A1A
army van defense carry jealous true
garbage claim echo media make crunch
As bitcoin wallet technology has matured, certain common industry
standards have
emerged that make bitcoin wallets broadly interoperable, easy to use,
secure, and flex‐
ible. These common standards are:
• Mnemonic code words, based on BIP-39
• HD wallets, based on BIP-32
• Multipurpose HD wallet structure, based on BIP-43
• Multicurrency and multiaccount wallets, based on BIP-44
These standards may change or may become obsolete by future developments,
but for
now they form a set of interlocking technologies that have become the de
facto wallet
standard for bitcoin.
The standards have been adopted by a broad range of software and hardware
bitcoin
wallets, making all these wallets interoperable. A user can export a
mnemonic gener‐
ated on one of these wallets and import it in another wallet, recovering
all transac‐
tions, keys, and addresses.
Some example of software wallets supporting these standards include
(listed alpha‐
betically) Breadwallet, Copay, Multibit HD, and Mycelium. Examples of
hardware
wallets supporting these standards include (listed alphabetically)
Keepkey, Ledger,
and Trezor.
The following sections examine each of these technologies in detail.
If you are implementing a bitcoin wallet, it should be built as a HD
wallet, with a seed encoded as mnemonic code for backup, follow‐
ing the BIP-32, BIP-39, BIP-43, and BIP-44 standards, as described
in the following sections.
In “Bitcoin Uses, Users, and Their Stories” on page 5 we introduced
Gabriel, an enter‐
prising young teenager in Rio de Janeiro, who is running a simple web
store that sells
bitcoin-branded t-shirts, coffee mugs, and stickers.
Gabriel uses a Trezor bitcoin hardware wallet (Малюнок 5-4) to
securely manage his bit‐
coin. The Trezor is a simple USB device with two buttons that stores keys
(in the
form of an HD wallet) and signs transactions. Trezor wallets implement all
the indus‐
try standards discussed in this chapter, so Gabriel is not reliant on any
proprietary
technology or single vendor solution.
Малюнок 5-4. A Trezor device: a bitcoin HD wallet in hardware
When Gabriel used the Trezor for the first time, the device generated a
mnemonic
and seed from a built-in hardware random number generator. During this
initializa‐
tion phase, the wallet displayed a numbered sequence of words, one by one,
on the
screen (see Малюнок 5-5).
Малюнок 5-5. Trezor displaying one of the mnemonic words
By writing down this mnemonic, Gabriel created a backup (see Table 5-1)
that can be
used for recovery in the case of loss or damage to the Trezor device. This
mnemonic
can be used for recovery in a new Trezor or in any one of the many
compatible soft‐
ware or hardware wallets. Note that the sequence of words is important, so
mnemonic paper backups have numbered spaces for each word. Gabriel had to
carefully record each word in the numbered space to preserve the correct
sequence.
Table 5-1. Gabriel’s paper backup of the mnemonic
1.
army
7.
garbage
2.
van
8.
claim
3.
defense
9.
echo
4.
carry
10.
media
5.
jealous
11.
make
6.
true
12.
crunch
A 12-word mnemonic is shown in Table 5-1, for simplicity. In fact,
most hardware wallets generate a more secure 24-word mnemonic.
The mnemonic is used in exactly the same way, regardless of
length.
For the first implementation of his web store, Gabriel uses a single
bitcoin address,
generated on his Trezor device. This single address is used by all
customers for all
orders. As we will see, this approach has some drawbacks and can be
improved upon
with an HD wallet.
Wallet Technology Details
Let’s now examine each of the important industry standards that are used
by many
bitcoin wallets in detail.
Mnemonic code words are word sequences that represent (encode) a random
num‐
ber used as a seed to derive a deterministic wallet. The sequence of words
is sufficient
to re-create the seed and from there re-create the wallet and all the
derived keys. A
wallet application that implements deterministic wallets with mnemonic
words will
show the user a sequence of 12 to 24 words when first creating a wallet.
That
sequence of words is the wallet backup and can be used to recover and
re-create all
the keys in the same or any compatible wallet application. Mnemonic words
make it
easier for users to back up wallets because they are easy to read and
correctly tran‐
scribe, as compared to a random sequence of numbers.
Mnemonic words are often confused with “brainwallets.” They are
not the same. The primary difference is that a brainwallet consists
of words chosen by the user, whereas mnemonic words are created
randomly by the wallet and presented to the user. This important
difference makes mnemonic words much more secure, because
humans are very poor sources of randomness.
Mnemonic codes are defined in BIP-39 (see Appendix C). Note that BIP-39
is one
implementation of a mnemonic code standard. There is a different standard,
with a
different set of words, used by the Electrum wallet and predating BIP-39.
BIP-39 was
proposed by the company behind the Trezor hardware wallet and is
incompatible
with Electrum’s implementation. However, BIP-39 has now achieved broad
industry
support across dozens of interoperable implementations and should be
considered
the de facto industry standard.
BIP-39 defines the creation of a mnemonic code and seed, which we
describe here in
nine steps. For clarity, the process is split into two parts: steps 1
through 6 are shown
in “Generating mnemonic words” on page 100 and steps 7 through 9 are shown
in
“From mnemonic to seed” on page 101.
Mnemonic words are generated automatically by the wallet using the
standardized
process defined in BIP-39. The wallet starts from a source of entropy,
adds a check‐
sum, and then maps the entropy to a word list:
1. Create a random sequence (entropy) of 128 to 256 bits.
2. Create a checksum of the random sequence by taking the first (entropy-
length/32) bits of its SHA256 hash.
3. Add the checksum to the end of the random sequence.
4. Divide the sequence into sections of 11 bits.
5. Map each 11-bit value to a word from the predefined dictionary of 2048
words.
6. The mnemonic code is the sequence of words.
Малюнок 5-6 shows how entropy is used to generate mnemonic words.
Малюнок 5-6. Generating entropy and encoding as mnemonic words
Table 5-2 shows the relationship between the size of the entropy data and
the length
of mnemonic codes in words.
Table 5-2. Mnemonic codes: entropy and word length
Entropy (bits) Checksum (bits) Entropy + checksum (bits) Mnemonic length
(words)
128
4
132
12
160
5
165
15
192
6
198
18
224
7
231
21
256
8
264
24
The mnemonic words represent entropy with a length of 128 to 256 bits.
The entropy
is then used to derive a longer (512-bit) seed through the use of the
key-stretching
function PBKDF2. The seed produced is then used to build a deterministic
wallet and
derive its keys.
The key-stretching function takes two parameters: the mnemonic and a salt.
The pur‐
pose of a salt in a key-stretching function is to make it difficult to
build a lookup table
enabling a brute-force attack. In the BIP-39 standard, the salt has
another purpose—it
allows the introduction of a passphrase that serves as an additional
security factor
protecting the seed, as we will describe in more detail in “Optional
passphrase in
BIP-39” on page 104.
The process described in steps 7 through 9 continues from the process
described pre‐
viously in “Generating mnemonic words” on page 100:
7. The first parameter to the PBKDF2 key-stretching function is the
mnemonic pro‐
duced from step 6.
8. The second parameter to the PBKDF2 key-stretching function is a salt.
The salt is
composed of the string constant "mnemonic" concatenated with an optional
user-
supplied passphrase string.
9. PBKDF2 stretches the mnemonic and salt parameters using 2048 rounds of
hash‐
ing with the HMAC-SHA512 algorithm, producing a 512-bit value as its final
output. That 512-bit value is the seed.
Малюнок 5-7 shows how a mnemonic is used to generate a seed.
Малюнок 5-7. From mnemonic to seed
The key-stretching function, with its 2048 rounds of hashing, is a
very effective protection against brute-force attacks against the
mnemonic or the passphrase. It makes it extremely costly (in com‐
putation) to try more than a few thousand passphrase and
mnemonic combinations, while the number of possible derived
seeds is vast (2512).
Tables 5-3, 5-4, and 5-5 show some examples of mnemonic codes and the
seeds they
produce (without any passphrase).
Table 5-3. 128-bit entropy mnemonic code, no passphrase, resulting seed
Entropy input (128 bits)
0c1e24e5917779d297e14d45f14e1a1a
Mnemonic (12 words)
army van defense carry jealous true garbage claim echo media make crunch
Passphrase
(none)
Seed (512 bits)
5b56c417303faa3fcba7e57400e120a0ca83ec5a4fc9ffba757fbe63fbd77a89a1a3be4c67196f57c39
a88b76373733891bfaba16ed27a813ceed498804c0570
Table 5-4. 128-bit entropy mnemonic code, with passphrase, resulting seed
Entropy input (128 bits)
0c1e24e5917779d297e14d45f14e1a1a
Mnemonic (12 words)
army van defense carry jealous true garbage claim echo media make crunch
Passphrase
SuperDuperSecret
Seed (512 bits)
3b5df16df2157104cfdd22830162a5e170c0161653e3afe6c88defeefb0818c793dbb28ab3ab091897d0
715861dc8a18358f80b79d49acf64142ae57037d1d54
Table 5-5. 256-bit entropy mnemonic code, no passphrase, resulting seed
Entropy input (256 bits)
2041546864449caff939d32d574753fe684d3c947c3346713dd8423e74abcf8c
Mnemonic (24 words)
cake apple borrow silk endorse fitness top denial coil riot stay wolf
luggage oxygen faint major edit measure invite love trap field dilemma
oblige
Passphrase
(none)
Seed (512 bits)
3269bce2674acbd188d4f120072b13b088a0ecf87c6e4cae41657a0bb78f5315b33b3a04356e53d062e5
5f1e0deaa082df8d487381379df848a6ad7e98798404
The BIP-39 standard allows the use of an optional passphrase in the
derivation of the
seed. If no passphrase is used, the mnemonic is stretched with a salt
consisting of the
constant string "mnemonic", producing a specific 512-bit seed from any
given
mnemonic. If a passphrase is used, the stretching function produces a
different seed
from that same mnemonic. In fact, given a single mnemonic, every possible
pass‐
phrase leads to a different seed. Essentially, there is no “wrong”
passphrase. All pass‐
phrases are valid and they all lead to different seeds, forming a vast set
of possible
uninitialized wallets. The set of possible wallets is so large (2512) that
there is no prac‐
tical possibility of brute-forcing or accidentally guessing one that is in
use.
There are no “wrong” passphrases in BIP-39. Every passphrase
leads to some wallet, which unless previously used will be empty.
The optional passphrase creates two important features:
• A second factor (something memorized) that makes a mnemonic useless on
its
own, protecting mnemonic backups from compromise by a thief.
• A form of plausible deniability or “duress wallet,” where a chosen
passphrase
leads to a wallet with a small amount of funds used to distract an
attacker from
the “real” wallet that contains the majority of funds.
However, it is important to note that the use of a passphrase also
introduces the risk
of loss:
• If the wallet owner is incapacitated or dead and no one else knows the
pass‐
phrase, the seed is useless and all the funds stored in the wallet are
lost forever.
• Conversely, if the owner backs up the passphrase in the same place as
the seed, it
defeats the purpose of a second factor.
While passphrases are very useful, they should only be used in combination
with a
carefully planned process for backup and recovery, considering the
possibility of sur‐
viving the owner and allowing his or her family to recover the
cryptocurrency estate.
BIP-39 is implemented as a library in many different programming
languages:
python-mnemonic
The reference implementation of the standard by the SatoshiLabs team that
pro‐
posed BIP-39, in Python
bitcoinjs/bip39
An implementation of BIP-39, as part of the popular bitcoinJS framework,
in
JavaScript
libbitcoin/mnemonic
An implementation of BIP-39, as part of the popular Libbitcoin framework,
in
C++
There is also a BIP-39 generator implemented in a standalone webpage,
which is
extremely useful for testing and experimentation. Малюнок 5-8 shows
a standalone web
page that generates mnemonics, seeds, and extended private keys.
Малюнок 5-8. A BIP-39 generator as a standalone web page
The page (https://iancoleman.github.io/bip39/) can be used offline in a
browser, or
accessed online.
HD wallets are created from a single root seed, which is a 128-, 256-,
or 512-bit ran‐
dom number. Most commonly, this seed is generated from a mnemonic as
detailed in
the previous section.
Every key in the HD wallet is deterministically derived from this root
seed, which
makes it possible to re-create the entire HD wallet from that seed in any
compatible
HD wallet. This makes it easy to back up, restore, export, and import HD
wallets con‐
taining thousands or even millions of keys by simply transferring only the
mnemonic
that the root seed is derived from.
The process of creating the master keys and master chain code for an HD
wallet is
shown in Малюнок 5-9.
Малюнок 5-9. Creating master keys and chain code from a root seed
The root seed is input into the HMAC-SHA512 algorithm and the resulting
hash is
used to create a master private key (m) and a master chain code (c).
The master private key (m) then generates a corresponding master public
key (M)
using the normal elliptic curve multiplication process m * G that we saw
in “Public
Keys” on page 60.
The chain code (c) is used to introduce entropy in the function that
creates child keys
from parent keys, as we will see in the next section.
Private child key derivation
HD wallets use a child key derivation (CKD) function to derive child keys
from parent
keys.
The child key derivation functions are based on a one-way hash function
that com‐
bines:
• A parent private or public key (ECDSA uncompressed key)
• A seed called a chain code (256 bits)
• An index number (32 bits)
The chain code is used to introduce deterministic random data to the
process, so that
knowing the index and a child key is not sufficient to derive other child
keys. Know‐
ing a child key does not make it possible to find its siblings, unless you
also have the
chain code. The initial chain code seed (at the root of the tree) is made
from the seed,
while subsequent child chain codes are derived from each parent chain
code.
These three items (parent key, chain code, and index) are combined and
hashed to
generate children keys, as follows.
The parent public key, chain code, and the index number are combined and
hashed
with the HMAC-SHA512 algorithm to produce a 512-bit hash. This 512-bit
hash is
split into two 256-bit halves. The right-half 256 bits of the hash output
become the
chain code for the child. The left-half 256 bits of the hash are added to
the parent
private key to produce the child private key. In Малюнок 5-10, we
see this illustrated
with the index set to 0 to produce the “zero” (first by index) child of
the parent.
Малюнок 5-10. Extending a parent private key to create a child
private key
Changing the index allows us to extend the parent and create the other
children in
the sequence, e.g., Child 0, Child 1, Child 2, etc. Each parent key can
have 2,147,483,647 (231) children (231 is half of the entire 232 range
available because the other half is reserved for a special type of
derivation we will talk about later in this
chapter).
Repeating the process one level down the tree, each child can in turn
become a parent
and create its own children, in an infinite number of generations.
Child private keys are indistinguishable from nondeterministic (random)
keys.
Because the derivation function is a one-way function, the child key
cannot be used
to find the parent key. The child key also cannot be used to find any
siblings. If you
have the nth child, you cannot find its siblings, such as the n–1 child or
the n+1 child,
or any other children that are part of the sequence. Only the parent key
and chain
code can derive all the children. Without the child chain code, the child
key cannot
be used to derive any grandchildren either. You need both the child
private key and
the child chain code to start a new branch and derive grandchildren.
So what can the child private key be used for on its own? It can be used
to make a
public key and a bitcoin address. Then, it can be used to sign
transactions to spend
anything paid to that address.
A child private key, the corresponding public key, and the bitcoin
address are all indistinguishable from keys and addresses created
randomly. The fact that they are part of a sequence is not visible
outside of the HD wallet function that created them. Once created,
they operate exactly as “normal” keys.
As we saw earlier, the key derivation function can be used to create
children at any
level of the tree, based on the three inputs: a key, a chain code, and the
index of the
desired child. The two essential ingredients are the key and chain code,
and com‐
bined these are called an extended key. The term “extended key” could also
be thought
of as “extensible key” because such a key can be used to derive children.
Extended keys are stored and represented simply as the concatenation of
the 256-bit
key and 256-bit chain code into a 512-bit sequence. There are two types of
extended
keys. An extended private key is the combination of a private key and
chain code and
can be used to derive child private keys (and from them, child public
keys). An exten‐
ded public key is a public key and chain code, which can be used to create
child pub‐
lic keys (public only), as described in “Generating a Public Key” on page
63.
Think of an extended key as the root of a branch in the tree structure of
the HD wal‐
let. With the root of the branch, you can derive the rest of the branch.
The extended private key can create a complete branch, whereas the
extended public key can only create a branch of public keys.
An extended key consists of a private or public key and chain code.
An extended key can create children, generating its own branch in
the tree structure. Sharing an extended key gives access to the
entire branch.
Extended keys are encoded using Base58Check, to easily export and import
between
different BIP-32–compatible wallets. The Base58Check coding for extended
keys uses
a special version number that results in the prefix “xprv” and “xpub” when
encoded
in Base58 characters to make them easily recognizable. Because the
extended key is
512 or 513 bits, it is also much longer than other Base58Check-encoded
strings we
have seen previously.
Here’s an example of an extended private key, encoded in Base58Check:
xprv9tyUQV64JT5qs3RSTJkXCWKMyU-
goQp7F3hA1xzG6ZGu6u6Q9VMNjGr67Lctvy5P8oyaYAL9CAWrUE9i6GoNM-
KUga5biW6Hx4tws2six3b9c
Here’s the corresponding extended public key, encoded in Base58Check:
xpub67xpozcx8pe95XVuZLHXZeG6XWXHpGq6Qv5cmNfi7cS5mtjJ2tgy-
peQbBs2UAR6KECeeMVKZBPLrtJunSDMstweyLXhRgPxdp14sk9tJPW9
As mentioned previously, a very useful characteristic of HD wallets is
the ability to
derive public child keys from public parent keys, without having the
private keys.
This gives us two ways to derive a child public key: either from the child
private key,
or directly from the parent public key.
An extended public key can be used, therefore, to derive all of the
public keys (and
only the public keys) in that branch of the HD wallet structure.
This shortcut can be used to create very secure public key–only
deployments where a
server or application has a copy of an extended public key and no private
keys what‐
soever. That kind of deployment can produce an infinite number of public
keys and
bitcoin addresses, but cannot spend any of the money sent to those
addresses. Mean‐
while, on another, more secure server, the extended private key can derive
all the cor‐
responding private keys to sign transactions and spend the money.
One common application of this solution is to install an extended public
key on a
web server that serves an ecommerce application. The web server can use
the public
key derivation function to create a new bitcoin address for every
transaction (e.g., for
a customer shopping cart). The web server will not have any private keys
that would
However, the little web store became quite successful and attracted many
orders from
the local community. Soon, Gabriel was overwhelmed. With all the orders
paying the
same address, it became difficult to correctly match orders and
transactions, espe‐
cially when multiple orders for the same amount came in close together.
Gabriel’s HD wallet offers a much better solution through the ability to
derive public
child keys without knowing the private keys. Gabriel can load an extended
public key
(xpub) on his website, which can be used to derive a unique address for
every cus‐
tomer order. Gabriel can spend the funds from his Trezor, but the xpub
loaded on the
website can only generate addresses and receive funds. This feature of HD
wallets is a
great security feature. Gabriel’s website does not contain any private
keys and there‐
fore does not need high levels of security.
To export the xpub, Gabriel uses the web-based software in conjunction
with the Tre‐
zor hardware wallet. The Trezor device must be plugged in for the public
keys to be
exported. Note that hardware wallets will never export private keys—those
always
remain on the device. Малюнок 5-12 shows the web interface Gabriel
uses to export the
xpub.
Малюнок 5-12. Exporting an xpub from a Trezor hardware wallet
Gabriel copies the xpub to his web store’s bitcoin shop software. He
uses Mycelium
Gear, which is an open source web-store plugin for a variety of web
hosting and content platforms. Mycelium Gear uses the xpub to generate a
unique address for every
purchase.
The ability to derive a branch of public keys from an xpub is very
useful, but it comes
with a potential risk. Access to an xpub does not give access to child
private keys.
However, because the xpub contains the chain code, if a child private key
is known, or
somehow leaked, it can be used with the chain code to derive all the other
child pri‐
vate keys. A single leaked child private key, together with a parent chain
code, reveals
all the private keys of all the children. Worse, the child private key
together with a
parent chain code can be used to deduce the parent private key.
To counter this risk, HD wallets use an alternative derivation function
called hard‐
ened derivation, which “breaks” the relationship between parent public key
and child
chain code. The hardened derivation function uses the parent private key
to derive
the child chain code, instead of the parent public key. This creates a
“firewall” in the
parent/child sequence, with a chain code that cannot be used to compromise
a parent
or sibling private key. The hardened derivation function looks almost
identical to the
normal child private key derivation, except that the parent private key is
used as input
to the hash function, instead of the parent public key, as shown in the
diagram in
Малюнок 5-13.
Малюнок 5-13. Hardened derivation of a child key; omits the parent
public key
Table 5-6. HD wallet path examples
HD path
Key described
m/0
The first (0) child private key from the master private key (m)
m/0/0
The first grandchild private key of the first child (m/0)
m/0'/0
The first normal grandchild of the first hardened child (m/0')
m/1/0
The first grandchild private key of the second child (m/1)
M/23/17/0/0 The first great-great-grandchild public key of the first
great-grandchild of the 18th grandchild of the 24th
child
The HD wallet tree structure offers tremendous flexibility. Each parent
extended key
can have 4 billion children: 2 billion normal children and 2 billion
hardened children.
Each of those children can have another 4 billion children, and so on. The
tree can be
as deep as you want, with an infinite number of generations. With all that
flexibility,
however, it becomes quite difficult to navigate this infinite tree. It is
especially diffi‐
cult to transfer HD wallets between implementations, because the
possibilities for
internal organization into branches and subbranches are endless.
Two BIPs offer a solution to this complexity by creating some proposed
standards for
the structure of HD wallet trees. BIP-43 proposes the use of the first
hardened child
index as a special identifier that signifies the “purpose” of the tree
structure. Based on
BIP-43, an HD wallet should use only one level-1 branch of the tree, with
the index
number identifying the structure and namespace of the rest of the tree by
defining its
purpose. For example, an HD wallet using only branch m/i'/ is intended to
signify a
specific purpose and that purpose is identified by index number “i.”
Extending that specification, BIP-44 proposes a multiaccount structure
as “purpose”
number 44' under BIP-43. All HD wallets following the BIP-44 structure are
identi‐
fied by the fact that they only used one branch of the tree: m/44'/.
BIP-44 specifies the structure as consisting of five predefined tree
levels:
m / purpose' / coin_type' / account' / change / address_index
The first-level “purpose” is always set to 44'. The second-level
“coin_type” specifies
the type of cryptocurrency coin, allowing for multicurrency HD wallets
where each
currency has its own subtree under the second level. There are three
currencies
defined for now: Bitcoin is m/44'/0', Bitcoin Testnet is m/44'/1', and
Litecoin is
m/44'/2'.
The third level of the tree is “account,” which allows users to
subdivide their wallets
into separate logical subaccounts, for accounting or organizational
purposes. For
example, an HD wallet might contain two bitcoin “accounts”: m/44'/0'/0'
and
m/44'/0'/1'. Each account is the root of its own subtree.
On the fourth level, “change,” an HD wallet has two subtrees, one for
creating receiv‐
ing addresses and one for creating change addresses. Note that whereas the
previous
levels used hardened derivation, this level uses normal derivation. This
is to allow this
level of the tree to export extended public keys for use in a nonsecured
environment.
Usable addresses are derived by the HD wallet as children of the fourth
level, making
the fifth level of the tree the “address_index.” For example, the third
receiving address
for bitcoin payments in the primary account would be M/44'/0'/0'/0/2.
Table 5-7
shows a few more examples.
Table 5-7. BIP-44 HD wallet structure examples
HD path
Key described
M/44'/0'/0'/0/2
The third receiving public key for the primary bitcoin account
M/44'/0'/3'/1/14 The fifteenth change-address public key for the fourth
bitcoin account
m/44'/2'/0'/0/1
The second private key in the Litecoin main account, for signing
transactions
Транзакції є найбільш важливою частиною системи біткоіну. Все інше в біткоіні розроблене, щоб впевнитись, що транзакції можуть бути створені, розповсюджені в мережі, перевірені, та, нарешті, додані до глобального реєстру транзакцій (блокчейну). Транзакції є структурами даних, що кодують трансфер вартості між учасниками системи біткоіна. Кожна транзакція є публічним записом в блокчейні біткоіна, глобальному реєстрі бухгалтерії з подвійною реєстрацією. В цій главі ми будемо досліджувати всі різноманітні форми транзакцій, що вони мають містити, як вони створюються, як вони перевіряються, та як вони стають частиною сталого запису всіх транзакцій. Коли ми використовуємо термін “гаманець” в цій главі, ми посилаємось не тільки базу даних ключів, але також на програмне забезпечення, що конструює транзакції.
В Главі 2 ми подивились на транзакцію Аліси, що викостала її для
придбання кофе в кав'ярні Боба, використовуючи переглядач блоків (Малюнок
6-1). Застосування переглядача блоків показує транзакцію з алісиної
“адреси” на
“адресу” Боба. Це досить спрощений погляд на те, що міститься в
транзакції. Фактично, як ми побачимо в ції главі, більшість показаної
інформації сконструйована переглядачем блоків, та, насправді , не є
частиною транзакції.
Малюнок 6-1. Транзакція Аліси до Боба
За лаштунками сцени справжня транзакція виглядає дуже відмінно від транзакції, що провадиться типовим переглядачем блоків. Фактично, більшість високорівневих конструкцій, що ми бачили в різних застосуваннях користувацького інтерфейсу біткоіну, неасправді не існують в системі біткоіну.
Ми можемо використовувати інтерфейс командного рядка Bitcoin Core
(getrawtransaction та decoder
awtransaction) для отримання “сирої” транзакції Аліси, її декодування, щоб
побачити, що вона містить насправді. Результат виглядає таким чином:
{
"version": 1,
"locktime": 0,
"vin": [
{
"txid":
"7957a35fe64f80d234d76d83a2a8f1a0d8149a41d81de548f0a65a8a999f6f18",
"vout": 0,
"scriptSig" :
"3045022100884d142d86652a3f47ba4746ec719bbfbd040a570b1deccbb6498c75c4ae24cb02204
b9f039ff08df09cbe9f6addac960298cad530a863ea8f53982c09db8f6e3813[ALL]
0484ecc0d46f1918b30928fa0e4ed99f16a0fb4fde0735e7ade8416ab9fe423cc5412336376789d1
72787ec3457eee41c04f4938de5cc17b4a10fa336a8d752adf",
"sequence": 4294967295
}
],
"vout": [
{
"value": 0.01500000,
"scriptPubKey": "OP_DUP OP_HASH160
ab68025513c3dbd2f7b92a94e0581f5d50f654e7 OP_EQUALVERIFY OP_CHECKSIG"
},
{
"value": 0.08450000,
"scriptPubKey": "OP_DUP OP_HASH160
7f9b1a7fb68d60c536c2fd8aeaa53a8f3cc025a8 OP_EQUALVERIFY OP_CHECKSIG",
}
]
}
Ви можете помітити декілька речей щодо транзакції, здебільшого речі, що відсутні! Де тут адреса Аліси? Де адреса Боба? Де вхід 0.1, “надісланий ” Алісою? В біткоіні немає ані монет, ані надсилача або отримувача, немає балансу, ані разунків, та немає і адрес. Всі ці речі конструюються на вищому рівні для вигід користувача, щоб зробити речі простішими для розуміння.
Ви також могли помітити багато дивних та неочікуваних полів та шістнадцятирічних рядків. Не турбуйтесь, в цій главі ми детально пояснимо кожне показане тут поле.
Фундаментальним будівним блоком транзакцій біткоіну є вихід транзакції. Виходи транзакцій є неподільні частки валюти біткоіну, записчані на блокчейні, та визнані як валідні всією мережею. Повні вузли біткоіну відсліджують всі доступні та витратні виходи, відомі як невитрачені виходи транзакцій (unspent transaction outputs, скорочено UTXO). Множина всіх UTXO відома як UTXO-множина, наразі налічує мільйони UTXO. UTXO-множина зростає по мірі того, як створюються нові UTXO, та зменшується по мірі споживання UTXO. Кожна транзакція представляє зміну (перезід стану) в наборі UTXO.
Коли ми кажемо, що гаманець користувача “отримав” біткоін, ми маємо на увазі, що гаманець детектував UTXO, що може бути витрачене за допомогою одного з ключів, які контролюються цім гаманцем. Таким чином біткоіновим “балансом” користувача є сума всіх UTXO, що може витрачати гаманець користувача, та що можуть бути розкидані по сотням транзакцій та сотням блоків. Концепція балансу створюється застосуванням гаманця. Гаманець обчислює баланс користувача, сканучи блокчейн та накопичуючи вартість кожного UTXO, які гаманець може витратити за допомогою ключів, що контролює. Більшість гаманців підтримують базу даних, щоб зберігати швидке посилання на всі UTXO, які вони можуть витратити за допомогою контрольованих ключів.
Вихід транзакції може бути мати довільне (ціле) значення, визначене як кількість сатоші. Так само, як долар може бути поділений до двох десятичних значень в якості центів, біткоіни можуть бути поділені до восьми десятичних позицій, як сатоші. Хоча вихід може мати довільне значення, коли створений, він стає неділимим. Це важлива характеристика виходів, на яку треба зробити наголос: виходи є дискретними та неподільними одиницями вартості, визначені в цілих сатоші. Невитрачений вихід може бути спожитий транзакцією тільки цілим. Якщо UTXO більший, ніж бажана віртість транзакції, він все одне має бути спожитим цілим, та для транзакції має бути згенерована решта. Іншими словами, якщо ви маєте UTXO вартістю 20 біьткоін, та бажаєте сплатити тільки 1 біткоін, ваша транзакція має спожити весь 20-біткоіновий UTXO, та спродукувати два виходи: один сплачує 1 біткоін до вашого бажаного отримувача, та інший платить 19 біткоінів решти на ваш гаманець. Як результат неподільної природи виходів транзакції, більшість біткоін транзакцій будуть генерувати решту. Уявіть покупця, який бажає придбати напій за $1.50, що бере власний гаманець, та намагаєтсья знайти комбінацію з монет та банкнот, щоб скласти суму в $1.50. Покупець обере точну суму, якщо це можливо, тобто долар і дві чверті ($0.25), або комбінацію менших номіналів (наприклад, шість чвертей), або, якщо необхідно, більшу купюру, як $5. Якщо покупець дасть власнику магазину більше грошей, скажімо, $5, він буде очікувати решту $3.50, що надійдуть назад в гаманець, та будуть доступні для подальших транзакцій. Подібно до цього, транзакції біткоін мають бути створені з користувацького UTXO, в тих номіналах, які доступні користувачеві. Користувач не може обрізати UTXO навпіл, як він не може перерізати доларову банкноту навпіл, та використовувати частини як гроші. Користувацьке застосування гаманця типово буде обирати між доступними UTXO користувача для компонування суми, більшої або рівної до бажаної суми транзакції. Як і в реальному житті, застосування біткоін може використовувати різні стратегії, щоб задовільнити вимогам придбання: комбінувати декілька менших одиниць, пошук точної решти, або пошук єдиної одиниці, що більше ніж сума транзакції, та утворення решти. Всі з ціх складних комбінацій витратних UTXO виконуєтья гаманцем користувача автоматично, та невидимо для користувача. Це має значення тільки в випадку, якщо ви програмно конструююте сирі транзакції з UTXO.
Транзакція споживає попередньо записані невитрачені виходи транзакцій, та створює нові виходи транзакцій, що можуть бути спожиті в подальших транзакціях. Таким чином, частки вартості біткоін рухаються далі, від власника до власника, в ланцюгу транзакцій, що споживають та створюють UTXO.
Виключення до ланцюга входів та виходів є особливий тип транзакцій, що називаються коінбейс транзакціями в кожному блоці. Ця транзакція записуєтсья “переможним” майнером, та створює повністю нові біткоіни, якими майнер може розраховуватись в якості винагороди за майнинг. Ця особлива коінбейс транзакція не споживає UTXO; замість цього, це особливий тип входу з назвою “коінбейс”. Саме в цей спосіб створюється біткоін в результаті процесу майнингу, як ми побачимо в Главі 10.
Що виникло першим, входи або виходи, курча або яйце? Кажучи відверто, виходи надходять першими, завдяки коінбейс транзакціям, що генерують новий біткоін, не маючи входів, та створюючи виходи з нічого.
Кожна транзакція біткоін створює виходи, що записуються в реєстрі біткоіна. Майже всі з ціх виходів, за одним виключенням (дивіться “Вихід запису даних (RETURN)”), створюють витратні частини біткоіна, що називаються UTXO, що потім розпізнаються всією мережею, та доступні для власника, щоб споживати в наступній транзакції.
UTXO відсліджуються кожним повним вузлом біткоін, в наборі UTXO. нові транзакції споживають (вирачають) один або більше з ціх виходів з набору UTXO.
Виходи транзакцій складаютья з двох частин:
• Сума біткоін, виражена в сатоші, найменьшій одиниці біткоіна
• Криптографічна загадка, що визначає умови, потрібні для витрачання
виходу
Криптографічна загадка, також відома як блокуючий скрипт, або
підтверджуючий скрипт, або scriptPubKey.
Скриптова мова транзакцій, що використовується в згаданому блокуючому скрипті, обговорюється в деталях в “Скрипти транзакцій та скриптова мова”. Тепер давайте поглянемо на транзакцю Аліси (показану раніше в цій главі), та подивимось, чи ми зможемо ідентифікувати виходи. В кодуванні JSON виходи надходять в масиві (списку) на ім'я vout:
"vout": [
{
"value": 0.01500000,
"scriptPubKey": "OP_DUP OP_HASH160
ab68025513c3dbd2f7b92a94e0581f5d50f654e7
OP_EQUALVERIFY
OP_CHECKSIG"
},
{
"value": 0.08450000,
"scriptPubKey": "OP_DUP OP_HASH160
7f9b1a7fb68d60c536c2fd8aeaa53a8f3cc025a8
OP_EQUALVERIFY OP_CHECKSIG",
}
]
Як ви можете бачити, транзакція містить два виходи. Кожинй вихід визначений через значення та криптографічну загадку. В кодуванні Bitcoin Core, значення надане в біткоінах, але сама транзакція записана як ціле, деноміноване в сатоші. Друга частина кожного виходу є криптографічна загадка, що визначає умови витрачання. Bitcoin Core показує це як scriptPubKey, так показує нам людино-орієнтоване представлення скрипта.
Тема блокування та розблокування UTXO буде обговорюватись пізніше, в розділі “Конструкція скрипта (блокування + розблокування)”. Мова скриптів, що використовується для скрипта в scriptPubKey, обговорюється в “Скрипти транзакцій та мова скриптів”. Але перед тим, як ми заглибимось в ці теми, нам треба зрозуміти загальну структуру входів та виходів транзакцій.
Коли транзакція передаєтся по мережі, або обміюється між застосуваннями,
вона серіалізується. Сериалізація є процесом конвертації внутрішнього
представлення структури даних в формат, що може бути переданий байт за
байтом, що також відоме як потік байтів. Сериалізація найбільш загально
використовується для кодування структур даних, для передачі по мережі або
для зберігання в файлі. Формат сериалізації транзакції показаний в Таблиці
6-1.
Таблиця 6-1. Сериалізація виходу транзакції
Розмір Поле Опис
8 байт (little-endian) Сума Вартість біткоін в сатоші (10-8 біткоіну)
1–9 bytes (VarInt) Розмір блокуючого скрипта в байтах
Зміний Блокуючий скрипт, що визначає умови, потрібні для витрати виходу
Більшість бібліотек та фреймворків біткоіну не зберігають транзакції самі
по собі як потоки байтів, бо знадобиться складний робір кожного разу, коли
треба отримати доступ до одного поля. Для зручності та читаємості
біблиотеки біткоін зберігають транзакції всередині як структури даних
(зазавичай, об'єктно-орієнтованих структурах).
Процес перетворення від представлення байт-потоку транзакцій до внутрішньої структури даних бібліотеки має назву десеариалізації, або розбором транзації. Процес конвертації в зворотньому напрямку до потоку байтів для передачі по мережі , хешування, або зберігання на диску, має назву сериалізації. Більшість бібліотек біткоін мають вбудовані функції для перетворень сериалізації та десеариалізації.
Подивимось, чи ви зможнте вручну декодувати транзакцію Аліси з
серіалізованої щістнадцятиричної форми, винайшовши деякі з елементів, що
ми бачили разніше. Розділ містить два виходи в Прикладі 6-1, щоб допомогти
вам:
Приклад 6-1. Транзакція Аліси, серіалізована та представлена в
шістнадцятирічній нотації
0100000001186f9f998a5aa6f048e51dd8419a14d8a0f1a8a2836dd73
4d2804fe65fa35779000000008b483045022100884d142d86652a3f47
ba4746ec719bbfbd040a570b1deccbb6498c75c4ae24cb02204b9f039
ff08df09cbe9f6addac960298cad530a863ea8f53982c09db8f6e3813
01410484ecc0d46f1918b30928fa0e4ed99f16a0fb4fde0735e7ade84
16ab9fe423cc5412336376789d172787ec3457eee41c04f4938de5cc1
7b4a10fa336a8d752adfffffffff0260e31600000000001976a914ab6
8025513c3dbd2f7b92a94e0581f5d50f654e788acd0ef800000000000
1976a9147f9b1a7fb68d60c536c2fd8aeaa53a8f3cc025a888ac 00000000
Ось деякі підказки:
• Тут два виходи в підкресленому розділі, кожний серіалізований як
показано в Таблиці 6-1.
• Значення 0.015 біткоіннів те саме, що 1,500,000 сатоші. Це 16 e3 60
шістнадцятерічною.
• В серіалізованій транзакції значення 16 e3 60 закодоване в порядку байт
little-endian (найменш значущий байт перший), так що це виглядає 60 e3 16.
• Довжина scriptPubKey є 25 байт, що шістнадцятирічною є 19.
Входи транзакції ідентифікують (через посилання), UTXO, що буде спожите, та провадить доказ власності через посередництво розблокуючого скрипта.
Щоб побудувати транзакцію, гаманець обирає з контрольованих ним UTXO, UTXO з достатньою вартістю, щоб зробити запитаний платіж. Іноді досить одного UTXO, іншого разу потрібно більше одного. Для кожного UTXO, що буде спожите для виконання цього платежу, гаманець створює один вхід, що вказує на UTXO, та відмикає його за допомогою розблокуючого скрипта.
Давайте подивимось на компоненти входу більш детально. Черша частина входу є вказівник на UTXO через посилання на хеш транзакції, та номера послідовності, де UTXO записаний в блокчейні. Друга частина є розблокуючий скрипт, що конструює гаманець, щоб задовільнити умові витрачання, встановленій в UTXO. ЧАстіше за все розблокуючий скрипт є цифровим підписом та публічним ключем, що провадять власність біткоіну. Однак, не всі відмикаючі скрипти містять сигнатури. Третя частина є послідовним номером, що буде обговорене пізніше.
Розглянемо наш приклад в “Транзакції: за лаштунками сцени”. В ходи
транзакції є масивом (списком), що називаються vin:
"vin": [
{
"txid":
"7957a35fe64f80d234d76d83a2a8f1a0d8149a41d81de548f0a65a8a999f6f18",
"vout": 0,
"scriptSig" :
"3045022100884d142d86652a3f47ba4746ec719bbfbd040a570b1deccbb6498c75c4ae24cb02204
b9f039ff08df09cbe9f6addac960298cad530a863ea8f53982c09db8f6e3813[ALL]
0484ecc0d46f1918b30928fa0e4ed99f16a0fb4fde0735e7ade8416ab9fe423cc5412336376789d1
72787ec3457eee41c04f4938de5cc17b4a10fa336a8d752adf",
"sequence": 4294967295
}
]
Як ви бачите, в списку тільки один вхід (оскільки один UTXO містить
досить вартості для платежу). Вхід містить чотири елементи:
• ID транзакції, що посилаєтсья на транзакцію, що містить UTXO, що буде
витрачено
• Інедкс виходу (vout), що ідентифікує, на який UTXO з транзакції іде
посилання (починаючи з нуля)
• scriptSig, що задовільняє умовам, покладеним до UTXO, що розблокує для
витрачання
• Послідовний номер (обговорюється пізніше)
В транзакції Аліси вхід вказує на ID транзакції:
7957a35fe64f80d234d76d83a2a8f1a0d8149a41d81de548f0a65a8a999f6f18
та індекс входу 0 (тобто, це перший UTXO, створений цією транзакцією).
Розблокуючий скрипт побудований гаманцем Аліси, зпершу отримавши посиланий
UTXO, перевіривши блокуючий скрипт, та потім використовуючи його для
побудови потрібного розблокуючого скрипту, що задовільнить йому.
Дивлячись тільки на вхід, ви можете помітити, що ми нічого не знаємо щодо
цього UTXO, окрім посилання на транзакцію, що містить його. Ми не знаємо
його вартість (кількість сатоші), та ми не знаємо блокуючий скрипт, що
встановлює умови для його витрачання. Щоб знайти цю інформацію, ми повинні
отримати посилане UTXO, отримавши підлеглу транзакцію. Зауважте, що
оскільки вартість входу явно не зазначена, нам треба також використовувати
посилане UTXO, щоб обчислити комісійні, що будуть сплачені за транзакцію
(дивіться “Комісійні за транзакцію”). Це не тільки гаманець Аліси, хто
потребує отримати UTXO, посиланий у вході. Коли ця транзакція поширюється
мережею, кожний перевіряючий вузол також буде потребувати отримання UTXO,
на який посилаються як на вхід транзакції, щоб перевірити транзакцію.
Транзакції самі по собі виглядають неповними, бо їм бракує контексту. Вони
посилаються на UTXO у своїх входах, але без отримання ціх UTXO ми не
можемо знати вартість входів, або їх блокуючі умови. Коли пишете програмне
забезпечення біткоін, кожного разу, коли ви декодуєте транзакцію з наміром
її перевірки, або з метою підрахування комісійних, або перевіряючі
розблокуючих скрипт, ваш код зпочатку має отримати посилане UTXO з
блокчейна, щоб побудувати контекст, що мається на увазі, але не присутній
в UTXO посиланнях у входах. Наприклад, щоб обчислити суму, сплачену як
комісійні, вам треба знати суму значень входів та виходів. Але без
отримання UTXO посилань у входах, ви не знаєте їх вартість. Так що на
перший вигляд проста операція, як підрахунок комісійних однієї транзакції,
фактчно включає багато кроків та даних з декількох транзакцій.
Ми можемо використати ту саму послідовність команд за допомогою Bitcoin Core, що ми використовували, коли отримували транзакцію Аліси (getrawtransaction та decoderawtransaction). Таким чином ми можемо отримати посилане UTXO в попередньому вході, та поглянути на нього:
"vout": [
{
"value": 0.10000000,
"scriptPubKey": "OP_DUP OP_HASH160
7f9b1a7fb68d60c536c2fd8aeaa53a8f3cc025a8 OP_EQUALVERIFY OP_CHECKSIG"
}
]
Ми бачимо, що цей UTXO має значення 0.1 BTC, та що він має блокуючий скрипт (PubKey), що містить “OP_DUP OP_HASH160...”.
Щоб повністю зрозуміти транзакцію Аліси, нам треба отримати попередні транзакції, на які є повилання у вході. Функція, що отримує попередні транзакції та невитрачені транзакції, є дуже загальною, та існує для кожної бібліотеки та API біткоіну.
Коли транзакції суриалізуються для передачі по мережі, їх входи
кодуються в потік байтів, як показано в Таблиці 6-2.
Таблиця 6-2. Сериалізація входів транзакцій
Розмір Поле Опис
32 байт Хеш транзакції Вказівник на транзакцію, що
містить UTXO до витрати
4 байти Індекс виходу Номер індексу UTXO, що буде витрачено; перший
індекс 0
1–9 байт (VarInt) Розмір розблокуючого скрипта в байтах
Variable Розблокуючий скрипт, що задовільняє умовам блокуючого скрипта
UTXO
4 байти Послідовний номер, використовується для часу блокування, або
відключене (0xFFFFFFFF)
Так само, як для виходів. давайте поглянемо, чи ми можемо знайти входи з
транзакції Аліси в серіалізованому форматі. Зпершу, декодуємо формат
входів:
"vin": [
{
"txid": "7957a35fe64f80d234d76d83a2a8f1a0d8149a41d81de548f0a65a8a999f6f18",
"vout": 0,
"scriptSig" :
"3045022100884d142d86652a3f47ba4746ec719bbfbd040a570b1deccbb6498c75c4ae24cb02204
b9f039ff08df09cbe9f6addac960298cad530a863ea8f53982c09db8f6e3813[ALL]
0484ecc0d46f1918b30928fa0e4ed99f16a0fb4fde0735e7ade8416ab9fe423cc5412336376789d1
72787ec3457eee41c04f4938de5cc17b4a10fa336a8d752adf",
"sequence": 4294967295
}
],
Тепер давайте подивимось, чи ми можемо ідентифікувати ці поля в серіалізованому шістнадцятирічному кодування в Прикладі 6-2:
Example 6-2. Alice’s transaction, serialized and presented in hexadecimal notation
0100000001186f9f998a5aa6f048e51dd8419a14d8a0f1a8a2836dd73 4d2804fe65fa35779000000008b483045022100884d142d86652a3f47 ba4746ec719bbfbd040a570b1deccbb6498c75c4ae24cb02204b9f039 ff08df09cbe9f6addac960298cad530a863ea8f53982c09db8f6e3813 01410484ecc0d46f1918b30928fa0e4ed99f16a0fb4fde0735e7ade84 16ab9fe423cc5412336376789d172787ec3457eee41c04f4938de5cc1 7b4a10fa336a8d752adfffffffff0260e31600000000001976a914ab6 8025513c3dbd2f7b92a94e0581f5d50f654e788acd0ef800000000000 1976a9147f9b1a7fb68d60c536c2fd8aeaa53a8f3cc025a888ac00000 000
Hints:
• The transaction ID is serialized in reversed byte order, so it starts with (hex) 18 and ends with 79 • The output index is a 4-byte group of zeros, easy to identify • The length of the scriptSig is 139 bytes, or 8b in hex • The sequence number is set to FFFFFFFF, again easy to identify
Most transactions include transaction fees, which compensate the bitcoin miners for securing the network. Fees also serve as a security mechanism themselves, by making it economically infeasible for attackers to flood the network with transactions. Min‐ 126 | Chapter 6: Transactions ing and the fees and rewards collected by miners are discussed in more detail in Chapter 10.
This section examines how transaction fees are included in a typical
transaction.
Most wallets calculate and include transaction fees automatically.
However, if you are
constructing transactions programmatically, or using a command-line
interface, you
must manually account for and include these fees.
Transaction fees serve as an incentive to include (mine) a transaction
into the next
block and also as a disincentive against abuse of the system by imposing a
small cost
on every transaction. Transaction fees are collected by the miner who
mines the block
that records the transaction on the blockchain.
Transaction fees are calculated based on the size of the transaction in
kilobytes, not
the value of the transaction in bitcoin. Overall, transaction fees are set
based on mar‐
ket forces within the bitcoin network. Miners prioritize transactions
based on many
different criteria, including fees, and might even process transactions
for free under
certain circumstances. Transaction fees affect the processing priority,
meaning that a
transaction with sufficient fees is likely to be included in the next
block mined,
whereas a transaction with insufficient or no fees might be delayed,
processed on a
best-effort basis after a few blocks, or not processed at all. Transaction
fees are not
mandatory, and transactions without fees might be processed eventually;
however,
including transaction fees encourages priority processing.
Over time, the way transaction fees are calculated and the effect they
have on transac‐
tion prioritization has evolved. At first, transaction fees were fixed and
constant
across the network. Gradually, the fee structure relaxed and may be
influenced by
market forces, based on network capacity and transaction volume. Since at
least the
beginning of 2016, capacity limits in bitcoin have created competition
between trans‐
actions, resulting in higher fees and effectively making free transactions
a thing of the
past. Zero fee or very low fee transactions rarely get mined and sometimes
will not
even be propagated across the network.
In Bitcoin Core, fee relay policies are set by the minrelaytxfee option.
The current
default minrelaytxfee is 0.00001 bitcoin or a hundredth of a millibitcoin
per kilo‐
byte. Therefore, by default, transactions with a fee less than 0.0001
bitcoin are treated
as free and are only relayed if there is space in the mempool; otherwise,
they are
dropped. Bitcoin nodes can override the default fee relay policy by
adjusting the value
of minrelaytxfee.
Any bitcoin service that creates transactions, including wallets,
exchanges, retail
applications, etc., must implement dynamic fees. Dynamic fees can be
implemented
through a third-party fee estimation service or with a built-in fee
estimation algo‐
rithm. If you’re unsure, begin with a third-party service and as you gain
experience
design and implement your own algorithm if you wish to remove the
third-party
dependency.
Fee estimation algorithms calculate the appropriate fee, based on
capacity and the
fees offered by “competing” transactions. These algorithms range from
simplistic
(average or median fee in the last block) to sophisticated (statistical
analysis). They
estimate the necessary fee (in satoshis per byte) that will give a
transaction a high
probability of being selected and included within a certain number of
blocks. Most
services offer users the option of choosing high, medium, or low priority
fees. High
priority means users pay higher fees but the transaction is likely to be
included in the
next block. Medium and low priority means users pay lower transaction fees
but the
transactions may take much longer to confirm.
Many wallet applications use third-party services for fee calculations.
One popular
service is http://bitcoinfees.21.co, which provides an API and a visual
chart showing
the fee in satoshi/byte for different priorities.
Static fees are no longer viable on the bitcoin network. Wallets that
set static fees will produce a poor user experience as transactions
will often get “stuck” and remain unconfirmed. Users who don’t
understand bitcoin transactions and fees are dismayed by “stuck”
transactions because they think they’ve lost their money.
The chart in Малюнок 6-2 shows the real-time estimate of fees in
10 satoshi/byte incre‐
ments and the expected confirmation time (in minutes and number of blocks)
for
transactions with fees in each range. For each fee range (e.g., 61–70
satoshi/byte), two
horizontal bars show the number of unconfirmed transactions (1405) and
total num‐
ber of transactions in the past 24 hours (102,975), with fees in that
range. Based on
the graph, the recommended high-priority fee at this time was 80
satoshi/byte, a fee
likely to result in the transaction being mined in the very next block
(zero block
delay). For perspective, the median transaction size is 226 bytes, so the
recommended
fee for a transaction size would be 18,080 satoshis (0.00018080 BTC).
The fee estimation data can be retrieved via a simple HTTP REST API, at
https://
bitcoinfees.21.co/api/v1/fees/recommended. For example, on the command
line using
the curl Команда:
$ curl https://bitcoinfees.21.co/api/v1/fees/recommended
{"fastestFee":80,"halfHourFee":80,"hourFee":60}
The API returns a JSON object with the current fee estimate for fastest
confirmation
(fastestFee), confirmation within three blocks (halfHourFee) and six
blocks (hour
Fee), in satoshi per byte.
Малюнок 6-2. Fee estimation service bitcoinfees.21.co
The data structure of transactions does not have a field for fees.
Instead, fees are
implied as the difference between the sum of inputs and the sum of
outputs. Any
excess amount that remains after all outputs have been deducted from all
inputs is the
fee that is collected by the miners:
Fees = Sum(Inputs) – Sum(Outputs)
This is a somewhat confusing element of transactions and an important
point to
understand, because if you are constructing your own transactions you must
ensure
you do not inadvertently include a very large fee by underspending the
inputs. That
means that you must account for all inputs, if necessary by creating
change, or you
will end up giving the miners a very big tip!
For example, if you consume a 20-bitcoin UTXO to make a 1-bitcoin payment,
you
must include a 19-bitcoin change output back to your wallet. Otherwise,
the 19-
bitcoin “leftover” will be counted as a transaction fee and will be
collected by the
miner who mines your transaction in a block. Although you will receive
priority pro‐
cessing and make a miner very happy, this is probably not what you
intended.
If you forget to add a change output in a manually constructed
transaction, you will be paying the change as a transaction fee.
“Keep the change!” might not be what you intended.
Let’s see how this works in practice, by looking at Alice’s coffee
purchase again. Alice
wants to spend 0.015 bitcoin to pay for coffee. To ensure this transaction
is processed
promptly, she will want to include a transaction fee, say 0.001. That will
mean that the
total cost of the transaction will be 0.016. Her wallet must therefore
source a set of
UTXO that adds up to 0.016 bitcoin or more and, if necessary, create
change. Let’s say
her wallet has a 0.2-bitcoin UTXO available. It will therefore need to
consume this
UTXO, create one output to Bob’s Cafe for 0.015, and a second output with
0.184 bit‐
coin in change back to her own wallet, leaving 0.001 bitcoin unallocated,
as an
implicit fee for the transaction.
Now let’s look at a different scenario. Eugenia, our children’s charity
director in the
Philippines, has completed a fundraiser to purchase schoolbooks for the
children. She
received several thousand small donations from people all around the
world, totaling
50 bitcoin, so her wallet is full of very small payments (UTXO). Now she
wants to
purchase hundreds of schoolbooks from a local publisher, paying in
bitcoin.
As Eugenia’s wallet application tries to construct a single larger payment
transaction,
it must source from the available UTXO set, which is composed of many
smaller
amounts. That means that the resulting transaction will source from more
than a
hundred small-value UTXO as inputs and only one output, paying the book
pub‐
lisher. A transaction with that many inputs will be larger than one
kilobyte, perhaps a
kilobyte or several kilobytes in size. As a result, it will require a much
higher fee than
the median-sized transaction.
Eugenia’s wallet application will calculate the appropriate fee by
measuring the size of
the transaction and multiplying that by the per-kilobyte fee. Many wallets
will over‐
pay fees for larger transactions to ensure the transaction is processed
promptly. The
higher fee is not because Eugenia is spending more money, but because her
transac‐
tion is more complex and larger in size—the fee is independent of the
transaction’s
bitcoin value.
The bitcoin transaction script language, called Script, is a Forth-like
reverse-polish
notation stack-based execution language. If that sounds like gibberish,
you probably
haven’t studied 1960s programming languages, but that’s ok—we will explain
it all in
this chapter. Both the locking script placed on a UTXO and the unlocking
script are
written in this scripting language. When a transaction is validated, the
unlocking
script in each input is executed alongside the corresponding locking
script to see if it
satisfies the spending condition.
Script is a very simple language that was designed to be limited in
scope and exe‐
cutable on a range of hardware, perhaps as simple as an embedded device.
It requires
minimal processing and cannot do many of the fancy things modern
programming
languages can do. For its use in validating programmable money, this is a
deliberate
security feature.
Today, most transactions processed through the bitcoin network have the
form “Pay‐
ment to Bob’s bitcoin address” and are based on a script called a
Pay-to-Public-Key-
Hash script. However, bitcoin transactions are not limited to the “Payment
to Bob’s
bitcoin address” script. In fact, locking scripts can be written to
express a vast variety
of complex conditions. In order to understand these more complex scripts,
we must
first understand the basics of transaction scripts and script language.
In this section, we will demonstrate the basic components of the bitcoin
transaction
scripting language and show how it can be used to express simple
conditions for
spending and how those conditions can be satisfied by unlocking scripts.
Bitcoin transaction validation is not based on a static pattern, but
instead is achieved through the execution of a scripting language.
This language allows for a nearly infinite variety of conditions to be
expressed. This is how bitcoin gets the power of “programmable
money.”
The bitcoin transaction script language contains many operators, but is
deliberately
limited in one important way—there are no loops or complex flow control
capabili‐
ties other than conditional flow control. This ensures that the language
is not Turing
Complete, meaning that scripts have limited complexity and predictable
execution
times. Script is not a general-purpose language. These limitations ensure
that the lan‐
guage cannot be used to create an infinite loop or other form of “logic
bomb” that
could be embedded in a transaction in a way that causes a
denial-of-service attack
against the bitcoin network. Remember, every transaction is validated by
every full
node on the bitcoin network. A limited language prevents the transaction
validation
mechanism from being used as a vulnerability.
The bitcoin transaction script language is stateless, in that there is
no state prior to
execution of the script, or state saved after execution of the script.
Therefore, all the
information needed to execute a script is contained within the script. A
script will
predictably execute the same way on any system. If your system verifies a
script, you
can be sure that every other system in the bitcoin network will also
verify the script,
meaning that a valid transaction is valid for everyone and everyone knows
this. This
predictability of outcomes is an essential benefit of the bitcoin system.
Bitcoin’s transaction validation engine relies on two types of scripts
to validate trans‐
actions: a locking script and an unlocking script.
A locking script is a spending condition placed on an output: it
specifies the condi‐
tions that must be met to spend the output in the future. Historically,
the locking
script was called a scriptPubKey, because it usually contained a public
key or bitcoin
address (public key hash). In this book we refer to it as a “locking
script” to acknowl‐
edge the much broader range of possibilities of this scripting technology.
In most bit‐
coin applications, what we refer to as a locking script will appear in the
source code as
scriptPubKey. You will also see the locking script referred to as a
witness script (see
Appendix D) or more generally as a cryptographic puzzle. These terms all
mean the
same thing, at different levels of abstraction.
An unlocking script is a script that “solves,” or satisfies, the
conditions placed on an
output by a locking script and allows the output to be spent. Unlocking
scripts are
part of every transaction input. Most of the time they contain a digital
signature pro‐
duced by the user’s wallet from his or her private key. Historically, the
unlocking
script was called scriptSig, because it usually contained a digital
signature. In most bit‐
coin applications, the source code refers to the unlocking script as
scriptSig. You
will also see the unlocking script referred to as a witness (see Appendix
D). In this
book, we refer to it as an “unlocking script” to acknowledge the much
broader range
of locking script requirements, because not all unlocking scripts must
contain signa‐
tures.
Every bitcoin validating node will validate transactions by executing
the locking and
unlocking scripts together. Each input contains an unlocking script and
refers to a
previously existing UTXO. The validation software will copy the unlocking
script,
retrieve the UTXO referenced by the input, and copy the locking script
from that
UTXO. The unlocking and locking script are then executed in sequence. The
input is
valid if the unlocking script satisfies the locking script conditions (see
“Separate exe‐
cution of unlocking and locking scripts” on page 136). All the inputs are
validated
independently, as part of the overall validation of the transaction.
Note that the UTXO is permanently recorded in the blockchain, and
therefore is
invariable and is unaffected by failed attempts to spend it by reference
in a new trans‐
action. Only a valid transaction that correctly satisfies the conditions
of the output
results in the output being considered as “spent” and removed from the set
of
unspent transaction outputs (UTXO set).
Малюнок 6-3 є прикладом of the unlocking and locking scripts for
the most common
type of bitcoin transaction (a payment to a public key hash), showing the
combined
script resulting from the concatenation of the unlocking and locking
scripts prior to
script validation.
Малюнок 6-3. Combining scriptSig and scriptPubKey to evaluate a
transaction script
Bitcoin’s scripting language is called a stack-based language because it
uses a data
structure called a stack. A stack is a very simple data structure that can
be visualized
as a stack of cards. A stack allows two operations: push and pop. Push
adds an item
on top of the stack. Pop removes the top item from the stack. Operations
on a stack
can only act on the topmost item on the stack. A stack data structure is
also called a
Last-In-First-Out, or “LIFO” queue.
The scripting language executes the script by processing each item from
left to right.
Numbers (data constants) are pushed onto the stack. Operators push or pop
one or
more parameters from the stack, act on them, and might push a result onto
the stack.
For example, OP_ADD will pop two items from the stack, add them, and push
the
resulting sum onto the stack.
Conditional operators evaluate a condition, producing a boolean result of
TRUE or
FALSE. For example, OP_EQUAL pops two items from the stack and pushes TRUE
(TRUE is represented by the number 1) if they are equal or FALSE
(represented by
zero) if they are not equal. Bitcoin transaction scripts usually contain a
conditional
operator, so that they can produce the TRUE result that signifies a valid
transaction.
Now let’s apply what we’ve learned about scripts and stacks to some
simple examples.
In Малюнок 6-4, the script 2 3 OP_ADD 5 OP_EQUAL demonstrates the
arithmetic addi‐
tion operator OP_ADD, adding two numbers and putting the result on the
stack, fol‐
lowed by the conditional operator OP_EQUAL, which checks that the
resulting sum is
equal to 5. For brevity, the OP_ prefix is omitted in the step-by-step
example. For
more details on the available script operators and functions, see Appendix
B.
Although most locking scripts refer to a public key hash (essentially, a
bitcoin
address), thereby requiring proof of ownership to spend the funds, the
script does not
have to be that complex. Any combination of locking and unlocking scripts
that
results in a TRUE value is valid. The simple arithmetic we used as an
example of the
scripting language is also a valid locking script that can be used to lock
a transaction
output.
Use part of the arithmetic example script as the locking script:
3 OP_ADD 5 OP_EQUAL
which can be satisfied by a transaction containing an input with the
unlocking script:
2
The validation software combines the locking and unlocking scripts and
the resulting
script is:
2 3 OP_ADD 5 OP_EQUAL
As we saw in the step-by-step example in Малюнок 6-4, when this
script is executed, the
result is OP_TRUE, making the transaction valid. Not only is this a valid
transaction
output locking script, but the resulting UTXO could be spent by anyone
with the
arithmetic skills to know that the number 2 satisfies the script.
Transactions are valid if the top result on the stack is TRUE (noted
as {0x01}), any other nonzero value, or if the stack is empty after
script execution. Transactions are invalid if the top value on the
stack is FALSE (a zero-length empty value, noted as {}) or if script
execution is halted explicitly by an operator, such as OP_VERIFY,
OP_RETURN, or a conditional terminator such as OP_ENDIF. See
Appendix B for details.
Малюнок 6-4. Bitcoin’s script validation doing simple math
Transaction Scripts and Script Language
The following is a slightly more complex script, which calculates 2 + 7 —
3 + 1.
Notice that when the script contains several operators in a row, the stack
allows the
results of one operator to be acted upon by the next operator:
2 7 OP_ADD 3 OP_SUB 1 OP_ADD 7 OP_EQUAL
Try validating the preceding script yourself using pencil and paper. When
the script
execution ends, you should be left with the value TRUE on the stack.
Separate execution of unlocking and locking scripts
In the original bitcoin client, the unlocking and locking scripts were
concatenated
and executed in sequence. For security reasons, this was changed in 2010,
because of
a vulnerability that allowed a malformed unlocking script to push data
onto the stack
and corrupt the locking script. In the current implementation, the scripts
are exe‐
cuted separately with the stack transferred between the two executions, as
described
next.
First, the unlocking script is executed, using the stack execution engine.
If the
unlocking script is executed without errors (e.g., it has no “dangling”
operators left
over), the main stack (not the alternate stack) is copied and the locking
script is exe‐
cuted. If the result of executing the locking script with the stack data
copied from the
unlocking script is “TRUE,” the unlocking script has succeeded in
resolving the con‐
ditions imposed by the locking script and, therefore, the input is a valid
authorization
to spend the UTXO. If any result other than “TRUE” remains after execution
of the
combined script, the input is invalid because it has failed to satisfy the
spending con‐
ditions placed on the UTXO.
The vast majority of transactions processed on the bitcoin network spend
outputs
locked with a Pay-to-Public-Key-Hash or “P2PKH” script. These outputs
contain a
locking script that locks the output to a public key hash, more commonly
known as a
bitcoin address. An output locked by a P2PKH script can be unlocked
(spent) by pre‐
senting a public key and a digital signature created by the corresponding
private key
(see “Digital Signatures (ECDSA)” on page 138).
For example, let’s look at Alice’s payment to Bob’s Cafe again. Alice
made a payment
of 0.015 bitcoin to the cafe’s bitcoin address. That transaction output
would have a
locking script of the form:
OP_DUP OP_HASH160 <Cafe Public Key Hash> OP_EQUALVERIFY OP_CHECKSIG
The Cafe Public Key Hash is equivalent to the bitcoin address of the
cafe, without
the Base58Check encoding. Most applications would show the public key hash
in hex‐
adecimal encoding and not the familiar bitcoin address Base58Check format
that
begins with a “1.”
Малюнок 6-6. Evaluating a script for a P2PKH transaction (part 2 of
2)
So far, we have not delved into any detail about “digital signatures.”
In this section we
look at how digital signatures work and how they can present proof of
ownership of a
private key without revealing that private key.
The digital signature algorithm used in bitcoin is the Elliptic Curve
Digital Signature
Algorithm, or ECDSA. ECDSA is the algorithm used for digital signatures
based on
elliptic curve private/public key pairs, as described in “Elliptic Curve
Cryptography
Explained” on page 60. ECDSA is used by the script functions OP_CHECKSIG,
OP_CHECKSIGVERIFY, OP_CHECKMULTISIG, and OP_CHECKMULTISIGVERIFY. Any time
you see those in a locking script, the unlocking script must contain an
ECDSA signa‐
ture.
A digital signature serves three purposes in bitcoin (see the following
sidebar). First,
the signature proves that the owner of the private key, who is by
implication the
owner of the funds, has authorized the spending of those funds. Secondly,
the proof
of authorization is undeniable (nonrepudiation). Thirdly, the signature
proves that
the transaction (or specific parts of the transaction) have not and cannot
be modified
by anyone after it has been signed.
Note that each transaction input is signed independently. This is
critical, as neither
the signatures nor the inputs have to belong to or be applied by the same
“owners.” In
fact, a specific transaction scheme called “CoinJoin” uses this fact to
create multi-
party transactions for privacy.
Each transaction input and any signature it may contain is com‐
pletely independent of any other input or signature. Multiple par‐
ties can collaborate to construct transactions and sign only one
input each.
A digital signature is a mathematical scheme for demonstrating the
authenticity of a
digital message or documents. A valid digital signature gives a recipient
reason to
believe that the message was created by a known sender (authentication),
that the
sender cannot deny having sent the message (nonrepudiation), and that the
message
was not altered in transit (integrity).
Source: https://en.wikipedia.org/wiki/Digital_signature
A digital signature is a mathematical scheme that consists of two parts.
The first part is
an algorithm for creating a signature, using a private key (the signing
key), from a
message (the transaction). The second part is an algorithm that allows
anyone to ver‐
ify the signature, given also the message and a public key.
In bitcoin’s implementation of the ECDSA algorithm, the “message” being
signed is
the transaction, or more accurately a hash of a specific subset of the
data in the trans‐
action (see “Signature Hash Types (SIGHASH)” on page 141). The signing key
is the
user’s private key. The result is the signature:
Sig = F sig Fhash m , dA
where:
• dA is the signing private key
• m is the transaction (or parts of it)
• Fhash is the hashing function
• Fsig is the signing algorithm
• Sig is the resulting signature
More details on the mathematics of ECDSA can be found in “ECDSA Math” on
page
143.
The function Fsig produces a signature Sig that is composed of two values,
commonly
referred to as R and S:
Sig = (R, S)
Now that the two values R and S have been calculated, they are serialized
into a byte-
stream using an international standard encoding scheme called the
Distinguished
Encoding Rules, or DER.
Let’s look at the transaction Alice created again. In the transaction
input there is an
unlocking script that contains the following DER-encoded signature from
Alice’s wal‐
let:
3045022100884d142d86652a3f47ba4746ec719bbfbd040a570b1deccbb6498c75c4ae24cb02204b
9f039ff08df09cbe9f6addac960298cad530a863ea8f53982c09db8f6e381301
That signature is a serialized byte-stream of the R and S values produced
by Alice’s
wallet to prove she owns the private key authorized to spend that output.
The seriali‐
zation format consists of nine elements as follows:
• 0x30—indicating the start of a DER sequence
• 0x45—the length of the sequence (69 bytes)
• 0x02—an integer value follows
• 0x21—the length of the integer (33 bytes)
• R—
00884d142d86652a3f47ba4746ec719bbfbd040a570b1deccbb6498c75c4ae24cb
• 0x02—another integer follows
• 0x20—the length of the integer (32 bytes)
• S—4b9f039ff08df09cbe9f6addac960298cad530a863ea8f53982c09db8f6e3813
• A suffix (0x01) indicating the type of hash used (SIGHASH_ALL)
See if you can decode Alice’s serialized (DER-encoded) signature using
this list. The
important numbers are R and S; the rest of the data is part of the DER
encoding
scheme.
To verify the signature, one must have the signature (R and S), the
serialized transac‐
tion, and the public key (that corresponds to the private key used to
create the signa‐
ture). Essentially, verification of a signature means “Only the owner of
the private key
that generated this public key could have produced this signature on this
transaction.”
The signature verification algorithm takes the message (a hash of the
transaction or
parts of it), the signer’s public key and the signature (R and S values),
and returns
TRUE if the signature is valid for this message and public key.
Digital signatures are applied to messages, which in the case of
bitcoin, are the trans‐
actions themselves. The signature implies a commitment by the signer to
specific
transaction data. In the simplest form, the signature applies to the
entire transaction,
thereby committing all the inputs, outputs, and other transaction fields.
However, a
signature can commit to only a subset of the data in a transaction, which
is useful for
a number of scenarios as we will see in this section.
Bitcoin signatures have a way of indicating which part of a
transaction’s data is
included in the hash signed by the private key using a SIGHASH flag. The
SIGHASH flag
is a single byte that is appended to the signature. Every signature has a
SIGHASH flag
and the flag can be different from to input to input. A transaction with
three signed
inputs may have three signatures with different SIGHASH flags, each
signature signing
(committing) different parts of the transaction.
Remember, each input may contain a signature in its unlocking script. As
a result, a
transaction that contains several inputs may have signatures with
different SIGHASH
flags that commit different parts of the transaction in each of the
inputs. Note also
that bitcoin transactions may contain inputs from different “owners,” who
may sign
only one input in a partially constructed (and invalid) transaction,
collaborating with
others to gather all the necessary signatures to make a valid transaction.
Many of the
SIGHASH flag types only make sense if you think of multiple participants
collaborating
outside the bitcoin network and updating a partially signed transaction.
There are three SIGHASH flags: ALL, NONE, and SINGLE, as shown in Table
6-3.
Table 6-3. SIGHASH types and their meanings
SIGHASH flag Value Description
ALL
0x01
Signature applies to all inputs and outputs
NONE
0x02
Signature applies to all inputs, none of the outputs
SINGLE
0x03
Signature applies to all inputs but only the one output with the
same index number as the signed
input
In addition, there is a modifier flag SIGHASH_ANYONECANPAY, which can be
combined
with each of the preceding flags. When ANYONECANPAY is set, only one input
is signed,
leaving the rest (and their sequence numbers) open for modification. The
ANYONECAN
PAY has the value 0x80 and is applied by bitwise OR, resulting in the
combined flags
as shown in Table 6-4.
Table 6-4. SIGHASH types with modifiers and their meanings
SIGHASH flag
Value Description
ALL|ANYONECANPAY
0x81 Signature applies to one inputs and all outputs
NONE|ANYONECANPAY
0x82
Signature applies to one inputs, none of the outputs
SINGLE|ANYONECANPAY 0x83
Signature applies to one input and the output with the same index number
The way SIGHASH flags are applied during signing and verification is that
a copy of the
transaction is made and certain fields within are truncated (set to zero
length and
emptied). The resulting transaction is serialized. The SIGHASH flag is
added to the end
of the serialized transaction and the result is hashed. The hash itself is
the “message”
that is signed. Depending on which SIGHASH flag is used, different parts
of the trans‐
action are truncated. The resulting hash depends on different subsets of
the data in
the transaction. By including the SIGHASH as the last step before hashing,
the signa‐
ture commits the SIGHASH type as well, so it can’t be changed (e.g., by a
miner).
All SIGHASH types sign the transaction nLocktime field (see “Trans‐
action Locktime (nLocktime)” on page 157). In addition, the SIGH
ASH type itself is appended to the transaction before it is signed, so
that it can’t be modified once signed.
In the example of Alice’s transaction (see the list in “Serialization of
signatures
(DER)” on page 140), we saw that the last part of the DER-encoded
signature was 01,
which is the SIGHASH_ALL flag. This locks the transaction data, so Alice’s
signature is
committing the state of all inputs and outputs. This is the most common
signature
form.
Let’s look at some of the other SIGHASH types and how they can be used in
practice:
ALL|ANYONECANPAY
This construction can be used to make a “crowdfunding”-style transaction.
Someone attempting to raise funds can construct a transaction with a
single out‐
put. The single output pays the “goal” amount to the fundraiser. Such a
transac‐
tion is obviously not valid, as it has no inputs. However, others can now
amend it
by adding an input of their own, as a donation. They sign their own input
with
ALL|ANYONECANPAY. Unless enough inputs are gathered to reach the value of
the
output, the transaction is invalid. Each donation is a “pledge,” which
cannot be
collected by the fundraiser until the entire goal amount is raised.
NONE
This construction can be used to create a “bearer check” or “blank check”
of a
specific amount. It commits to the input, but allows the output locking
script to
be changed. Anyone can write their own bitcoin address into the output
locking
script and redeem the transaction. However, the output value itself is
locked by
the signature.
NONE|ANYONECANPAY
This construction can be used to build a “dust collector.” Users who have
tiny
UTXO in their wallets can’t spend these without the cost in fees exceeding
the
value of the dust. With this type of signature, the dust UTXO can be
donated for
anyone to aggregate and spend whenever they want.
There are some proposals to modify or expand the SIGHASH system. One such
pro‐
posal is Bitmask Sighash Modes by Blockstream’s Glenn Willen, as part of
the Ele‐
ments project. This aims to create a flexible replacement for SIGHASH
types that allows
“arbitrary, miner-rewritable bitmasks of inputs and outputs” that can
express “more
complex contractual precommitment schemes, such as signed offers with
change in a
distributed asset exchange.”
You will not see SIGHASH flags presented as an option in a user’s
wallet application. With few exceptions, wallets construct P2PKH
scripts and sign with SIGHASH_ALL flags. To use a different SIGHASH
flag, you would have to write software to construct and sign trans‐
actions. More importantly, SIGHASH flags can be used by special-
purpose bitcoin applications that enable novel uses.
ECDSA Math
As mentioned previously, signatures are created by a mathematical function
Fsig that
produces a signature composed of two values R and S. In this section we
look at the
function Fsig in more detail.
The signature algorithm first generates an ephemeral (temporary) private
public key
pair. This temporary key pair is used in the calculation of the R and S
values, after a
transformation involving the signing private key and the transaction hash.
The temporary key pair is based on a random number k, which is used as the
tempo‐
rary private key. From k, we generate the corresponding temporary public
key P (cal‐
culated as P = k*G, in the same way bitcoin public keys are derived; see
“Public Keys”
on page 60). The R value of the digital signature is then the x coordinate
of the
ephemeral public key P.
From there, the algorithm calculates the S value of the signature, such
that:
S = k-1 (Hash(m) + dA * R) mod p
where:
• k is the ephemeral private key
• R is the x coordinate of the ephemeral public key
• dA is the signing private key
• m is the transaction data
• p is the prime order of the elliptic curve
Verification is the inverse of the signature generation function, using
the R, S values
and the public key to calculate a value P, which is a point on the
elliptic curve (the
ephemeral public key used in signature creation):
P = S-1 * Hash(m) * G + S-1 * R * Qa
where:
• R and S are the signature values
• Qa is Alice’s public key
• m is the transaction data that was signed
• G is the elliptic curve generator point
If the x coordinate of the calculated point P is equal to R, then the
verifier can con‐
clude that the signature is valid.
Note that in verifying the signature, the private key is neither known nor
revealed.
The math of ECDSA is complex and difficult to understand. There
are a number of great guides online that might help. Search for
“ECDSA explained” or try this one: http://bit.ly/2r0HhGB.
Як ви бачили в розділі “Математика ECDSA”, алгоритм генерації підпису використовує випадковий ключ k, як основу для ефермерної пари з приватного та публічного ключів. Значення k не є важливим, доки воно є випадковим. Якщо одне значення k використовується для виробництва двох сигнатур для різних повідомлень (транзакцій), тоді приватний ключ для підпису може бути обчислений для кожного з них. Повторне використання того ж значення k в алгоритмі підпису дає витік до викриття приватного ключа!
Якщо те саме значення k використовуєтсья в алгоритмі підписування до двох різних транзакцій, приватний ключ може обчислений та викритий перед усім світом!
це не тільки теоретична пожливісь. Ми бачили, як ця проблема призвела до викриття приватних ключів в різних реалізаціях алгоритмів підпису транзакцій буткоін. Люди зтикнулись з викраденням власних коштів через ненавмисне повторне використання значення k. Найбільш важлива причина для повторного використання значення k є невідповідна ініціалізація генератора випадкових чисел.
Щоб уникнути цієї вразливості, найкраща індустріальна практика є відказ від генерування k за допомогою генератора випадкових чисел на базі ентропії, та замість цього використовувати детерміністичний випадковий процес, що базується на даних самої транзакції. Це дає переконання, що кожна транзакція дає продукує інше k. Стандартний індустріальний алгоритм для детермінистичної ініціалізації k визначений в RFC 6979, опублікований Internet Engineering Task Force.
Якщо ви реалізуєте алгоритм для підпису транзакцій в біткоін, ви повинні використовувати RFC 6979, або подібний детермінистично-випадковий алгоритм, щоб бути впевненим, що ви генеруєте інший k для кожної транзакції.
Ми почали цю главу з дослідження, що транзакції виглядають дуже відмінно
“за лаштунками сцени”, на відміну від того, як вони представвляються
гаманцями, переглядачами блокчейну, та іншими користувацькими
застосуваннями. Багато зі спрощених та знайомих концепцій з попередньої
глави, такі, як біткоін адреси та баланси, виглядають відсутніми в
структурі транзакцій. Ми бачили, що транзакції не містять біткоін адрес,
як таких, але замість цього оперують через посередництво скриптів, що
блокують та розблокують окермі вартості біткоіна. Баланси не представлені
будь-де в системі, та досі не кожне застосування гаманця окремо відображує
баланс гаманця користувача.
Тепер, коли ми дослідили, що саме входить в транзакцію біткоін, ми можемо
дослідити, як абстракції верхнього рівня походять від очевидно примітивних
компонент транзакції. Давайте знову подивимось, як транзакція Аліси була
представленою на популярному переглядачеві блоків (Малюнок 6-7).
Малюнок 6-7. Транзакція Аліси в кав'ярні Боба
В лівій частині транзакції переглядач блокчейну показує біткоін адресу Аліси, як “надсилач”. Фактично, ця інформація не міститься в самій транзакції. Коли переглядач блокчейну отримує транзакцію, він також отримує попередню транзакцію, на яку посилаєтсья вхід, та виділяє перший вихід зі старішой транзакції. В цьому виході є блокуючий скрипт, що блокує UTXO хешем публічного ключа Аліси (скрипт P2PKH). Переглядач блокчейну виділяє хеш публічного ключа, та кодує його з використанням кодування Base58Check, щоб спродукувати та відобразити біткоін адресу, що представляє публічний ключ.
Подібно до цього, в правій стороні переглядач блокчейну показує два
виходи; перший до біткоін адреси Боба, та другий не біткоін адресу Аліси
(як решта). Ще раз, щоб створити ці адреси біткоін, переглядач блокчейну
викреслив блокуючий скрипт для кожного виходу, розпізнав P2PKH скрипт, та
виділив з нього хеш публічного ключа. Нарешті, переглядач блокчейну
перекодував цей публічний ключ за допомогою Base58Check, щоб спродукувати
та відобразити адреси біткоін. Якщо ви клацнете на адресі біткоіна Боба,
переглядач блокчейну покаже вам дещо, подібне до Малюнка 6-8.
Малюнок 6-8. Баланс біткоін адреси Боба
Переглядач біткоін відображує баланс адреси біткоін Боба. Але ніде в
системі біткоін немає концепції “балансу”. Скоріше, значення, відображені
тут, сконструйовані переглядачем блокчейна, як показане нижче.
Щоб побудувати суму “Загально отримано” (Final Balance), переглядач
блокчейну зпершу буде декодувати кодування Base58Check адреси біткоіну,
щоб отримати 160-бітний хеш бобівського публічного ключа, що закодований в
адресі. Потім переглядач блокчейну буде шукати в базі даних транзакцій,
шукаючи виходи з блокуючими скриптами P2PKH, що містять хеш публічного
ключа Бота. Через складання значень всіх виходів переглядач блокчейну може
спродукувати загальну отриману суму.
Конструювання поточного балансу (відображується як “Final Balance”)
потребує трохи більше роботи. Переглядач блокчейну має окрему базу даних
віходів, що наразі не витрачені, тобто набір UTXO. Щоб підтримувати цю
базу даних, переглядач блокчейну має мониторити мережу біткоін, додавати
нові створені UTXO, та видаляти витрачені UTXO, в реальному часі, по мірі
того, як вони з'являються в непідтверджених транзакціях. Це складний
процес, що залежить від відсліджування транзакцій по мірі їх просування,
так само, як обслуговування консенсусу мережі біткоіну, щоб переконатись,
що ми слідуємо коректному відгалуженню ланцюга. Іноді переглядач блокчейну
розсинхронізується, та його персектива на набір UTXO наповна або
некоректна.
З набору UTXO переглядач блокчейну підсумовує вартість всіх невитрачених
виходів, що посилаються на публічний ключ Боба, та продукують “остаточний
баланс”, число, що показується користувачему.
Щоб спродукувати один цей образ з двома “балансами” переглядач блокчейну
має індексувати та шукати часом десятки, сотні, або часом і сотні тисяч
транзакцій.
Підсумовуючи, інформація, що представляється користувачеву через
застосування гаманця, переглядачі блокчейну, або інші користувацькі
інтерфейси біткоіну, часто є компонуванням високорівневих абстракцій, що
походять від сканування багатьох різних транзакцій, пеервірки їх вмісту,
та маніпуляцій даними, що там містяться. Через презентування цього
спрощеного погляду на трензакції біткоін, що копіюють банківські чеки від
одного надсилача до одного отримувача, ці застосування мають
абстрагуватись від багатьох підлеглих деталей. Вони в основному
фокусуються на загальних типах транзакцій: P2PKH з сигнатурами SIGHASH_ALL
на кожному вході. Таким чином, хоча застосування біткоіну можуть
представляти більше ніж 80% з усіх транзакцій в просто-читаємій манері,
вони часом плутаються в транзакціях, що відхиляються від норми.
Транзакції, що містять більш складні блокуючі скрипти, або інші флаги
SIGHASH, або багато входів та виходів, демонструють простоту та слабкість
ціх абстракцій.
Кожного дня сотні транзакцій, що не містять виходів P2PKH, отримують підтвердження блокчейну. Переглядачі блокчейну часто представляють їх з червоними повідомленнями попереджень, які кажуть, що адресу неможливо декодувати. Наступне посилання містить найпізніші “дивні транзакції”, що не були повністю декодовані:
https://blockchain.info/strange-transactions.
Як ми бачили в попередній главі, це не обов'язково дивні транзакції. Це
транзакції, що містять більш складні блокуючі скрипти, ніж загальні P2PKH.
Ми вивчимо щодо декодування та розуміння більш складних скриптів, та про
застосування, що використовують їх, трохи далі.
In the previous chapter, we introduced the basic elements of bitcoin
transactions and
looked at the most common type of transaction script, the P2PKH script. In
this
chapter we will look at more advanced scripting and how we can use it to
build trans‐
actions with complex conditions.
First, we will look at multisignature scripts. Next, we will examine the
second most
common transaction script, Pay-to-Script-Hash, which opens up a whole
world of
complex scripts. Then, we will examine new script operators that add a
time dimen‐
sion to bitcoin, through timelocks.
Multisignature scripts set a condition where N public keys are recorded
in the script
and at least M of those must provide signatures to unlock the funds. This
is also
known as an M-of-N scheme, where N is the total number of keys and M is
the thres‐
hold of signatures required for validation. For example, a 2-of-3
multisignature is one
where three public keys are listed as potential signers and at least two
of those must
be used to create signatures for a valid transaction to spend the funds.
At this time,
standard multisignature scripts are limited to at most 15 listed public
keys, meaning
you can do anything from a 1-of-1 to a 15-of-15 multisignature or any
combination
within that range. The limitation to 15 listed keys might be lifted by the
time this
book is published, so check the isStandard() function to see what is
currently
accepted by the network.
The general form of a locking script setting an M-of-N multisignature
condition is:
M <Public Key 1> <Public Key 2> ... <Public Key N> N
CHECKMULTISIG
where N is the total number of listed public keys and M is the threshold
of required
signatures to spend the output.
A locking script setting a 2-of-3 multisignature condition looks like
this:
2 <Public Key A> <Public Key B> <Public Key C> 3
CHECKMULTISIG
The preceding locking script can be satisfied with an unlocking script
containing
pairs of signatures and public keys:
<Signature B> <Signature C>
or any combination of two signatures from the private keys corresponding
to the
three listed public keys.
The two scripts together would form the combined validation script:
<Signature B> <Signature C> 2 <Public Key A> <Public
Key B> <Public Key C> 3
CHECKMULTISIG
When executed, this combined script will evaluate to TRUE if, and only
if, the
unlocking script matches the conditions set by the locking script. In this
case, the
condition is whether the unlocking script has a valid signature from the
two private
keys that correspond to two of the three public keys set as an
encumbrance.
There is a bug in CHECKMULTISIG’s execution that requires a slight
workaround. When
CHECKMULTISIG executes, it should consume M+N+2 items on the stack as
parame‐
ters. However, due to the bug, CHECKMULTISIG will pop an extra value or
one value
more than expected.
Let’s look at this in greater detail using the previous validation
example:
<Signature B> <Signature C> 2 <Public Key A> <Public
Key B> <Public Key C> 3
CHECKMULTISIG
First, CHECKMULTISIG pops the top item, which is N (in this example “3”).
Then it pops
N items, which are the public keys that can sign. In this example, public
keys A, B, and
C. Then, it pops one item, which is M, the quorum (how many signatures are
needed).
Here M = 2. At this point, CHECKMULTISIG should pop the final M items,
which are the
signatures, and see if they are valid. However, unfortunately, a bug in
the implemen‐
tation causes CHECKMULTISIG to pop one more item (M+1 total) than it
should. The
extra item is disregarded when checking the signatures so it has no direct
effect on
CHECKMULTISIG itself. However, an extra value must be present because if
it is not
present, when CHECKMULTISIG attempts to pop on an empty stack, it will
cause a stack
error and script failure (marking the transaction as invalid). Because the
extra item is
disregarded it can be anything, but customarily 0 is used.
in every full node, until it was spent. All of these issues make using
complex locking
scripts difficult in practice.
P2SH was developed to resolve these practical difficulties and to make the
use of
complex scripts as easy as a payment to a bitcoin address. With P2SH
payments, the
complex locking script is replaced with its digital fingerprint, a
cryptographic hash.
When a transaction attempting to spend the UTXO is presented later, it
must contain
the script that matches the hash, in addition to the unlocking script. In
simple terms,
P2SH means “pay to a script matching this hash, a script that will be
presented later
when this output is spent.”
In P2SH transactions, the locking script that is replaced by a hash is
referred to as the
redeem script because it is presented to the system at redemption time
rather than as a
locking script. Table 7-1 shows the script without P2SH and Table 7-2
shows the same
script encoded with P2SH.
Table 7-1. Complex script without P2SH
Locking Script
2 PubKey1 PubKey2 PubKey3 PubKey4 PubKey5 5 CHECKMULTISIG
Unlocking Script Sig1 Sig2
Table 7-2. Complex script as P2SH
Redeem Script
2 PubKey1 PubKey2 PubKey3 PubKey4 PubKey5 5 CHECKMULTISIG
Locking Script
HASH160 <20-byte hash of redeem script> EQUAL
Unlocking Script Sig1 Sig2 <redeem script>
As you can see from the tables, with P2SH the complex script that details
the condi‐
tions for spending the output (redeem script) is not presented in the
locking script.
Instead, only a hash of it is in the locking script and the redeem script
itself is presen‐
ted later, as part of the unlocking script when the output is spent. This
shifts the bur‐
den in fees and complexity from the sender to the recipient (spender) of
the
transaction.
Let’s look at Mohammed’s company, the complex multisignature script, and
the
resulting P2SH scripts.
First, the multisignature script that Mohammed’s company uses for all
incoming pay‐
ments from customers:
2 <Mohammed's Public Key> <Partner1 Public Key> <Partner2
Public Key> <Partner3
Public Key> <Attorney Public Key> 5 CHECKMULTISIG
If the placeholders are replaced by actual public keys (shown here as
520-bit numbers
starting with 04) you can see that this script becomes very long:
152
|
Chapter 7: Advanced Transactions and Scripting
2
04C16B8698A9ABF84250A7C3EA7EEDEF9897D1C8C6ADF47F06CF73370D74DCCA01CDCA79DCC5C395
D7EEC6984D83F1F50C900A24DD47F569FD4193AF5DE762C58704A2192968D8655D6A935BEAF2CA23
E3FB87A3495E7AF308EDF08DAC3C1FCBFC2C75B4B0F4D0B1B70CD2423657738C0C2B1D5CE65C97D7
8D0E34224858008E8B49047E63248B75DB7379BE9CDA8CE5751D16485F431E46117B9D0C1837C9D5
737812F393DA7D4420D7E1A9162F0279CFC10F1E8E8F3020DECDBC3C0DD389D99779650421D65CBD
7149B255382ED7F78E946580657EE6FDA162A187543A9D85BAAA93A4AB3A8F044DADA618D0872274
40645ABE8A35DA8C5B73997AD343BE5C2AFD94A5043752580AFA1ECED3C68D446BCAB69AC0BA7DF5
0D56231BE0AABF1FDEEC78A6A45E394BA29A1EDF518C022DD618DA774D207D137AAB59E0B000EB7E
D238F4D800 5 CHECKMULTISIG
This entire script can instead be represented by a 20-byte cryptographic
hash, by first
applying the SHA256 hashing algorithm and then applying the RIPEMD160
algo‐
rithm on the result. The 20-byte hash of the preceding script is:
54c557e07dde5bb6cb791c7a540e0a4796f5e97e
A P2SH transaction locks the output to this hash instead of the longer
script, using
the locking script:
HASH160 54c557e07dde5bb6cb791c7a540e0a4796f5e97e EQUAL
which, as you can see, is much shorter. Instead of “pay to this 5-key
multisignature
script,” the P2SH equivalent transaction is “pay to a script with this
hash.” A customer
making a payment to Mohammed’s company need only include this much shorter
locking script in his payment. When Mohammed and his partners want to
spend this
UTXO, they must present the original redeem script (the one whose hash
locked the
UTXO) and the signatures necessary to unlock it, like this:
<Sig1> <Sig2> <2 PK1 PK2 PK3 PK4 PK5 5 CHECKMULTISIG>
The two scripts are combined in two stages. First, the redeem script is
checked
against the locking script to make sure the hash matches:
<2 PK1 PK2 PK3 PK4 PK5 5 CHECKMULTISIG> HASH160 <redeem
scriptHash> EQUAL
If the redeem script hash matches, the unlocking script is executed on its
own, to
unlock the redeem script:
<Sig1> <Sig2> 2 PK1 PK2 PK3 PK4 PK5 5 CHECKMULTISIG
Almost all the scripts described in this chapter can only be implemented
as P2SH
scripts. They cannot be used directly in the locking script of a UTXO.
P2SH Addresses
Another important part of the P2SH feature is the ability to encode a
script hash as an
address, as defined in BIP-13. P2SH addresses are Base58Check encodings of
the 20-
byte hash of a script, just like bitcoin addresses are Base58Check
encodings of the 20-
byte hash of a public key. P2SH addresses use the version prefix “5,”
which results in
Base58Check-encoded addresses that start with a “3.” For example,
Mohammed’s
Pay-to-Script-Hash (P2SH)
|
153
complex script, hashed and Base58Check-encoded as a P2SH address, becomes
39RF6JqABiHdYHkfChV6USGMe6Nsr66Gzw. Now, Mohammed can give this “address”
to
his customers and they can use almost any bitcoin wallet to make a simple
payment,
as if it were a bitcoin address. The 3 prefix gives them a hint that this
is a special type
of address, one corresponding to a script instead of a public key, but
otherwise it
works in exactly the same way as a payment to a bitcoin address.
P2SH addresses hide all of the complexity, so that the person making a
payment does
not see the script.
Benefits of P2SH
The P2SH feature offers the following benefits compared to the direct use
of complex
scripts in locking outputs:
• Complex scripts are replaced by shorter fingerprints in the transaction
output,
making the transaction smaller.
• Scripts can be coded as an address, so the sender and the sender’s
wallet don’t
need complex engineering to implement P2SH.
• P2SH shifts the burden of constructing the script to the recipient, not
the sender.
• P2SH shifts the burden in data storage for the long script from the
output (which
is in the UTXO set) to the input (stored on the blockchain).
• P2SH shifts the burden in data storage for the long script from the
present time
(payment) to a future time (when it is spent).
• P2SH shifts the transaction fee cost of a long script from the sender to
the recipi‐
ent, who has to include the long redeem script to spend it.
Redeem Script and Validation
Prior to version 0.9.2 of the Bitcoin Core client, Pay-to-Script-Hash was
limited to the
standard types of bitcoin transaction scripts, by the isStandard()
function. That
means that the redeem script presented in the spending transaction could
only be one
of the standard types: P2PK, P2PKH, or multisig nature, excluding RETURN
and P2SH
itself.
As of version 0.9.2 of the Bitcoin Core client, P2SH transactions can
contain any valid
script, making the P2SH standard much more flexible and allowing for
experimenta‐
tion with many novel and complex types of transactions.
Note that you are not able to put a P2SH inside a P2SH redeem script,
because the
P2SH specification is not recursive. While it is technically possible to
include RETURN
in a redeem script, as nothing in the rules prevents you from doing so, it
is of no
154
|
Chapter 7: Advanced Transactions and Scripting
practical use because executing RETURN during validation will cause the
transaction to
be marked invalid.
Note that because the redeem script is not presented to the network until
you attempt
to spend a P2SH output, if you lock an output with the hash of an invalid
redeem
script it will be processed regardless. The UTXO will be successfully
locked. However,
you will not be able to spend it because the spending transaction, which
includes the
redeem script, will not be accepted because it is an invalid script. This
creates a risk,
because you can lock bitcoin in a P2SH that cannot be spent later. The
network will
accept the P2SH locking script even if it corresponds to an invalid redeem
script,
because the script hash gives no indication of the script it represents.
P2SH locking scripts contain the hash of a redeem script, which
gives no clues as to the content of the redeem script itself. The
P2SH transaction will be considered valid and accepted even if the
redeem script is invalid. You might accidentally lock bitcoin in such
a way that it cannot later be spent.
Data Recording Output (RETURN)
Bitcoin’s distributed and timestamped ledger, the blockchain, has
potential uses far
beyond payments. Many developers have tried to use the transaction
scripting lan‐
guage to take advantage of the security and resilience of the system for
applications
such as digital notary services, stock certificates, and smart contracts.
Early attempts
to use bitcoin’s script language for these purposes involved creating
transaction out‐
puts that recorded data on the blockchain; for example, to record a
digital fingerprint
of a file in such a way that anyone could establish proof-of-existence of
that file on a
specific date by reference to that transaction.
The use of bitcoin’s blockchain to store data unrelated to bitcoin
payments is a con‐
troversial subject. Many developers consider such use abusive and want to
discourage
it. Others view it as a demonstration of the powerful capabilities of
blockchain tech‐
nology and want to encourage such experimentation. Those who object to the
inclu‐
sion of nonpayment data argue that it causes “blockchain bloat,” burdening
those
running full bitcoin nodes with carrying the cost of disk storage for data
that the
blockchain was not intended to carry. Moreover, such transactions create
UTXO that
cannot be spent, using the destination bitcoin address as a freeform
20-byte field.
Because the address is used for data, it doesn’t correspond to a private
key and the
resulting UTXO can never be spent; it’s a fake payment. These transactions
that can
never be spent are therefore never removed from the UTXO set and cause the
size of
the UTXO database to forever increase, or “bloat.”
In version 0.9 of the Bitcoin Core client, a compromise was reached with
the intro‐
duction of the RETURN operator. RETURN allows developers to add 80 bytes
of nonpay‐
Data Recording Output (RETURN)
|
155
ment data to a transaction output. However, unlike the use of “fake” UTXO,
the
RETURN operator creates an explicitly provably unspendable output, which
does not
need to be stored in the UTXO set. RETURN outputs are recorded on the
blockchain,
so they consume disk space and contribute to the increase in the
blockchain’s size, but
they are not stored in the UTXO set and therefore do not bloat the UTXO
memory
pool and burden full nodes with the cost of more expensive RAM.
RETURN scripts look like this:
RETURN <data>
The data portion is limited to 80 bytes and most often represents a hash,
such as the
output from the SHA256 algorithm (32 bytes). Many applications put a
prefix in front
of the data to help identify the application. For example, the Proof of
Existence digital
notarization service uses the 8-byte prefix DOCPROOF, which is ASCII
encoded as 44
4f 43 50 52 4f 4f 46 in hexadecimal.
Keep in mind that there is no “unlocking script” that corresponds to
RETURN that
could possibly be used to “spend” a RETURN output. The whole point of
RETURN is that
you can’t spend the money locked in that output, and therefore it does not
need to be
held in the UTXO set as potentially spendable—RETURN is provably
unspendable.
RETURN is usually an output with a zero bitcoin amount, because any
bitcoin assigned
to such an output is effectively lost forever. If a RETURN is referenced
as an input in a
transaction, the script validation engine will halt the execution of the
validation script
and mark the transaction as invalid. The execution of RETURN essentially
causes the
script to “RETURN” with a FALSE and halt. Thus, if you accidentally
reference a
RETURN output as an input in a transaction, that transaction is invalid.
A standard transaction (one that conforms to the isStandard() checks) can
have
only one RETURN output. However, a single RETURN output can be combined in
a
transaction with outputs of any other type.
Two new command-line options have been added in Bitcoin Core as of version
0.10.
The option datacarrier controls relay and mining of RETURN transactions,
with the
default set to “1” to allow them. The option datacarriersize takes a
numeric argu‐
ment specifying the maximum size in bytes of the RETURN script, 83 bytes
by default,
which, allows for a maximum of 80 bytes of RETURN data plus one byte of
RETURN
opcode and two bytes of PUSHDATA opcode.
RETURN was initially proposed with a limit of 80 bytes, but the limit
was reduced to 40 bytes when the feature was released. In February
2015, in version 0.10 of Bitcoin Core, the limit was raised back to
80 bytes. Nodes may choose not to relay or mine RETURN, or only
relay and mine RETURN containing less than 80 bytes of data.
156
| Chapter 7: Advanced Transactions and Scripting
Timelocks
Timelocks are restrictions on transactions or outputs that only allow
spending after a
point in time. Bitcoin has had a transaction-level timelock feature from
the begin‐
ning. It is implemented by the nLocktime field in a transaction. Two new
timelock
features were introduced in late 2015 and mid-2016 that offer UTXO-level
timelocks.
These are CHECKLOCKTIMEVERIFY and CHECKSEQUENCEVERIFY.
Timelocks are useful for postdating transactions and locking funds to a
date in the
future. More importantly, timelocks extend bitcoin scripting into the
dimension of
time, opening the door for complex multistep smart contracts.
Transaction Locktime (nLocktime)
From the beginning, bitcoin has had a transaction-level timelock feature.
Transaction
locktime is a transaction-level setting (a field in the transaction data
structure) that
defines the earliest time that a transaction is valid and can be relayed
on the network
or added to the blockchain. Locktime is also known as nLocktime from the
variable
name used in the Bitcoin Core codebase. It is set to zero in most
transactions to indi‐
cate immediate propagation and execution. If nLocktime is nonzero and
below 500
million, it is interpreted as a block height, meaning the transaction is
not valid and is
not relayed or included in the blockchain prior to the specified block
height. If it is
above 500 million, it is interpreted as a Unix Epoch timestamp (seconds
since
Jan-1-1970) and the transaction is not valid prior to the specified time.
Transactions
with nLocktime specifying a future block or time must be held by the
originating sys‐
tem and transmitted to the bitcoin network only after they become valid.
If a transac‐
tion is transmitted to the network before the specified nLocktime, the
transaction will
be rejected by the first node as invalid and will not be relayed to other
nodes. The use
of nLocktime is equivalent to postdating a paper check.
Transaction locktime limitations
nLocktime has the limitation that while it makes it possible to spend some
outputs in
the future, it does not make it impossible to spend them until that time.
Let’s explain
that with the following example.
Alice signs a transaction spending one of her outputs to Bob’s address,
and sets the
transaction nLocktime to 3 months in the future. Alice sends that
transaction to Bob
to hold. With this transaction Alice and Bob know that:
• Bob cannot transmit the transaction to redeem the funds until 3 months
have
elapsed.
• Bob may transmit the transaction after 3 months.
Timelocks
|
157
However:
• Alice can create another transaction, double-spending the same inputs
without a
locktime. Thus, Alice can spend the same UTXO before the 3 months have
elapsed.
• Bob has no guarantee that Alice won’t do that.
It is important to understand the limitations of transaction nLocktime.
The only
guarantee is that Bob will not be able to redeem it before 3 months have
elapsed.
There is no guarantee that Bob will get the funds. To achieve such a
guarantee, the
timelock restriction must be placed on the UTXO itself and be part of the
locking
script, rather than on the transaction. This is achieved by the next form
of timelock,
called Check Lock Time Verify.
Check Lock Time Verify (CLTV)
In December 2015, a new form of timelock was introduced to bitcoin as a
soft fork
upgrade. Based on a specifications in BIP-65, a new script operator called
CHECK‐
LOCKTIMEVERIFY (CLTV) was added to the scripting language. CLTV is a per-
output timelock, rather than a per-transaction timelock as is the case
with nLocktime.
This allows for much greater flexibility in the way timelocks are applied.
In simple terms, by adding the CLTV opcode in the redeem script of an
output it
restricts the output, so that it can only be spent after the specified
time has elapsed.
While nLocktime is a transaction-level timelock, CLTV is an output-
based timelock.
CLTV doesn’t replace nLocktime, but rather restricts specific UTXO such
that they can
only be spent in a future transaction with nLocktime set to a greater or
equal value.
The CLTV opcode takes one parameter as input, expressed as a number in the
same
format as nLocktime (either a block height or Unix epoch time). As
indicated by the
VERIFY suffix, CLTV is the type of opcode that halts execution of the
script if the out‐
come is FALSE. If it results in TRUE, execution continues.
In order to lock an output with CLTV, you insert it into the redeem script
of the out‐
put in the transaction that creates the output. For example, if Alice is
paying Bob’s
address, the output would normally contain a P2PKH script like this:
DUP HASH160 <Bob's Public Key Hash> EQUALVERIFY CHECKSIG
158
|
Chapter 7: Advanced Transactions and Scripting
To lock it to a time, say 3 months from now, the transaction would be a
P2SH trans‐
action with a redeem script like this:
<now + 3 months> CHECKLOCKTIMEVERIFY DROP DUP HASH160 <Bob's
Public Key Hash>
EQUALVERIFY CHECKSIG
where <now + 3 months> is a block height or time value estimated 3
months from the
time the transaction is mined: current block height + 12,960 (blocks) or
current Unix
epoch time + 7,760,000 (seconds). For now, don’t worry about the DROP
opcode that
follows CHECKLOCKTIMEVERIFY; it will be explained shortly.
When Bob tries to spend this UTXO, he constructs a transaction that
references the
UTXO as an input. He uses his signature and public key in the unlocking
script of
that input and sets the transaction nLocktime to be equal or greater to
the timelock in
the CHECKLOCKTIMEVERIFY Alice set. Bob then broadcasts the transaction on
the bit‐
coin network.
Bob’s transaction is evaluated as follows. If the CHECKLOCKTIMEVERIFY
parameter Alice
set is less than or equal the spending transaction’s nLocktime, script
execution contin‐
ues (acts as if a “no operation” or NOP opcode was executed). Otherwise,
script exe‐
cution halts and the transaction is deemed invalid.
More precisely, CHECKLOCKTIMEVERIFY fails and halts execution, marking the
transac‐
tion invalid if (source: BIP-65):
1. the stack is empty; or
2. the top item on the stack is less than 0; or
3. the lock-time type (height versus timestamp) of the top stack item and
the nLock
time field are not the same; or
4. the top stack item is greater than the transaction’s nLocktime field;
or
5. the nSequence field of the input is 0xffffffff.
CLTV and nLocktime use the same format to describe timelocks,
either a block height or the time elapsed in seconds since Unix
epoch. Critically, when used together, the format of nLocktime
must match that of CLTV in the inputs—they must both reference
either block height or time in seconds.
After execution, if CLTV is satisfied, the time parameter that preceded it
remains as the
top item on the stack and may need to be dropped, with DROP, for correct
execution
of subsequent script opcodes. You will often see CHECKLOCKTIMEVERIFY
followed by
DROP in scripts for this reason.
Timelocks
|
159
By using nLocktime in conjunction with CLTV, the scenario described in
“Transaction
locktime limitations” on page 157 changes. Because Alice locked the UTXO
itself, it is
now impossible for either Bob or Alice to spend it before the 3-month
locktime has
expired.
By introducing timelock functionality directly into the scripting
language, CLTV
allows us to develop some very interesting complex scripts.
The standard is defined in BIP-65 (CHECKLOCKTIMEVERIFY).
Relative Timelocks
nLocktime and CLTV are both absolute timelocks in that they specify an
absolute point
in time. The next two timelock features we will examine are relative
timelocks in that
they specify, as a condition of spending an output, an elapsed time from
the confir‐
mation of the output in the blockchain.
Relative timelocks are useful because they allow a chain of two or more
interdepend‐
ent transactions to be held off chain, while imposing a time constraint on
one trans‐
action that is dependent on the elapsed time from the confirmation of a
previous
transaction. In other words, the clock doesn’t start counting until the
UTXO is recor‐
ded on the blockchain. This functionality is especially useful in
bidirectional state
channels and Lightning Networks, as we will see in “Payment Channels and
State
Channels” on page 284.
Relative timelocks, like absolute timelocks, are implemented with both a
transaction-
level feature and a script-level opcode. The transaction-level relative
timelock is
implemented as a consensus rule on the value of nSequence, a transaction
field that is
set in every transaction input. Script-level relative timelocks are
implemented with
the CHECKSEQUENCEVERIFY (CSV) opcode.
Relative timelocks are implemented according to the specifications in
BIP-68, Rela‐
tive lock-time using consensus-enforced sequence numbers and BIP-112,
CHECKSE‐
QUENCEVERIFY.
BIP-68 and BIP-112 were activated in May 2016 as a soft fork upgrade to
the consen‐
sus rules.
Relative Timelocks with nSequence
Relative timelocks can be set on each input of a transaction, by setting
the nSequence
field in each input.
Original meaning of nSequence
The nSequence field was originally intended (but never properly
implemented) to
allow modification of transactions in the mempool. In that use, a
transaction contain‐
160
|
Chapter 7: Advanced Transactions and Scripting
ing inputs with nSequence value below 232 (0xFFFFFFFF) indicated a
transaction that
was not yet “finalized.” Such a transaction would be held in the mempool
until it was
replaced by another transaction spending the same inputs with a higher
nSequence
value. Once a transaction was received whose inputs had an nSequence value
of 232 it
would be considered “finalized” and mined.
The original meaning of nSequence was never properly implemented and the
value of
nSequence is customarily set to 232 in transactions that do not utilize
timelocks. For
transactions with nLocktime or CHECKLOCKTIMEVERIFY, the nSequence value
must be
set to less than 232 for the timelock guards to have effect. Customarily,
it is set to
232 – 1 (0xFFFFFFFE).
nSequence as a consensus-enforced relative timelock
Since the activation of BIP-68, new consensus rules apply for any
transaction contain‐
ing an input whose nSequence value is less than 231 (bit 1<<31 is
not set). Program‐
matically, that means that if the most significant (bit 1<<31) is
not set, it is a flag that
means “relative locktime.” Otherwise (bit 1<<31 set), the nSequence
value is reserved
for other uses such as enabling CHECKLOCKTIMEVERIFY, nLocktime,
Opt-In-Replace-
By-Fee, and other future developments.
Transaction inputs with nSequence values less than 231 are interpreted as
having a rel‐
ative timelock. Such a transaction is only valid once the input has aged
by the relative
timelock amount. For example, a transaction with one input with an
nSequence rela‐
tive timelock of 30 blocks is only valid when at least 30 blocks have
elapsed from the
time the UTXO referenced in the input was mined. Since nSequence is a
per-input
field, a transaction may contain any number of timelocked inputs, all of
which must
have sufficiently aged for the transaction to be valid. A transaction can
include both
timelocked inputs (nSequence < 231) and inputs without a relative
timelock (nSe
quence >= 231).
The nSequence value is specified in either blocks or seconds, but in a
slightly different
format than we saw used in nLocktime. A type-flag is used to differentiate
between
values counting blocks and values counting time in seconds. The type-flag
is set in
the 23rd least-significant bit (i.e., value 1<<22). If the type-flag
is set, then the nSe
quence value is interpreted as a multiple of 512 seconds. If the type-flag
is not set, the
nSequence value is interpreted as a number of blocks.
When interpreting nSequence as a relative timelock, only the 16 least
significant bits
are considered. Once the flags (bits 32 and 23) are evaluated, the
nSequence value is
usually “masked” with a 16-bit mask (e.g., nSequence & 0x0000FFFF).
Малюнок 7-1 shows the binary layout of the nSequence value, as
defined by BIP-68.
Timelocks
|
161
Малюнок 7-1. BIP-68 definition of nSequence encoding (Source:
BIP-68)
Relative timelocks based on consensus enforcement of the nSequence value
are
defined in BIP-68.
The standard is defined in BIP-68, Relative lock-time using
consensus-enforced
sequence numbers.
Relative Timelocks with CSV
Just like CLTV and nLocktime, there is a script opcode for relative
timelocks that lev‐
erages the nSequence value in scripts. That opcode is CHECKSEQUENCEVERIFY,
com‐
monly referred to as CSV for short.
The CSV opcode when evaluated in a UTXO’s redeem script allows spending
only in a
transaction whose input nSequence value is greater than or equal to the
CSV parame‐
ter. Essentially, this restricts spending the UTXO until a certain number
of blocks or
seconds have elapsed relative to the time the UTXO was mined.
As with CLTV, the value in CSV must match the format in the corresponding
nSe
quence value. If CSV is specified in terms of blocks, then so must
nSequence. If CSV is
specified in terms of seconds, then so must nSequence.
Relative timelocks with CSV are especially useful when several (chained)
transactions
are created and signed, but not propagated, when they’re kept “off-chain.”
A child
transaction cannot be used until the parent transaction has been
propagated, mined,
and aged by the time specified in the relative timelock. One application
of this use
case can be seen in “Payment Channels and State Channels” on page 284 and
“Routed
Payment Channels (Lightning Network)” on page 297.
CSV is defined in detail in BIP-112, CHECKSEQUENCEVERIFY.
Median-Time-Past
As part of the activation of relative timelocks, there was also a change
in the way
“time” is calculated for timelocks (both absolute and relative). In
bitcoin there is a
subtle, but very significant, difference between wall time and consensus
time. Bitcoin
162
|
Chapter 7: Advanced Transactions and Scripting
is a decentralized network, which means that each participant has his or
her own per‐
spective of time. Events on the network do not occur instantaneously
everywhere.
Network latency must be factored into the perspective of each node.
Eventually
everything is synchronized to create a common ledger. Bitcoin reaches
consensus
every 10 minutes about the state of the ledger as it existed in the past.
The timestamps set in block headers are set by the miners. There is a
certain degree of
latitude allowed by the consensus rules to account for differences in
clock accuracy
between decentralized nodes. However, this creates an unfortunate
incentive for min‐
ers to lie about the time in a block so as to earn extra fees by including
timelocked
transactions that are not yet mature. See the following section for more
information.
To remove the incentive to lie and strengthen the security of timelocks, a
BIP was
proposed and activated at the same time as the BIPs for relative
timelocks. This is
BIP-113, which defines a new consensus measurement of time called
Median-Time-
Past.
Median-Time-Past is calculated by taking the timestamps of the last 11
blocks and
finding the median. That median time then becomes consensus time and is
used for
all timelock calculations. By taking the midpoint from approximately two
hours in
the past, the influence of any one block’s timestamp is reduced. By
incorporating 11
blocks, no single miner can influence the timestamps in order to gain fees
from trans‐
actions with a timelock that hasn’t yet matured.
Median-Time-Past changes the implementation of time calculations for
nLocktime,
CLTV, nSequence, and CSV. The consensus time calculated by
Median-Time-Past is
always approximately one hour behind wall clock time. If you create
timelock trans‐
actions, you should account for it when estimating the desired value to
encode in
nLocktime, nSequence, CLTV, and CSV.
Median-Time-Past is specified in BIP-113.
Timelock Defense Against Fee Sniping
Fee-sniping is a theoretical attack scenario, where miners attempting to
rewrite past
blocks “snipe” higher-fee transactions from future blocks to maximize
their profita‐
bility.
For example, let’s say the highest block in existence is block #100,000.
If instead of
attempting to mine block #100,001 to extend the chain, some miners attempt
to
remine #100,000. These miners can choose to include any valid transaction
(that
hasn’t been mined yet) in their candidate block #100,000. They don’t have
to remine
the block with the same transactions. In fact, they have the incentive to
select the
most profitable (highest fee per kB) transactions to include in their
block. They can
include any transactions that were in the “old” block #100,000, as well as
any transac‐
Timelocks
|
163
tions from the current mempool. Essentially they have the option to pull
transactions
from the “present” into the rewritten “past” when they re-create block
#100,000.
Today, this attack is not very lucrative, because block reward is much
higher than
total fees per block. But at some point in the future, transaction fees
will be the
majority of the reward (or even the entirety of the reward). At that time,
this scenario
becomes inevitable.
To prevent “fee sniping,” when Bitcoin Core creates transactions, it uses
nLocktime to
limit them to the “next block,” by default. In our scenario, Bitcoin Core
would set
nLocktime to 100,001 on any transaction it created. Under normal
circumstances,
this nLocktime has no effect—the transactions could only be included in
block
#100,001 anyway; it’s the next block.
But under a blockchain fork attack, the miners would not be able to pull
high-fee
transactions from the mempool, because all those transactions would be
timelocked
to block #100,001. They can only remine #100,000 with whatever
transactions were
valid at that time, essentially gaining no new fees.
To achieve this, Bitcoin Core sets the nLocktime on all new transactions
to <current
block # + 1> and sets the nSequence on all the inputs to 0xFFFFFFFE to
enable nLock
time.
Scripts with Flow Control (Conditional Clauses)
One of the more powerful features of Bitcoin Script is flow control, also
known as
conditional clauses. You are probably familiar with flow control in
various program‐
ming languages that use the construct IF...THEN...ELSE. Bitcoin
conditional clauses look
a bit different, but are essentially the same construct.
At a basic level, bitcoin conditional opcodes allow us to construct a
redeem script that
has two ways of being unlocked, depending on a TRUE/FALSE outcome of
evaluating a
logical condition. For example, if x is TRUE, the redeem script is A and
the ELSE
redeem script is B.
Additionally, bitcoin conditional expressions can be “nested”
indefinitely, meaning
that a conditional clause can contain another within it, which contains
another, etc.
Bitcoin Script flow control can be used to construct very complex scripts
with hun‐
dreds or even thousands of possible execution paths. There is no limit to
nesting, but
consensus rules impose a limit on the maximum size, in bytes, of a script.
Bitcoin implements flow control using the IF, ELSE, ENDIF, and NOTIF
opcodes. Addi‐
tionally, conditional expressions can contain boolean operators such as
BOOLAND,
BOOLOR, and NOT.
164
|
Chapter 7: Advanced Transactions and Scripting
At first glance, you may find the bitcoin’s flow control scripts
confusing. That is
because Bitcoin Script is a stack language. The same way that 1 + 1 looks
“backward”
when expressed as 1 1 ADD, flow control clauses in bitcoin also look
“backward.”
In most traditional (procedural) programming languages, flow control looks
like this:
if (condition):
code to run when condition is true
else:
code to run when condition is false
code to run in either case
In a stack-based language like Bitcoin Script, the logical condition comes
before the
IF, which makes it look “backward,” like this:
condition
IF
code to run when condition is true
ELSE
code to run when condition is false
ENDIF
code to run in either case
When reading Bitcoin Script, remember that the condition being evaluated
comes
before the IF opcode.
Conditional Clauses with VERIFY Opcodes
Another form of conditional in Bitcoin Script is any opcode that ends in
VERIFY. The
VERIFY suffix means that if the condition evaluated is not TRUE, execution
of the
script terminates immediately and the transaction is deemed invalid.
Unlike an IF clause, which offers alternative execution paths, the VERIFY
suffix acts as
a guard clause, continuing only if a precondition is met.
For example, the following script requires Bob’s signature and a pre-image
(secret)
that produces a specific hash. Both conditions must be satisfied to
unlock:
HASH160 <expected hash> EQUALVERIFY <Bob's Pubkey> CHECKSIG
To redeem this, Bob must construct an unlocking script that presents a
valid pre-
image and a signature:
<Bob's Sig> <hash pre-image>
Without presenting the pre-image, Bob can’t get to the part of the script
that checks
for his signature.
This script can be written with an IF instead:
HASH160 <expected hash> EQUAL
IF
Scripts with Flow Control (Conditional Clauses)
|
165
<Bob's Pubkey> CHECKSIG
ENDIF
Bob’s unlocking script is identical:
<Bob's Sig> <hash pre-image>
The script with IF does the same thing as using an opcode with a VERIFY
suffix; they
both operate as guard clauses. However, the VERIFY construction is more
efficient,
using one fewer opcode.
So, when do we use VERIFY and when do we use IF? If all we are trying to
do is to
attach a precondition (guard clause), then VERIFY is better. If, however,
we want to
have more than one execution path (flow control), then we need an
IF...ELSE flow
control clause.
An opcode such as EQUAL will push the result (TRUE/FALSE) onto
the stack, leaving it there for evaluation by subsequent opcodes. In
contrast, the opcode EQUALVERIFY suffix does not leave anything on
the stack. Opcodes that end in VERIFY do not leave the result on the
stack.
Using Flow Control in Scripts
A very common use for flow control in Bitcoin Script is to construct a
redeem script
that offers multiple execution paths, each a different way of redeeming
the UTXO.
Let’s look at a simple example, where we have two signers, Alice and Bob,
and either
one is able to redeem. With multisig, this would be expressed as a 1-of-2
multisig
script. For the sake of demonstration, we will do the same thing with an
IF clause:
IF
<Alice's Pubkey> CHECKSIG
ELSE
<Bob's Pubkey> CHECKSIG
ENDIF
Looking at this redeem script, you may be wondering: “Where is the
condition?
There is nothing preceding the IF clause!”
The condition is not part of the redeem script. Instead, the condition
will be offered
in the unlocking script, allowing Alice and Bob to “choose” which
execution path they
want.
Alice redeems this with the unlocking script:
<Alice's Sig> 1
The 1 at the end serves as the condition (TRUE) that will make the IF
clause execute
the first redemption path for which Alice has a signature.
166
|
Chapter 7: Advanced Transactions and Scripting
For Bob to redeem this, he would have to choose the second execution path
by giving
a FALSE value to the IF clause:
<Bob's Sig> 0
Bob’s unlocking script puts a 0 on the stack, causing the IF clause to
execute the sec‐
ond (ELSE) script, which requires Bob’s signature.
Since IF clauses can be nested, we can create a “maze” of execution paths.
The
unlocking script can provide a “map” selecting which execution path is
actually exe‐
cuted:
IF
script A
ELSE
IF
scriptELSE
scriptENDIF
ENDIF
B
C
In this scenario, there are three execution paths (script A , script B ,
and script C).
The unlocking script provides a path in the form of a sequence of TRUE or
FALSE val‐
ues. To select path script B, for example, the unlocking script must end
in 1 0
(TRUE, FALSE). These values will be pushed onto the stack, so that the
second value
(FALSE) ends up at the top of the stack. The outer IF clause pops the
FALSE value and
executes the first ELSE clause. Then the TRUE value moves to the top of
the stack and
is evaluated by the inner (nested) IF, selecting the B execution path.
Using this construct, we can build redeem scripts with tens or hundreds of
execution
paths, each offering a different way to redeem the UTXO. To spend, we
construct an
unlocking script that navigates the execution path by putting the
appropriate TRUE
and FALSE values on the stack at each flow control point.
Complex Script Example
In this section we combine many of the concepts from this chapter into a
single
example.
Our example uses the story of Mohammed, the company owner in Dubai who is
operating an import/export business.
In this example, Mohammed wishes to construct a company capital account
with
flexible rules. The scheme he creates requires different levels of
authorization depend‐
ing on timelocks. The participants in the multisig scheme are Mohammed,
his two
partners Saeed and Zaira, and their company lawyer Abdul. The three
partners make
decisions based on a majority rule, so two of the three must agree.
However, in the
Complex Script Example
|
167
case of a problem with their keys, they want their lawyer to be able to
recover the
funds with one of the three partner signatures. Finally, if all partners
are unavailable
or incapacitated for a while, they want the lawyer to be able to manage
the account
directly.
Here’s the script that Mohammed designs to achieve this:
IF
IF
2
ELSE
<30 days> CHECKSEQUENCEVERIFY DROP
<Abdul the Lawyer's Pubkey> CHECKSIGVERIFY
1
ENDIF
<Mohammed's Pubkey> <Saeed's Pubkey> <Zaira's Pubkey> 3
CHECKMULTISIG
ELSE
<90 days> CHECKSEQUENCEVERIFY DROP
<Abdul the Lawyer's Pubkey> CHECKSIG
ENDIF
Mohammed’s script implements three execution paths using nested IF...ELSE
flow
control clauses.
In the first execution path, this script operates as a simple 2-of-3
multisig with the
three partners. This execution path consists of lines 3 and 9. Line 3 sets
the quorum
of the multisig to 2 (2-of-3). This execution path can be selected by
putting TRUE
TRUE at the end of the unlocking script:
0 <Mohammed's Sig> <Zaira's Sig> TRUE TRUE
The 0 at the beginning of this unlocking script is because of a bug
in CHECKMULTISIG that pops an extra value from the stack. The
extra value is disregarded by the CHECKMULTISIG, but it must be
present or the script fails. Pushing 0 (customarily) is a workaround
to the bug, as described in “A bug in CHECKMULTISIG execution”
on page 150.
The second execution path can only be used after 30 days have elapsed from
the cre‐
ation of the UTXO. At that time, it requires the signature of Abdul the
lawyer and one
of the three partners (a 1-of-3 multisig). This is achieved by line 7,
which sets the
quorum for the multisig to 1. To select this execution path, the unlocking
script
would end in FALSE TRUE:
0 <Saeed's Sig> <Abdul's Sig> FALSE TRUE
168
|
Chapter 7: Advanced Transactions and Scripting
Why FALSE TRUE? Isn’t that backward? Because the two values are
pushed on to the stack, with FALSE pushed first, then TRUE pushed
second. TRUE is therefore popped first by the first IF opcode.
Finally, the third execution path allows Abdul the lawyer to spend the
funds alone,
but only after 90 days. To select this execution path, the unlocking
script has to end in
FALSE:
<Abdul's Sig> FALSE
Try running the script on paper to see how it behaves on the stack.
A few more things to consider when reading this example. See if you can
find the
answers:
• Why can’t the lawyer redeem the third execution path at any time by
selecting it
with FALSE on the unlocking script?
• How many execution paths can be used 5, 35, and 105 days, respectively,
after the
UTXO is mined?
• Are the funds lost if the lawyer loses his key? Does your answer change
if 91 days
have elapsed?
• How do the partners “reset” the clock every 29 or 89 days to prevent the
lawyer
from accessing the funds?
• Why do some CHECKSIG opcodes in this script have the VERIFY suffix while
others
don’t?
Bitcoin структуровано як мережу peer-to-peer зверху інтернету. Термін peer-to-peer, або P2P, означає, що комп'ютери, що приймають участь в мережі є сторонами один до одного, що вони всі рівні, що немає “особливих” вузлів, та що всі вузли розділяють тягар по запровадженню мережевих сервісів. Вузли мережі взаємодіють в решітчастій мережі з “пласкою” топологією. Немає сервера, немає централізованого сервісу, та немає ієрархії в мережі. Вузли в P2P мережі провадять та споживають послуги одночасно, на взаємних засадаї діючи як стимул для участі. Мережі P2P є природно стійкими, децентралізованими, та відкритими. Видатним прикладом архитектури P2P мережі був самий ранішній інтернет, коли вузли IP мережі були рівними. Сьогоднішня архитектура інтернет є більш ієрархічною, але протокол інтернета все ще зберігає свою пласко-рівневу основу.
За межами біткоіна, найширше та найбільш успішне застосування P2P технологій є розділення файлів, де Napster був піонером, та BitTorrent став найпізнішою еволюцією архитектури.
Мережева архитектура P2P Bitcoin є більше ніж вибір архитектури. Bitcoin є цифровою монетарною системою P2P по задумці, та мережева архітектура обоє, є відображення та основа цієї базової характеристики. Децентралізація керування є базовим принципом, що може бути досягнуто та підтримано пласкою, децентралізованою P2P мережею консенсуса.
Термін “мережа біткоін” посилається на набір вузлів, що виконують P2P
протокол біткоіна. На додаток до протокола біткоін P2P, існують також і
інші протоколи, такі як Stratum, що використовуються для майнингу, та
легковажних або мобільних гаманців. Ці додаткові протоколи провадяться
через сервери маршрутизації, що отримують до мережі біткоін, з
використанням протоколу біткоін P2P, та потім розширюють цю мережу
вузлами, що виконують інші протоколи. Наприклад, сервери Stratum поєднують
сервери майнінгу Stratum через протокол Stratum до головної мережі
біткоін, та перекидають протокол Stratum до протоколу біткоін P2P. Ми
використовуємо термін “розширена мережа біткоін” для посилання загальної
мережі, що включає протокол біткоіна P2P, протоколи майнінгових пулів,
протокол Stratum, та любі інші пов'язані протоколи, що поєднують
компоненти системи біткоін.
Хоча вузли в мережі біткоін P2P є рівними, вони можуть приймати на себе різні мови, в залежності від підтримуваної функціональності. Вузол біткоін є набором функцій: маршрутизація, база даних блокчейну, майнинг та послуги гаманця. Повний вузол з усіма ціма чотирма функціями, показаний на Малюнку 8-1.
Малюнок 8-1. Вузол мережі біткоін з усіма чотирма функціями: гаманець,
майнер, повна база даних блокчена, та мережева маршрутизація
Всі вузли включають функцію маршрутизації, щоб брати участь в мережі, та
можуть включати іншу функціональність. Всі вузли перевіряють та просувають
транзакції та блоки, та знаходять і підтримують з'єднання до інших сторін.
В прикладі повного вузла на Малюнку 8-1, функція маршрутизації позначена
помаранчевим колом з надписом “Вузол мережевої маршрутизації” або літерою
“N.”
Деякі вузли, що називаються повними вузлами, також підтримують повну та актуальну копію блокчейну. Повні вузли можуть автономно та авторитетно веріфікувати любу транзакцію без зовнішніх посилань. Деякі вузли обслуговують тільки підмножину блокчейну, та веріфікують транзакції, використовуючи метод, що називається спрощеною верифікацією платежів, або SPV. Ці вузли відомі як SPV вузли або легковажні вузли. В прикладі повного вузла на малюнку, функція зберігання повної бази даних блокчейну позначена синім колом з написом “Повний блокчейн”, або літерою “B.” На Малюнку 8-3, вузли SPV намальовані без синього кола, показуючи, що вони не мають повної копії блокчейна.
Майнаючі вузли змагаються за створення нових блоків через використання спеціалізованого обладнання для вирішення алгоритма доказу виконаної роботи. Деякі майнаючі вузли також є повними вузлами, що обслуговують повну копію блокчейну, тоді коли інші є легковажними вузлами, що беруть участь в майнінгових пулах, та покладаються на сервер пула для підтримки повного вузла. Функція майнінгу показана на повному вузлі як корне коло з надписом “Майнер” або літерою “M.”
Користувацькі гаманці можуть бути частиною повного вузла, як це загалом є для десктопних клієнтів біткоін. Все більше користувацьких гаманців, особливо що виконуються на ообмежених в ресурсах пристроях, як спартфони, є SPV вузлами. Функція гаманця показана на Малюнку 8-1 як зелене коло з надписом “Гаманець”, або літерою “W.”
На додаток до головних типів вузлів на протоколі біткоіна P2P, існують сервери та вузли, що виконують інші протоколи, такі, як спеціалізовані протоколи протоколи майнінгових пулів, та легковажні протоколи доступу клієнтів. Малюнок 8-2 показує найбільш загальні типи вузлів для розширеної мережі біткоін.
Головна мережа біткоін, що виконує протокол біткоін P2P, складаєтсья з від 5000 до 8000 слухаючих вузлів, що виконують різні версії референсного клієнта біткоін (Bitcoin Core), та декілька сотен вузлів, що виконують інші реалізації біткоін протоколу P2P, таких як Bitcoin Classic, Bitcoin Unlimited, BitcoinJ, Lib‐bitcoin, btcd, та bcoin. Неувеликий відсоток вузлів мережі біткоін P2P також є майнуючими вузлами, що змагаються в процесі майнингу, валідують транзакції, та створюю нові блоки. Різні великі компанії взаємодіють з мережею біткоін через виконання повних клієнтів на базі клієнта Bitcoin Core, з повною копією блокчейна та мережевого вузла, але без майнингу та функцій гаманця. Ці вузли діють як прикордонні мережеві маршрутизатори, дозволяючи різноманітні послуги (обмін, гаманці, дослідження блоків, обробку торгових платежів), що будуються зверху.
Розширена мережа біткоін включає мережу, що виконує мережевий протокол P2P. описаний вище, так само, як і вузли, що виконують спеціалізовані протоколи. Приєднані до головної мережі біткоін P2P network є декілька серверів пулів, та протокольних шлюзів, що поєднують вузли, які використовують різні протоколи. Ці інші вузли здебільшого є вузли пулів майнінгу (дивіться Главу 10) та легковажні клієнті гаманців, що не несе повної копії блокчейну.
Малюнок 8-3 показує розширену меержу біткоін з різними типами вузлів, серверами-шлюзами, прикордонними маршрутизаторами, та клієнтами гаманців, ат різні протоколи, що вони використовують для з'єднання один до одного.
Малюнок 8-2. Різні типи вузлів на розширеній мережі біткоінМалюнок 8-3. Розширена мережа біткоін, що показує типи вузлів, шлюзи та протоколи
В той час, коли мережа біткоіна P2P прислуговується головним потребам
широкого різноманіття типів вузлів, він виявляє дуже високу затримку
мережі для спеціалізованих потреб вузлів майнінгу біткоіна. Майнери
Bitcoin заохочуються в швидкому змаганні для вирішення проблеми доказу
виконанної роботи, та розширення блокчейна (дивіться Главу 10). Під час
цього змагання, майнери біткоін мають мінімізувати час між просуванням
блока-переможця, та початком наступного раунду змагань. В майнінгу
мережева затримка напряму пов'язана з рівнем доходів.
Релейна мережа Bitcoin Relay Network є мережею, що намагається мінімізувати затримкау в передачі блоків між майнерами. Оригінальна Bitcoin Relay Network була створена одним з головних розробників Matt Corallo в 2015му році, щоб дозволити синхронізацію блоків між майнерами з дуже малою затримкою. Мережа складається з декількох спеціалізованих вузлів, розташованих на інфраструктурі Amazon Web Services по всьому світі, та призначених для поєднання більшості майнерів та майнінгових пулів.
Оригінальна мережа Bitcoin Relay Network була замінена в 2016му році з вступом в дію пришвидшеної системи Fast Internet Bitcoin Relay Engine або FIBRE, також створеною розробником Matt Corallo. FIBRE є основаною на UDP релейною мережою, що пересилає блоки в мережі з вузлів. FIBRE реалізує компактну оптимізацію блоків для подальшого зменшення числа переданих даних та мережевої затримки.
Інша релейна мережа (все ще в фазі пропозиції) є Falcon, базована на дослідженнях в Cornell University. Falcon використовує “підрізану маршрутизацію”, замість “зберегти та переслати”, щоб зменшити затримку через просування блоків по мірі надходження, скоріше, ніж очікувати отримки цілого блока.
Релейні мережі не є заміною для мережі біткоін P2P. Замість цього вони є надбудованими мережами, що провадять додаткові поєднання між вузлами з спеціальними потребами. Як автостради не є замінником сільських доріг, але скоріше скороченнями між двома точками з великим трафіком, ви все ще потребуєте малі дороги для виїзду на шосе.
Коли новий вузол розпочинає роботу, він має знайти інші вузли біткоіна в
мережі, щоб прийняти участь в обміні. Щоб розпочати процес, новий вузол
має визначити щонайменьше один існуючий вузол в мережі, та під'єднатись до
нього. Географічне розташування інших вузлів не має значення; топологія
мережі біткоін географічно невизначена. Таким чином, любі існуючі вузли
біткоін можуть бути обрані випадково.
Щоб під'єднатись до відомого вузла, вузли встановлюють TCP з'єднання, звичайно на порту 8333 (порт, загально відомий, як той, що використовується в біткоін), або альтернативний порт, якщо він запроваджений. Під час встановлення з'єднання вузол почне з “привітання” (дивіться Малюнок 8-4), передаючи повідомлення з версією, що містить базову ідентифікуючу інформацію, включаючи:
(Дивіться GitHub щодо приклада повідомлення версії мережі).
Повідомлення версії завжди є першим повідомленням, надісланим з кожного вузла до іншого, Локальна сторона, отримавши повідомлення версії, буде перевіряти надіслану віддаленим вузлом версію, та вирішить, чи віддалений вузол є сумісним. Якщо віддалений вузол є сумісним, локальний вузол прийме повідомлення версії, та встановить з'єднання, надіславши verack.
Як новий вузол знаходить інші? Перший метод є запит DNS, використовуючи декілька “DNS зернят”, що є DNS серверами, що провадять список IP адрес вузлів. Деякі з ціх DNS зерен провадять статичний список IP адрес стабільно слухаючих вузлів біткоін. Деякі з DNS зерен є власними реалізаціями BIND (Berkeley Internet Name Daemon), що повертає випадковий набір зі списку адрес вузлів біткоін, що зібрані краулером або довго працюючим вузлом. Клієнт Bitcoin Core містить імена п'яти різних DNS зерен. Різноманітність в належності та різноманітність в реалізації різних DNS зерен забезпечує високій рівень надійності для початкового процесу розкрутки. В клієнті Bitcoin Core опція для використання DNS зернят контролюється опцією-перемикачем -dnsseed (встановлений в 1 по замовчанню для використання DNS зерен).
Альтернативно, розпочинаючий роботу вузол, що нічого не знає по мережу, має отримати щонайменьше одну IP адресу одного вузла біткоін після чого він може встановити з'єднання через подальше дослідження. Можуть бути використаний аргумент командного рядка -seednode, щоб з'єднатись до одного вузла, тільки для запитів щодо інших вузлів, використовуючи його як зернятко. Після того, як початковий вузол-зерно використаний для початкового завантаження, клієнт відключається від нього, та використовує тільки но отримані сторони.
Малюнок 8-4. Початкове привітання між сторонами
Коли один або більше з'єднань встановлено, новий вузол буде надсилати
повідомлення addr, що містить його власну IP аддресу своїм сусідам. Сусіди
будуть, в свою чергу, перевсилати повідомлення addr до своїх сусідів,
переконуючись, що новий вузол стане гарно відомим та краще з'єднаним.
Додатково, тільки що під'єднаний вузол може надіслати getaddr до своїх
сусідів, запитуючи їх повернути список IP адреси інших сторін. Таким
чином, вузол може знайти сторони, з якими можна зв'язатись, та
прорекламувати своє існування в мережі для інших вузлів. Малюнок 8-5
показує протокол пошуку адрес.
Малюнок 8-5. Просування адрес та виявлення
Вузол має з'єднатись до декількох різних вузлів, щоб встановити різні
шляхи в мережі біткоін. Шляхи не надійні — вузли з'являються та
відходять — так що вузел має продовжувати виявляти нові вузли, по мірі
втрати старих з'єднань, так само, як і допомагати іншим, коли вони
розпочинають роботу. Для розкручування потрібне тільки одне з'єднання,
оскільки перший вузол може запропонувати початкові свідоцтва до відомих
сторін, та ті вузли можуть надати подальші адреси. Також не має потреби,
та є марнотратством мережевих ресурсів, під'єднуватись більше ніж до
декількох вузлів. Після розкручування вузол буде пам'ятати його найбільш
останні вдалі з'єднання з вузлами, так що якщо він буде перезавантажений,
він швидко перевстановить з'єднання з його минулою мережею сторін. Якщо не
один з його відомих сторін не відповідає на запити, вузол може використати
зерна знову для нового розкручування в мережі.
На вузлі, що виконує Bitcoin Core, ви можете перелічити його з'єднання за
допомоги команди getpeerinfo:
$ bitcoin-cli getpeerinfo
[
{
"addr" : "85.213.199.39:8333",
"services" : "00000001",
"lastsend" : 1405634126,
"lastrecv" : 1405634127,
"bytessent" : 23487651,
"bytesrecv" : 138679099,
"conntime" : 1405021768,
"pingtime" : 0.00000000,
"version" : 70002,
"subver" : "/Satoshi:0.9.2.1/",
},
{
"inbound" : false,
"startingheight" : 310131,
"banscore" : 0,
"syncnode" : true
"addr" : "58.23.244.20:8333",
"services" : "00000001",
"lastsend" : 1405634127,
"lastrecv" : 1405634124,
"bytessent" : 4460918,
"bytesrecv" : 8903575,
"conntime" : 1405559628,
"pingtime" : 0.00000000,
"version" : 70001,
"subver" : "/Satoshi:0.8.6/",
"inbound" : false,
"startingheight" : 311074,
"banscore" : 0,
"syncnode" : false
Щоб перекрити автоматиче керування сторонами, та щоб задати список IP адрес, користувачі можуть запровадити опцію -connect=<IPAddress>, та вказати одну або більше IP адрес. Якщо використовується ця опція, вузол буде тільки з'єднуватись до обраних IP адрес, замість визначати та обслуговувати з'єднання зі сторонами автоматично. Якщо по з'єднанню немає трафіка, вузли будуть періодично надсилати повідомлення для підтримки з'єднання. Якщо вузол не комунікує по з'єднанню більше 90 хвилин, вважається, що він відключений, та буде обраний інший. Таким чином, мережа динамічно підлаштовується до нестійких вузлів та мережевих проблем, та може органічно зростати та зменшуватись без жодного централізованого контролю.
Повні вузли є такі вузли, що обробляють повний блокчейн з усіма транзакціями. Більш точно, вони можливо повинні називатись “вузли з повним блокчейном”. В ранішні роки біткоіна всі вузли були повними вузлами, та на сьогодні клієнт Bitcoin Core є вузлом з повним блокчейном. Однак в останні два роки, з'явились нові форми клієнтів біткоін, що не керують повним блокчейном, але виконуються як легковажні клієнти. Ми розглянемо їх в наступному розділі.
Повні вузли блокчейну підтримують повну та актуальну копію блокчейна
біткоінів з усіма транзакціями, що вони незалежно будують та перевіряють,
починаючи з самого першого блоку (блоку створення), та будуючи аж до
останнього відомого блоку в мережі. Пвний вузол блокчейну може незалежно
та достовірно перевірити любу транзакцію без звертання або покладання на
любий інший вузол або джерело інформації. Повний вузол блокчейну
покладається на мережу для отримання оновлень щодо нових блоків або
транзакцій, які він потім верифікує та вставляє у власну копію блокчейна.
Виконання повного вузла блокчейна надає вам чистий досвід біткоін:
незалезжну верифікацію всіх транзакцій без потреби покладатись або
довіряти любій іншій системі. Легко сказати, чи ви виконуєте повний вузол,
оскільки це потребує більше ста гігабайт постійного сховища (дискового
протосру), щоб зберігати повний блокчейн. Якщо вам треба багато диску, та
це займає два або три дні для синхронізації з мережею, ви виконуєте повний
вузол. Це ціна за повну незалежність та свободу від центральної влади.
Існує декілька альтернативних реалізацій повного клієна блокчейна,
побудованих на на різних мовах програмування та системних архитектурах.
Однак найбільш загальна реалізація є референсний клієнт Bitcoin Core,
також відомий як клієнт
Satoshi. Більше ніж 75% вузлів мережі біткоін виконують різні версії
Bitcoin Core. Він ідентифікується як “Satoshi” в рядку суб-версії, що
надсилається в повідомленні версії, та показується командою getpeerinfo.
як ми бачили раніше; наприклад, /Satoshi:0.8.6/.
Перша річ, що буде робити повний вузол, як тільки він з'єднається з іншою стороною, він буде намагатись побудувати повний блокчейн. Якщо це новий вузол, він не має блокчейну зовсім, він знає тільки один блок, блок творіння, що статично вбудований в клієнтське програмне забезпечення. Починаючи з блоку #0 (блок творення), новий вузол буде мати завантажити тисячі блоків для синхронізації з мережею, та відтворення повного блокчейну.
Процес синхронізації блокчейну починається з повідомлення версії,
оскільки воно містить BestHeight, поточну висоту блокчейна (кількість
блоків). Вузол буде дивитись на повідомлення версії від сторін, знати,
скільки блоків має кожний з них, та бути в змозі порівняти з тим, скільки
блоків він має в своєму блокчейні. Вузли сторін будуть отмінюватись
повідомленням getblocks, що містить хеш (відтиск) верхнього блоку їхнього
локального блокчейну. Один з вузлів буде в змозі ідентифікувати отримаинй
хеш, як той, що не належить блоку нагорі, але скоріше належить старішому
блоку, з чого роблячи висновок, що його блокчейн довший, ніж його візаві.
Сторона, що має довший блокчейн, та має більше блоків, ніж інший вузол,
може визначити, які блоки потребує інший вузол, та має завантажити сотні
тисячів блоків для синхронізації з мережою та відтворення повного
блокчейну. Він визначить перші 500 блоків для передачі, та передасть їх
хеші з використанням повідомлення inv (inventory). Вузол, якому не
вистачає ціх блоків, потім буде отримувати їх, через віддачу повідомлень
getdata, запитуючи повний блок даних, та ідентифікуючи запитані блоки з
використанням хешів з повідомлення inv.
Давайте уявімо, наприклад, що вузол має тільки блок творіння. Потім він отримає повідомлення inv від своїх співрозмовників, що міститиме хеші для наступних 500 блоків в ланцюгу. Він почне запитувати блоки в усіх підключених сторін, розподіляючи навантаження, та переконуючись, що він не перевантажує жодний з вузлів запитами. Вузол відстежує, як багато блоків є “в дорозі” на кожне з'єднання, означаючи блоки, що були запрошені, але ще не отримані, перевіряючи, що це число не перевищує обмеження (MAX_BLOCKS_IN_TRANSIT_PER_PEER). В такий спосіб, якщо йому потрібно багато блоків, він буде запитувати тільки нові, та не перевантажувати мережу. По мірі отримання кожного блоку, він додається до блокчейну, як ми побачимо в Главі 9. По мірі того, як локальний блокчейн відбудовується, більше блоків запитується та отримується, та процес продовжується, доки вузол не наздожене всю іншу мережу.
Цей процес порівняння локального блокчейну з вузлами, та отримання
недістаючих блоків, трапляється тільки під час того, як блок знаходиться
офлайн деякий період часу. В той час, коли вузол знаходився офлайн, та
пропустив декілька блоків, або цілий місяць, та пропустив декілька тисяч,
він починає з надсилання getblocks, отримує відповідь inv, та починає
завантажувати відсутні блоки. Малюнок 8-6 показує протокол інвентарізації
та просування блоків.
Малюнок 8-6. Синхронізація блокчейну вузлів через отримання блоків від
сторін
Не всі вузли мають можливість зберігати повний блокчейн. Багато Багато клієнтів біткоін розроблені щоб виконуватись в простір- та потужність-обмежених пристроях, таких, як спартфони, планшети, або вбудовані системи. Для таких пристроїв використовується метод спрощеної верифікації платежів (SPV), що дозволяє їм оперувати без зберігання повного блокчейну. Ці типи клієнтів назіваються SPV клієнтами, або легковажними клієнтами. По мірі зростання сприфняття біткоіну, вузли SPV стають найбільш загальною формою вузлів біткоін, особливо для гаманців біткоін.
Вузли SPV завантажують тільки заголовки блоків, та не завантажують транзакції, включені в кожний блок. Отриманий ланціг блоків, без транзакцій, в 1,000 разів меньший, ніж повний блокчейн. SPV вузли не можуть побудувати повну картину всіх UTXO, що доступні для витрачання, бо вони не знають щодо всіх транзакцій в мережі. SPV вузли перевіряють трензакції, використовуючи дещо іншу методологію, що покладається на сторони для отримання часткових розрізів маючих відношення частин блокчейна на вимогу. Як аналогія, повний вузол подібний до туриста в чужому місці, що оснащений детальною картою кожної вулиці та кожної адреси. Для порівняння, SPV вузол подубний до туриста в чужому місці, що питається випадкових перехожих, де повернути в певному напрямку, знаючи лише про головний бульвар. Хоча обоє туристи можуть перевірити наявність вулиці, навідавшись до неї, турист без мапи не знає, що розташоване в кінці кожної вулиці, та навіть не знає, що існують інші вулиці. Розташований перед домом на вулиці Будівельників 10, турист без мапи не може знати, чи є ще інші адреси Будівельників 10 в місці, та чи є ця адреса вірною. Турист без мапи в кращому випадку запитає досить людей, та сподіватись, які з них не намагаються пошуткувати з ним.
SPV пеервіряє транзакції за посиланням до їх глибини в блокчейні, замість їх висоти. В той час, коли повний вузол блокчейну буде будувати повний перевірений ланцюг з тісячів блоків, та транзакції досягають низу блокчейну (назад в часі) до самого блоку творіння, вузли SPV будуть перевіряти ланцюг з усіх блоків (але не всі транзакції), та пов'язувати цей ланцюг з транзакцією, що нас цікавить. Наприклад, при дослідженні транзакцій в блоці 300,000, повний вузол пов'язує всі 300,000 блоків донизу до блока творення, та будує повну базу UTXO, встановлюючи валідність транзакції через те, що UTXO залишились невитраченими.
Вузол SPV не може перевірити, що UTXO не витрачене. Замість цього вузол SPV буде встановлювати зв'язок між транзакцією та блоком, що містить її, використовуючи шлях Меркля (дивіться "Дерева Меркля"). Потім SPV вузол очікує, доки він не побачить шість блоків, від 300,001 до 300,006, накладені звурху блока, що містить транзакцію, та перевіряє її, встановлюючи її глибину під блоками від 300,006 до 300,001. Факт, що інші вузли мережі сприйняли блок 300,000, та потім виконали потрібну роботу для продукування ще шости блоків зверху для його підтвердження, та одночасно що транзакція не була двічі витрачена.
SPV вузол не може бути переконаний, що транзакція існує в блоці, коли
транзакція насправді не існує. Вузол SPV встановлює присутність транзакції
в блоці, запитуючи підтвердження шляху Меркля, та через валідацію
підтвордження виконаної роботи в ланцюзі блоків. Однак присутність
транзакції може бути “прихована” від SPV вузла. Вузол SPV однозначно може
впевнитись, що транзакція існує, але не може перевірити, що транзакція,
така, як повторне витрачення того самого UTXO, не існує, оскільки він не
має запису всіх транзакцій. Ця вразливість може біти використана в атаці
типа відмови в обслуговувані, або для атак подвійного витрачання проти
вузлів SPV. Щоб захиститись від цього, вузол SPV має випадково
підключатись до декількох вузлів, щоб підвищити вірогідність, що він має
з'язок з щонайменьше одним чесним вузлом. Ця потреба в випадкових зв'язках
означає, що вузли SPV також вразливі до атак розділення мережі, або атак
Sybil (захаращення мережі псевдонімами, найбільше відома через атаку
на Tor. прим. перекл.), коли вони під'єднуються до файкових вузлів,
або фейкових мереж, та на мають доступа до реальної мережі біткоін.
З більш практичних міркувань, гарно поєднані вузли SPV є досить безпечними, утримуючи баланс між потребами в русурсах, практичністю та безпекою. Однак для непохитної безпеки ніщо не зрівняється з повним вузлом блокчена. Повний вузол блокчейна перевіряє транзакцію через перевірку всього ланцюга з тисяч блоків пді нею, щоб гарантувати, що UTXO не витрачений, тоді як вузол SPV перевіряє, як глибоко блок похований під блоками нам ним.
Щоб отримати заголовки блоків, вузли SPV використовують повідомлення getheaders, замість getblocks. Відповідаюча сторона буде надсилати до 2,000 заголовків блоків, використовуючи одне повідомлення headers. В іншому процес той же самий, що і використовується повними вузлами для отримання повних блоків. Вузли SPV також встановлюють фільтр на з'єднання зі сторонами, щоб фільтрувати потік майбутніх блоків та транзакцій, надісланих сторонами. Любі цікаві транзакції отримуються з використанням запиту getdata. Сторона генерує повідомлення tx, що містить транзакції, в якості відповіді. Малюнок 8-7 показує синхронізацію заголовків блоків. Оскільки вузли SPV потребують отримувати специфічні транзакції, щоб вибірково перевіряти їх, вони також створюють ризик для приватності. На відміну від повних вузлів блокчейна, що збирають всі транзакції в кожному блоці, запити вузлів SPV щодо специфічних даних можуть ненавмисно виказати адресу в вашому гаманці. Наприклад, третя сторона, що моніторить мережу, може відстежити всі транзакції, запитані гаманцем вузла SPV, та використати це для асоціації адрес біткоіна з користувачем цього гаманці, зруйнувавши приватність користувача.
Малюнок 8-7. Вузол SPV синхронізує аголовки блоків
Швидко після появи SPV/легковажних вузлів, розробники біткоін додали можливість, що називається фільтрами Блума, щоб адресувати ризики приватності SPV вузлів. Фільтри Блума дозволяють SPV вузлам отримувати підмножину транзакцій, без розкриття, які саме адреси нас цікавлять, через механізм фільтрування, що використовує вірогідності, замість фіксованих шаблонів.
Фільтри Блума (або блумівські фільтри) є вірогіднісні фільтри пошуку, спосіб описати бажаний шаблон без його явного задання. Фільтри Блума пропонують ефективний шлях виражати шаблон пошуку, при цьому захищаючи приватність. Вони використовуються SPV вузлами для опитування своїх співрозмовників в пошуках транзакцій, відповідаючих специічним шаблонам, без розкриття, які саме адреси, ключі або транзакції ми шукаємо.
В нашій попередній аналогії, турист без мапи питає щодо певної адреси, Будівельників 10. Якщо він питає перехожих щодо напрямку до цієї вулиці, раніше чи пізніше він знайде напрямок. Блумівській фільтр схожий на запит "Чи є якісь вулиці пооблизу, чиї назви закінчуються на Н-К-В?". Запитання, як це, користувач розкриває трохи меньше щодо потрібного напрямку, ніж запитувати Будівельників 10. Використовуючи цей прийом, турист може вказати потірбну адресу в більших деталях, як “завершується на Л-Н-К-В”, або меньше деталей, як “завершується на В”. Через зміну точності пошуку, турист розкриває більше або меньше інформації, ціною отримання більших або меньших результатів. Якщо він запитує менш специфічний шаблон, він отримає більше можливих адрес, та кращу приватність, але багато результатів не будуть мати відношення. Якщо буде запитаний більш специфічний шаблон, буде отримано меньше результатів та втрачено більше приватності.
Блумівські фільтри служать цій функції, що дозволяє вузлу SPV вказувати шаблон пошуку для транзакцій, що можуть бути налаштовані в напрямку точності або приватності. Більш специфічний блумівський фільтр продукує більш точні результати, але ціною розкриття, в яких шаблонах зацікавлений SPV вузол, і, таким чином, розкриваючи адреси, якими володіє гаманець користувача. Менш специфічний блумівській фільтр буде продукувати більше даних щодо транзакцій, багато не маючих відношення до вузла, але це дозволить вузлу підтримувати кращу приватність.
Блумівські фільтри реалізовані як масиви змінної довжини з N бінарних цифр (бітових полів), та змінного числа з M хеш функцій. Хеш функції розроблені так, щоб завжди продукувати на виході значення від 1 до N, відповідно до масиву бінарних цифр. Хеш функції генеруються детерміністично, так що любий вузол, що реалізує блумівській фільтр, буде завжди використовувати ті самі хеш функції, та отримувати той самий результат для однакових даних на вході. Обираючи різну довжину (N) блумівськіх фільтрів, та різне число (M) хеш функцій, блумівській фільтр може бути налаштований, змінюючи рівень точності, та, таким чином, приватності.
На Малюнку 8-8 ми використовуємо дуже малий масив з 16 біт, та встановлюємо три хеш функції, щоб продемонструвати, як робить блумівській фільтр.
Малюнок 8-8. Приклад спрощеного блумівського фільтра, з 16-бітним полем та трьома хеш функціями
Блумівській фільтр ініціалізується так, що масив біт є всі нулі. Щоб
додати шаблон до блумівського фільтра, шаблон хешується кожною хеш
функцією по черзі. Застосовуючи першу хеш функцію до вхідних даних дає
число від 1 до N.
Малюнок 8-10. Додаючи другий шаблон “B” до нашого спрощеного блумівського
фільтра
Щоб протестувати, чи шаблон є частиною блумівського фільтра, шаблон хешується кожною функцією, та отриманий бітовий шаблон перевіряється по бітовому масиву. Якщо всі біти, індексовані хеш функцією, встановлені в 1, тоді шаблон, можливо, записаний в блумівській функції. Оскільки біти можуть бути встановлені як результат перекриття багатьох шаблонів, відповідь не є певною, але скоріше вірогіднісна. В простих виразах, позитивне співпадіння блумівського фільтра є "Можливо, так".
Малюнок 8-11 є прикладом перевірки наявності шаблона “X” в простому блумівському фільтрі. Відповідні біти встановлені в 1, так що шаблоно можливо співпадає.
Малюнок 8-11. Перевірка наявності шаблона “X” в блумівському фільтрі.
Результат є вірогіднісним позитивним співпадінням, що означає "Можливо".
На відміну від цього, якщо шаблон перевіряється по блумівському фільтру, та один з бітів встановлений в 0, це напевно означає, що шаблон не записаний в блумівському фільтрі. Негативний результат не є вірогідністю, це визначеність. Простими словами, негативне співпадіння на блумівському фільтрі є "Напевне ні".
Малюнок 8-12 є прикладом тестування існування шаблона “Y” в простому блумівському фільтрі. Один з відповідних біт встановллений в 0, так що шаблон напевне не співпадає.
Малюнок 8-12. Тестування існування шаблону “Y” в блумівському фільтрі. Результатом є визначено негативне співпадіння, що означає "Напевне ні".
Блумівські фільтри використовуються для фільтрування транзакцій (та блоків, що містять їх), що вузол SPV отримує від сторін, відбираючи тільки транзакції, що цікавлять SPV вузол, без розкриття, в яких адресах або ключах вони зацікавлені. Вузол SPV буде ініуіалізувати блумівській фільтр як “пустий”; в цьому стані блумівській фільтр буде співпадати з любими шаблонами. Вузол SPV потім складатиме список всіх адрес, ключів та хешей, в яких він зацікавлений. Він робить це, через виділення хеша публічного ключа, та хеша скрипта та ID транзакцій з UTXO, що контролюються гаманцем. Після цього вузол SPV додає кожний з них до блумівського фільтра, так що блумівській фільтр буде “співпадати”, якщо ці шаблони представлені в транзакції, без розкриття самих шаблонів.
Потім вузол SPV надсилатиме повідомлення filterload до іншої сторони, що
містить блумівській фільтр, що треба використовувати в з'єднанні. На тій
стороні блумівські фільтри перевіряються для кожної входячої транзакції.
Повний вузол перевіряє декілька частин транзакції з блумівськім фільтром,
шукаючи співпадіння, включаючи:
• ID транзакції
• Компоненти даних з блокуючих скриптів кожного виходу транзакцій (кожний
ключ та хеш в скрипті)
• Кожний зі входів транзакції
• Кожний з компонентів даних сигнатури входящих (або скрипта
підтвердження)
Перевіряючи всі ці компоненти, блумівські фільтри можуть бути використані для порівняння хешів публічних ключів, скриптів, значень OP_RETURN, публічних ключів в сигнатурах, або любій майбутній компоненті смарт контракті або складному скрипті.
Після встановлення фільтру сторона буде перевіряти вихід кожної транзакції на блумівському фільтрі. Тільки транзакції, що співпадають з фільтром, надсилаються до вузла. У відповідь на повідомлення getdata від вузла, сторони будуть надсилати повідомлення merkleblock, що містить тільки заголовки блоків, для блоків, що співпадають з фільтром та мерклівськім шляхом (дивіться “Мерклівські дерева”) для кожної транзакції. Інша сторона після цього надсилатиме tx повідомлення, що міститиме транзакції, що співпадають з фільтром. По мірі того, як повний вузол надсилає транзакції до SPV вузла, вузол SPV відхиляє любі фальшиві співпадіння, та використовує потрібні транзакції для оновлення свого набору UTXO та баланс в гаманці. По мірі того, як він оновлює свій погляд на набір UTXO, він також модифікує блумівській фільтр, щоб співпадати з подальшими транзакціями, що посилаються на тільки що знайдені UTXO. Повний вузол використовує новий блумівській фільтр для перевірки нових транзакцій, та весь процес повторюється.
Налаштування вузла щодо блумівського фільтра може інтерактивно додавати шаблони до фільтра, надсилаючи повідомлення filteradd. Щоб очистити блумівській фільтр, вузол може надіслати повідомлення filterclear. Оскільки неможливо видалити шаблон з блумівського фільтра, вузол має очистити та встановити новий блумівській фільтр, якщо деякий шаблон більше не потрібний. Мережевий протокол та механізм фільтрування для SPV вузлів визначений в BIP-37 (Peer Services).
Вузли, що реалізують SPV, мають слабшу приватність, ніж повний вузол. Повний вузол отримує всі транзакції, і, таким чином, не розкриває інформацію щодо того, чи використовує він деяку адресу в своєму гаманці. SPV вузол отримує фільтрований список транзакцій, що мають відношення до адрес, що є в його гаманці. Як результат, він зменшує приватність власника. Блумівські фільтри є шляхом для зменьшення втрати приватності. Без них вузол SPV буде мати явний список адрес, в яких він зацікавлений, створюючи суттєву прогалину в приватності. Однак, навіть з блумівськіми фільтрами, супротивник, що мониторить трафік SPV клієнта або напряму під'єднаний до нього як вузол P2P мережі, може з часом зібрати досить інформації, щоб розпізнати адреси в гаманці SPV клієнта.
Більшість нових користувачів біткоін вважають, що мережеві комунікації вузла біткоін є зашифровані. Фактично, оригінальна реалізація біткоін комунікує повністю відкрито. Хоча це не головна турбота безпеки повних вузлів, це велика проблема для SPV вузлів. Шляхом підвищити приватність мережі біткоін P2P, існує два рішення для запровадження шифрування комунікацій: транспорт Tor та P2P аутентифікація та шифрування BIP-150/151.
Tor, що означає мережу The Onion Routing, є програмним проектом та мережею, що надає шифрування та енкапсуляцію даних, через випадкові мережеві шляхи, що пропонує анонімність, невідстежуваність та приватність. Bitcoin Core пропонує декілька опцій конфігурації, що дозволяють вам виконувати вузол біткоін, надсилаючи трафк через мережу Tor. На додаток, Bitcoin Core також може запропоеувати прихований Tor сервіс, дозволяючи іншим Tor вузлам з'єднуватись до вашого вузла напряму через Tor.
В Bitcoin Core версії 0.12, вузол буде надавати прихований Tor сервіс автоматично, якщо він буде здатний підключитись до локального Tor сервіса. Якщо ви маєте встановлений Tor, та процес Bitcoin Core виконується як користувач з адекватними правами для доступу до аутефіканційного кукі Tor, він буде робити автоматично. Використовуйте флаг debug для ввімкнення налаштування Bitcoin Core для Tor сервісу, ось так:
$ bitcoind --daemon --debug=tor
Ви маєте побачити “tor: ADD_ONION successful” в журналі, вказуючи, що Bitcoin Core додав прихований сервіс до Tor мережі. Ви можете знайти більше інструкцій по виконанню Bitcoin Core як прихованого сервісу Tor в документації Bitcoin Core (docs/tor.md), та різних інструкціях онлайн.
Дві пропозиції Bitcoin Improvement Proposals, BIP-150 та BIP-151, додають підтримку для P2P аутентифікації та шифруванняв мережі біткоін P2P. Ці два BIP визначають опціональні сервіси, що можуть бути надані через сумісні вузли біткоін. BIP-151 дозволяє домовлене шифрування для всіх комунікацій між двома вузлами, що підтримують BIP-151. BIP-150 пропонує опціональну аутентифікацію сторони, що дозволяє вузлам вутентифікувати один одного з використанням ECDSA та приватних ключів. BIP-150 потребує, щоб перед аутентифікацією два вузли встановили шифроване з'єднання через BIP-151.
Станом на січень 2017, BIP-150 та BIP-151 не реалізовані в Bitcoin Core. Однак ці дві пропозиції були реалізовані щонайменьше в одній альтернативній реалізації клієнта біткоін, bcoin.
BIP-150 та BIP-151 дозволяють користувачам виконувати клієнти SPV, що під'єднані до довірених повних вузлів, використовуючи шифрування та аутентифікацію, для захисту приватності SPV клієнта. На додаток, аутентифікація може використовуватись для створення мереж довірених вузлів біткоін, та запобігання атакам посередників. Нарешті, шифрування P2P, при широкому розгортанні, посилить стійкість біткоіна до аналізу трафіка та порушуючих приватність досліджень, особливо в тоталітарних країнах, де використання інтернету значно контролюється та мониториться. Стандарт визначений в BIP-150 (Peer Authentication) та BIP-151 (Peer-to-Peer Communication Encryption).
Майже кожний вузол в мережі біткоін підтримує тимчасовий список непідтверджених транзакцій, що називається пул в пам'яті, мемпул, або пул транзакцій. Вузли використовують цей пул для відсліджування транзакцій, що відомі для мережі, але доки не включені в блокчейн. Наприклад, вузол-гаманець використовує пул транзакцій для відстеження надходячих платежів до гаманця користувача, що були отримані мережею, але досі не підтверджені. По мірі того, як транзакції додаються та верифікуються, вони додаються до пула транзакцій, та розсилаються до сусідніх вузлів, щоб просувати їх в мережі. Деякі реалізації також підтримують окремий пул загублених транзакцій. Якщо входи транзакції посилаються не транзакцію, що досі не відома, така, як відсутній батько, загублена транзакція буде тимчасово зберігатись в пулі загублених, доки не з'явиться батьківська транзакція.
Коли транзакція додана до пулу транзакцій, пул загублених перевіряється
щодо жодних загублених транзакцій, що посилаються на вихід транзакції
(дитину). Любі співпадаючі загублені транзакції валідуються. Якщо вона
валідна, вона видаляється з пулу загублених, та додаються до пулу
транзакцій, замикаючи ланцюг, що почався з батьківської транзакції. В
світі нової доданої транзакції, що більше не загублена, процес
повторюється рекурсивно, шукаючи подальших нащадків, доки інших нащадків
не буде знайдено. На протязі цього процесу, надходження батьківської
транзакції перемикає каскад реконструкції цілого ланцюга незалежних
транзакцій, через поєднання загублених транзакцій з їхніми батьками, і так
далі по ланцюгу. Обоє, пул транзакцій та пул загублених (якщо
реалізований) зберігаються в локальній пам'яті, та не зберігаються в
постійному сховищі; скоріше, вони динамічно заповнюються з входящих
мережевих повідомлень. Коли вузол стартує, обоє пули пусті, та поступово
заповнюються новими транзакціями, отриманими з мережі.
Деякі реалізації клієнтів біткоін обслуговують базу даних або пул UTXO,
що є набором всіх невитрачених виходів блокчейну. Хоча ім'я “пул UTXO”
виглядає подібним до пулу транзакцій, він представляє інший набір даних.
На відміну від пулів транзакцій та загублених, пул UTXO не ініціалізується
пустим, та замість цього містить мільйони входжень невитрачених виходів
транзакцій, все що невитрачено за весь час з самого початку, до блоку
творення.Пул UTXO може розміщуватись в локальній пам'яті, або як
індексована база даних в постійному сховищі.
Хоча пули транзакцій та загублених представляють локальну перспективу
поодинокого вузла, та можуть значно варіюватись від вузла до вузла, в
залежності від того, коли вузол був стартований або рестартований, пул
UTXO представляє досягнутий консенсус мережі, і, таким чином, може
розрізнятись тільки незначно між вузлами. Більше того, пули транзакцій та
загублених містять тільки непідтверджені транзакції, тоді як пул UTXO
містить тільки підтверджені транзакції.
Структура даних блокчейну є впорядкований, зв'язаний список блоків з транзакцій. Блокчейн може зберігатись в пласкому файлі, або в простій базі даних. Клієнт Bitcoin Core зберігає метадані блокчейну, використовуючи базу даних Google LevelDB. Блоки пов'язані “назад”, кожний посилається на попередній блок в ланцюжку. Блокчейн часто візуалізується як вертикальний стек, де блоки накладають зверху один одного, та блок творення прислуговується основою стеку. Візуалізація блоків в вигляді накладених один на одний призводить до виникнення відповідних термінів, таких, як "висота", що посилається на відстань від першого блоку, та "гора" або "верхівка", що посилаються на самий останній доданий блок. Кожний блок в блокчейні ідентифікується хешем, згенерованим криптографічним хеш алгоритмом SHA256 на заголовці блока. Кожний блок також посилається на попередній блок, відомий як батьківській блок, через поле "хеш попереднього блока" в заголовці блока. Іншими словами, кожний блок містить хеш свого батька в своєму заголовку. Послідовність хешів поєднує кожний блок з батьківськім та створює ланцюг, що іде назад до першого будь-коли створеного блоку, відомого як блок творення. Хотя блок має тільки одного батька, він може тимчасово мати більше одного нащадка. Кожний з нащадків посилається на той самий блок як на предок, та містить той самий (батьківський) хеш в полі "хеш попереднього блоку". Декілька дітей з'являються під час "розгалуження" блокчейну, тимчасової ситуації, що виникає, коли різні блоки винайдені майже одночасно різними майнерами (дивіться “Розгалуження блокчейну”). З часом один з дочірніх блоків стає частиною блокчпйну, та "розгалуження" стає влагодженин. Навіть зважаючи, що блок може мати більше одного нащадка, кожний блок може мати лише одного предка. Це так, бо блок має лише одне поле "хеш попереднього блока", що посилається на одного предка.
Поле “хеш попереднього блока” розташоване в загаловці блока, і, таким чином, впливає на хеш поточного блоку. Власна ідентичність нащадка змінюється, якщо змінюється ідентичність батька. Якщо батько змінюється в деякий спосіб, змінюється і його хеш. Змінений хеш батька потребує зміну вказівника "хеш попереднього блоку" нащадка. Це, в свою чергу, викликає зміну хешу нащадка, та нащадка нащадка, і так далі. Цей каскадний ефект гарантує, що коли є багато поколінь після деякого блоку, він не може бути змінений без примусового переобчислення всіх послідовних блоків. Оскільки таке переобчислення може потребувати неможливих обчислень (і, таким чином, витрати енергії), наявність довгого ланцюга з блоків робить глибоку історію блокчена незмінною, що є ключовою властивістю безпеки біткоіна.
Одним зі шляхів думати про блокчейн, це як про шари в геологічній формації, або зразом моделі льодовика. Поверхневі шари можуть змінюватись кожної пори року, або навіть змиті, доки вони не матимуть часу відкластись. Але коли ви переходите на декілька дюймів далі, геологічні шари стають більше і більше стабільними. Під час, коли ви дивитесь на декілька сотен футів нижче, ви дивитесь на знімок минулого, що залишалось непотурбованим мільйони років. В блокчейні найбільш останні блоки можуть переглянуті, якщо відбудеться переобчислення ланцюга через розгалуження. Верхівка з шести блоків подібні на зовнішні шару грунуту. Але коли ви йдете глибше в блокчейн, блоки все меньше та меньше вірогідно змінені. Після 100 блоків назад, існує так багато стабільності, що транзакція коінбейс — транзакція, що містить новий відкарбований біткоін — може бути витрачений. Декілька тисяч блоків назад (місяць) блокчейн є сталою історією, для всіх практичних застосувань. Тоді як протокол завжди дозволяє відкатити ланцюг через довший ланцюг, та в той час, коли завжди існує можливість зміни кожного блоку, вірогідність такої події зменьшується з плином часу, доки не стане нескінчено малою.
Блок є контейнерною структурою даних, що агрегує транзакції для включення в публічний часопис, блокчейн. Блок складається з заголовка, що містить метадані, за яким слідує довхий список транзакцій, що складають основну долю. Блок заголовку має 80 байт, тоді як середня транзакція є щонайменьше 250 байтів, та середній блок містить більше ніж 500 транзакцій. Повний блок з усіма транзакціями є, таким чином, в 1000 разів довший, ніж заголовок блоку. Таблиця 9-1 описує структуру блоку.
Таблиця 9-1. Структура блоку
| Розмір |
Поле |
Опис |
| 4 байти | розмір блоку | Розмір блоку, в байтах, що іде за цім полем |
| 80 байтів | заголовок блоку | Декілька полів з заголовку блока |
| 1-9 байт | лічильник транзакцій | Кількість транзакцій в блоці |
| Варіант | транзакції | Транзакції, записані в блоці |
The block header consists of three sets of block metadata. First, there
is a reference to
a previous block hash, which connects this block to the previous block in
the block‐
chain. The second set of metadata, namely the difficulty, timestamp, and
nonce, relate
to the mining competition, as detailed in Chapter 10. The third piece of
metadata is
the merkle tree root, a data structure used to efficiently summarize all
the transac‐
tions in the block. Table 9-2 describes the structure of a block header.
Table 9-2. The structure of the block header
| Розмір | Поле | Опис |
| 4 байти | версія | Числовий номер для відстеження оновлень програми або протокола |
| 32 байти | хеш попереднього блока | Посилання на хеш попереднього (бітьківського) блока в ланцюгу |
| 32 байти | мерклівській корінь | Хеш кореня мерклівського дерева транзакцій цього блока |
| 4 байти | часовий відтиск | Приблизний час створення цього блока (секунди Юнікс-епохи) |
| 4 байти | цільова складність | Ціль складності алгоритма підтвордження виконаної роботи для цього блока |
| 4 байти | довісок | Лічильник, використаний в алгоритмі перевірки виконаної роботи |
Довісок, цільова складність та відтиск часу використовуються в процесі майнингу, та будуть обговорюватись більш детально в Главі 10.
Первинний ідентифікатора блоку є його криптографічний хеш, цифровий
відтиск, отриманих хешуванням заголовку блока двічи за допомогою алгоритма
SHA256. Отриманий 32-байтний хеш називається хешем блока, але точніше його
треба називати хешем заголовка блока, оскільки тільки заголовок блока
використовується для його обчислення. Наприклад,
000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f є хешем
блока першого створеного блоку біткоін. Хеш блоку ідентифікує блок
унікально та безсумнівно, та може бути незалежно виведений любим вузлом
простим хешуванням заголовка блока.
Зауважте, що хеш блоку насправді не включений в структуру даних блоку, ні коли блок передається по мережі, ні коли він зберігається в постійному сховищі вузла як частина блокчейну. Замість цього хеш блока обчислюється кожний раз, коли блок отримується з мережі. Хеш блока може бути збережений в окремій таблиці бази даних, як частина метаданих блоків, щоб спростити індексування та скоріше отримувати блоки з диску.
Другий блок ідентифікує блок по його позициї в блокчейні, що називається
висотою блока. Перший будь-коли створений блок має висоту блока 0 (нуль),
та той самий блок, що був попередньо посиланий наступним хешем блока
000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f. Блок
може, таким чином, бути ідентифікований в два способи: через посилання на
хеш блоку, або через посилання висоти блока. Кожний наступний блок додаєть
"нагору" цього першого блоку на одну позицію вище в блокчейні, як ящики,
поставлені один на одний. Висота блоків на 1 січня 2017 року був приблизно
446,000, що означає, що 446,000 блоків покладені зверху першого блока,
створеного в січні 2009. На відміну від хешу блока, висота блока не є
унікальним ідентифікатором. Хоча окремий блок завжди має специфічну та
незмінну висоту блока, зворотнє не є вірним — висота блока не завжди
ідентифікує окремий блок. Два або більше блоків можуть мати ту саму висоту
блока, змагаючись за ту саму позицію в блокчейні. Цей сценарій детально
обговорений в розділі “Розгалуження блокчейн”. Висота блока також не є
частиною структури даних блока; вона не збурігається в блоці. Кожний блок
динамічно ідентифікується свою позицію блока (висоту) в блокчейні, коли
він отримується з мережі біткоін. Висота блока може також зберігатись як
метадані в індексованій базі даних для швидшого отримання. Хеш блоку
завжди унікально індифікує блок. Блок також завжди має певну висоту блока.
Однак не завжди так, що висота блока ідентифікує окремий блок. Скоріше,
два або більше блоків можуть сперечатись за одну позицію в
блокчейні.
Перший блок в блокчейні називається блоком творення, та був створений в 2009му році. Він є загальним предком всіх блоків в блокчейні, що означає, що якщо ви почнете з любого блока, та прослідуюте назад в часі, ви з часом натрапите на блок творення.
Кожний вузол завжди починається щонайменьше з одного блока, оскільки блок творення статично закодований в програмі клієнта біткоін, так що він не може бути змінений. Кожний вузол завжди “знає” хеш та структуру блока творення, фіксований час його створення, та навіть одну транзакцію в ньому. Таким чином, кожний вузол має стартову точку для блокчейну, безапечний “корінь”. від якого можна будувати довірений блокчейн. Подивіться на статичний блок творення в клієнті Bitcoin Core, в файлі chainparams.cpp.
Наступний хеш ідентифікатор належить блоку творення:
000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f
Ви можете пошукати цей блок-хеш на любому сайті-переглядачі блока, такому, як blockchain.info, і в и знайдете сторінку, що описує вміст блоку, з URL, що містить хеш:
https://blockchain.info/block/000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f
https://blockexplorer.com/block/000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f
Використовуючи референсний клієнт Bitcoin Core з командного рядка:
$ bitcoin-cli getblock
000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f
{
"hash" : "000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f",
"confirmations" : 308321,
"size" : 285,
"height" : 0,
"version" : 1,
"merkleroot" : "4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b",
"tx" : [
"4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b"
],
"time" : 1231006505,
"nonce" : 2083236893,
"bits" : "1d00ffff",
"difficulty" : 1.00000000,
"nextblockhash" : "00000000839a8e6886ab5951d76f411475428afc90947ee320161bbf18eb6048"
}
Блок творіння містить приховане в собі повідомлення. Вхід транзакції коінбейс містить текст “The Times 03/Jan/2009 Chancellor on brink of second bailout for banks”. Це повідомлення було признечене для надання гарантіі щодо самої ранішньої дати, коли був створений цей блок, через посилання на заголовок британської газети The Times. Воно також служить як грайливе нагадування про важливість незалежної монетарної системи, і що біткоін почав своє існування в той самий час, коли розгортався безпрецендентний світовий монетарний кризис. Повідомлення було вбудоване в перший блок Satoshi Nakamoto, створювачем біткоін.
Повні вузли біткоіну обслуговують локальну копію блокчейну, починаючи з блоку творіння. Локальна копія блокчейну постійно оновлюється, по мірі знаходження нових блоків, та вони використовуються для поширення ланцюга. Коли вузол отримує входящі блоки з мережи, він перевіряє ці блоки, та потім зв'язує їх з існуючим блокчейном. Щоб встановити зв'язок, вузол буде перевіряти заголовок надійшовшого блоку, та дивитись на "хеш попереднього блоку".
Уявімо, наприклад, що вузол має 277,314 блоків в локальній копії блокчейну. Останній блок, про який знає вузол, є блок 277,314, з хешем заголовку: 00000000000000027e7ba6fe7bad39faf3b5a83daed765f05f7d1b71a1632249. Потім вузол біткоін отримує новий блок з мережі, який він розбирає наступним чином:
{
"size" : 43560,
"version" : 2,
"previousblockhash" : "00000000000000027e7ba6fe7bad39faf3b5a83daed765f05f7d1b71a1632249",
"merkleroot" : "5e049f4030e0ab2debb92378f53c0a6e09548aea083f3ab25e1d94ea1155e29d",
"time" : 1388185038,
"difficulty" : 1180923195.25802612,
"nonce" : 4215469401,
"tx" : [
"257e7497fb8bc68421eb2c7b699dbab234831600e7352f0d9e6522c7cf3f6c77",
#[... далі багато транзакцій пропущені ...]
}
]
"05cfd38f6ae6aa83674cc99e4d75a1458c165b7ab84725eda41d018a09176634"
Дивлячись на цей новий блок, вузол знаходить поле previousblockhash, що містить хеш попереднього блоку. Цей хеш відомий вузлу, та він належить останньому блоку в ланцюгу на висоті 277,314. Таким чином, новий блок є дитиною останнього блоку в ланцюгу, та розширює існуючий блокчейн. Вузол додає цей новий блок в кінець ланцюга, що робить блокчейн довшим, з новою довжиною 277,315. Малюнок 9-1 показує ланцюг з трьох блоків, пов'язаних через посилання в полі previousblockhash.
Кожний блок в блокчейні біткоін містить підсумок всіх транзакцій в
блоці, з використанням дерев Меркля. Мерклівське дерево, також відоме як
бінарне хеш дерево, є структурою даних, що використовуються для
ефективного підсумку та перевірки цілосності великих наборів даних.
Мерклівські дерева є бінарними деревами, що містять криптографічні хеші.
Термін "дерево" використовується в комп'ютерних науках, щоб описувати
розгалужені структуру даних, але ці дерева зазвичай зображують до гори
низом, з "коренем" зверху, та "листям" знизу діаграми, як ви бачита
в наступних прикладах.
Малюнок 9-1. Блоки, пов'язані в ланцюг через посилання на хеш заголовку попереднього блоку
Мерклівські дерева використовуються в біткоіні для підсумку всіх транзакцій в блоці, виробляючи загальний цифровий відтиск всього набору транзакцій, провадячи дуже ефективний процес для перевірки, чи транзакція включена в блок. Мерклівське дерево конструююється через рекурсивне хешування пар вузлів, доки не залишиться тільки один хеш, що називається коренем, або мерклівськім коренем. Криптографічний хеш алгоритм, що використовується в мерклівськіх деревах біткоін є SHA256, застосований двічі, також відомий як подвійний-SHA256.
Коли N елементів даних хешуються та підсумовуються в мерклівському
дереві, ви можете перевірити, та побачити, чи деякий елемент знаходиться в
дереві щанайбільше за 2*log2(N) обчислень, роблячи це дуже ефективною
структурою даних. Мерклівське дерево будується знизу догори. В наступному
прикладі ми починаємо з чотирьох транзакцій, A, B, C, та D, що формують
листя мерклівського дерева, як показно на Малюнку 9-2. Транзакції не
зберігаються в мерклівському дереві; скоріше, їх дані захешовані, та
отриманий хеш зберігається в кожному вузлі-листі, як HA, HB, HC, and
HD:
HA = SHA256(SHA256(Транзакція A))
Послідовні пари листяних вузлів потім підсумовуються в батьківському
вузлі, через конкатенацію двох хешів, та знову хешування отриманого рядка.
Наприклад, щоб сконструювати батьківській вузол H AB, два 32-байтні хеші
дітей конкатенуються, що створити 64-байтний рядок. Цей рядок потім двічі
хешується, щоб отримати хеш батьківського вузла: HAB = SHA256(SHA256(HA +
HB)). Процес продовжується, доки нагорі не залишиться лише один елемент,
вузол, відомий я мерклівській корінь. Цей 32-байтний хеш зберігається в
заголовку блока, та підсумовує всі дані в усіх транзакціях. Малюнок 9-2
показує, як корінь обчислюється через попарні хеші вузлів.
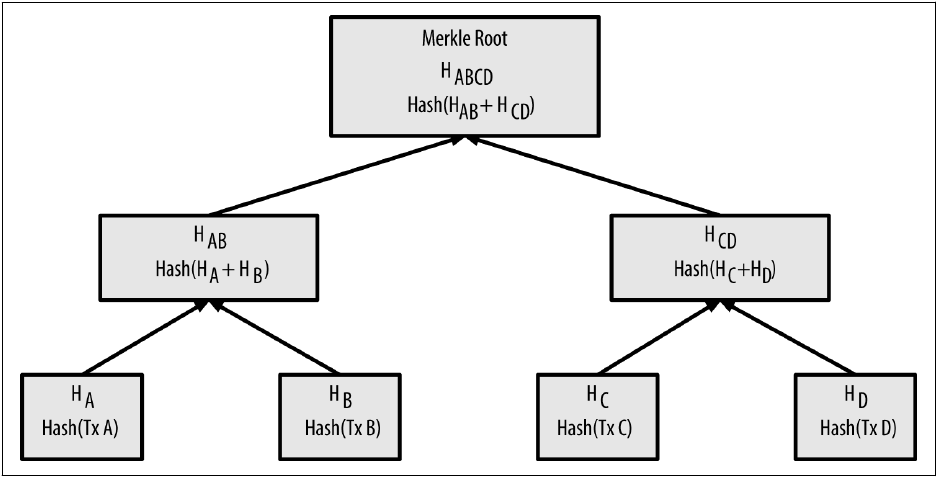
Малюнок 9-2. Обчислення вузлів в мерклівському дереві
Оскільки мерклівське дерево є бінарним деревом, йому потрібно мати парне число листів. Якщо треба підсумувати непарне число транзакцій, хеш останньої транзакції буде продубльовано, щоб створити парне число вузлів, що також відоме як збалансоване дерево. Це показано на Малюнку 9-3, де транзакція C продублікована.
Малюнок 9-3. Дублювання одного елементу даних дає парне число елементів даних
Той самий метод конструювання дерева з восьми транзакцій може бути узагальнений для конструюванню дерев любого розміру. В біткоіні є загальним мати від декількох сотен та більше тисячі транзакцій в одному блоці, що підсумоване в рівно той самий спосіб, продукуючи тільки 32 байтів даних, як єдиний мерклівській корінь. На Малюнку 9-4 ви бачите дерево, побудоване з 16 транзакцій. Зауважте, що хоча корінь виглядає більшим ніж вузли на диаграмі, він такого самого розміру, тільки 32 байтів. Чи є в нас одна транзакція, або чи є сотня тисяч транзакцій в блоці, мерклівській корінь завжди дає їх підсумок розміром 32 байти.
Щоб переконатись, що окрема транзакція включена в блок, вузлу треба
тількки спродукувати log2(N) 32-байтних хешів, відбудовуючи шлях
аутентифікації, або мерклівській шлях, що поєднує окремі транзакції до
кореня дерева. Це особливо важливо, коли число транзакцій зростає, бо
логарифм по сонові 2 від числа транзакцій зростає значно більш повільно.
Це дозволяє вузлам біткоін ефективно продукувати шляхи з 10 або 12 хешів
(320–384 байт), що може надати гарантію, що окрема транзакція є однією з
більше ніж тисячі транзакцій в блоці розміром мегабайт.
Малюнок 9-4. Мерклівське дерево підсумовує багато елементів даних
На Малюнку 9-5, вузол може переконатись, що транзакція K включена в блок,
через продукування маркліського шляху, що довжиною тільки чотири 32-байтні
хеші (128 байтів загалом). Шлях складається з чотирьох хешів (показаних з
зафарбованим фоном на Малюнку 9-5) HL, HIJ,
HMNOP, та HABCDEFGH. З ціма чотирма хешами, що провадять шлях
аутентифікації, кожний вузол може перевірити, що HK (з чорним фоном
знизу діаграми) включений в мерклівській корінь, через обчислення
додаткових попарних хешів HKL, HIJKL, HIJKLMNOP, та корінь мерклівсього
дерева (обведене приривчастою лінією на діаграмі).
Малюнок 9-5. марклівській шлях, що використовується для перевірки
входження елементу даних
Код в Прикладі 9-1 демонструє процес створення мерклівського дерева з
хешів вузлів-листя, далі нагору до кореня, з використанням бібліотеки
libbitcoin для деяких допоміжних функцій.
Приклад 9-1. Побудова мерклівського дерева
#include <bitcoin/bitcoin.hpp>
bc::hash_digest create_merkle(bc::hash_list& merkle)
{
// Припинити, якщо список хешів порожній.
if (merkle.empty()) return bc::null_hash;
else if (merkle.size() == 1) return merkle[0];
// Доки існує більше одного хешу в списку...
while (merkle.size() > 1) {
if (merkle.size() % 2 != 0) merkle.push_back(merkle.back()); // Дублікуємо останній хеш, якщо список непарний.
assert(merkle.size() % 2 == 0); // Тепер список парний. (неуявна ситуація, коли це б не мало тут бути. прим. перекл.)
bc::hash_list new_merkle; // Новий список хешів.
// Проходимо до два за раз.
for (auto it = merkle.begin(); it != merkle.end(); it += 2) {
bc::data_chunk concat_data(bc::hash_size * 2); // Конкатенуємо два хеші разом.
auto concat = bc::serializer<
decltype(concat_data.begin())>(concat_data.begin());
concat.write_hash(*it);
concat.write_hash(*(it + 1));
bc::hash_digest new_root = bc::bitcoin_hash(concat_data); // Хешуємо обоє хеши.
new_merkle.push_back(new_root); // Додаємо до нового списку.
}
merkle = new_merkle; // Це новий список.
}
// DEBUG output -------------------------------------
std::cout << "Поточний мерклівський хеш список:" << std::endl;
for (const auto& hash: merkle)
std::cout << " " << bc::encode_base16(hash) << std::endl;
std::cout << std::endl;
// --------------------------------------------------
}
// Нарешті повертаємо один елемент.
return merkle[0];
}
int main()
{
// Замініть ці хеші з блоку, щоб відтворити той самий мерклівській корінь.
bc::hash_list tx_hashes{{
bc::hash_lit
eral("0000000000000000000000000000000000000000000000000000000000000000"),
bc::hash_lit
eral("0000000000000000000000000000000000000000000000000000000000000011"),
bc::hash_lit
eral("0000000000000000000000000000000000000000000000000000000000000022"),
}};
const bc::hash_digest merkle_root = create_merkle(tx_hashes);
std::cout << "Result: " << bc::encode_base16(merkle_root) << std::endl;
return 0;
}
Приклад 9-2 показує результат компіляції та виконання мерклівського коду.
Example 9-2. Компіляція та виконання прикладу мерклівського коду
$ # Компілюємо код merkle.cpp
$ g++ -o merkle merkle.cpp $(pkg-config --cflags --libs libbitcoin)
$ # Виконуємо мерклівську програму
$ ./merkle
Current merkle hash list:
32650049a0418e4380db0af81788635d8b65424d397170b8499cdc28c4d27006
30861db96905c8dc8b99398ca1cd5bd5b84ac3264a4e1b3e65afa1bcee7540c4
Current merkle hash list:
d47780c084bad3830bcdaf6eace035e4c6cbf646d103795d22104fb105014ba3
Result: d47780c084bad3830bcdaf6eace035e4c6cbf646d103795d22104fb105014ba3
Ефективність мерклівських дерев стає очевидною по мірі маштабування.
Таблиця 9-3 показує обсяг дангих, що потрібен для обміну як мерклівський
шлях, щоб переконатись, що транзакція є частиною блока.
Таблиця 9-3. Ефективність мерклівського шляху
| Число транзакцій | Примірний розмір блоку | Розмір шляху (хешів) | Розмір шляху (байт) |
| 16 транзакцій | 4Кб | 4 хеші | 128 байт |
| 512 транзакцій | 128Кб | 9 хешів | 288 байт |
| 2048 транзакцій | 512Кб | 11 хешів | 352 байтів |
| 65535 транзакцій | 12Мб | 16 хешів | 512 байтів |
Мерклівські дерева активно використовуються вузлами SPV. Вузли SPV не мають всіх транзакцій, та не завантажують повні блоки, але тільки заголовки блоків. Щоб перевірити, що транзакція включена в блок, без того, щоб завантажувати всі транзакції в блоці, вони використовують шлях аутентифікації, або мерклівський шлях.
Розглянемо, наприклад, вузол SPV, що зацікавлений у вхідних платежах на адресу, що міститься в його гаманці. Вузол SPV буде встановлювати блумівській фільтр (дивіться "Блумівські фільтри") на своїх з'єднаннях до сторін, щоб обмежити отримані транзакції до тільки тих, що містять потрібну адресу. Коли сторона бачить транзакцію, що співпадає з блумівськім фільтром, вона надсилає цей блок з використанням повідомлення merkleblock. Повідомлення merkleblock містить заголовок блоку, так само, як і мерклівський шлях, що пов' язує цікаву транзакцію з мерклівським коренем блоку. Вузол SPV може використати цей мерклівській шлях для з'єднання транзакції з блоком, та перевірити, що транзакція включена в блок. Вузол SPV також використовує заголовок блоку для поєднання блоку з рештою блокчейну. Комбінація ціх двох посилань, між транзакцією та блоком, та між блоком та блокчейном, дає гарантію, що транзакція знаходиться в блокчейні. Врешті решт, вузол SPV має отримати меньше ніж кілобайт даних для заголовка блоку та мерклівського шляху, розмір даних, що більше ніж в тисячу разів меньше, ніж повний блок (наразі близько 1Мб).
Ви можете бути здивовані, коли пізнаєте, що існує більше одного блокчейну біткоін. "Головний" блокчейн біткоіна, той що створений Satoshi Nakamoto третього січня 2009го року, той самий що має блок творіння, про який ми казали в цій главі, ми називаємо mainnet. Існують інші блокчейни біткоіну, що використовуються для тестування: наразі це testnet, segnet, та regtest. Давайте поглянемо на кожний з них.
Testnet є назвою для тестового блокчейна, мережі та грошей, що використовуються для тестових цілей. Тестнет є повністю функціональню живою мережою P2P, з гаманцями, тестовими біткоінами (монетами тестнету), майнингом, та всіма іншими властивостями mainnet. Існує, насправді, тільки дві відмінності: монети тесткоіну призначені бути нічого не вартими, та складність майнінгу має бути досить низькою, щоб будь-хто міг майнати монети тестнету досить легко (залишаючи їх нічого не вартими).
Люба розробка програмного забезпечення, що призначене для виробничого застосування в бітнет mainnet, повинна з початку бути протестована на testnet за допомогою тестових монет. Це захисстить обоє, і розробника від монетарних втрат через помилки, та мережу від несподіваної поведінки через помилки.
Утримання монет не вартими нічого, та легкий майнинг, однак, не є простим. Не зважаючи на зауваження розробників, деякі люди використовують просунуте обладнання майнингу (GPU та ASIC) для майнингу на тестнеті. Це підвищує складність, роблячи неможливим майнинг за допомогою CPU, та з часом роблячи досить складним отримання тестових монет, так що люди починають цінувати їх, так що вони вже дечогось варті. Як результат, час від часу мережа testnet має бути очищеною та рестартованою, з нового блоку створіння, скидаючи складність.
Поточний testnet має назву testnet3, третя ітерація testnet, рестартована в лютому 2011го року, щоб скинути складність від попереднього testnet. Майте на увазі, що testnet3 є великим блокчейном, що перевищує 20Гб на початок 2017го року. Вона займе день для синхронизації, та завантажить ресурси вашого комп'ютера. Не така велика як mainnet, але вже точно не “легковажна”. Один гарний спосіб запустити вузол testnet є використання образу віртуальної машини (тобто, VirtualBox, Docker, Cloud Server, тощо), виділеної для ціх цілей.
Bitcoin Core, як майже любе інше програмне забезпечення біткоін, має повну підтримку для операцій з testnet, замість mainnet, але також дозволяє вам майнати тестові монети, та оперувати повним вузлом testnet.
Щоб запустити Bitcoin Core на testnet замість mainnet, ви використовуєте ключ testnet:
$ bitcoind -testnet
В ваших журналах ви повинні побачити, що bitcoind будує новий блокчейн в субкаталозі testnet3 директорії по замовчанню bitcoind:
bitcoind: Using data directory /home/username/.bitcoin/testnet3
Щоб з'єднатись до bitcoind, ви використовуєте інструмент командного рядка
bitcoin-cli, але вам також треба перемикнутись в режим testnet:
$ bitcoin-cli -testnet getinfo
{
"version": 130200,
"protocolversion": 70015,
"walletversion": 130000,
"balance": 0.00000000,
"blocks": 416,
"timeoffset": 0,
"connections": 3,
"proxy": "",
"difficulty": 1,
"testnet": true,
"keypoololdest": 1484801486,
"keypoolsize": 100,
"paytxfee": 0.00000000,
"relayfee": 0.00001000,
"errors": ""
}
Також ви можете іикористовувати команду getblockchaininfo, що
підтвердити деталі мережі testnet3 та ваш прогрес синхронізації:
$ bitcoin-cli -testnet getblockchaininfo
{
"chain": "test",
"blocks": 1088,
"headers": 139999,
"bestblockhash":
"0000000063d29909d475a1c4ba26da64b368e56cce5d925097bf3a2084370128",
"difficulty": 1,
"mediantime": 1337966158,
"verificationprogress": 0.001644065914099759,
"chainwork": "0000000000000000000000000000000000000000000000000000044104410441",
"pruned": false,
"softforks": [
[...]
Також ви можете робити з testnet3 за допомогою інших повно-вузлових
реалізацій, таких, як btcd (написаний на Go), bcoin (написаний на
JavaScript), щоб експеріментувати та навчатись в інших програмних мовах та
фреймворках. На початок 2017го року, testnet3 підтримує всі можливості
mainnet, на додаток до Segregated Witness (дивіться Додаток D), що ще має
бути активований на mainnet. Таким чином, testnet3 може також бути
використаний для тестування можливостей Segregated Witness.
В 2016му році була запущена тестова мережа спеціального призначення, щоб допомогти в розробці та тестуванні Segregated Witness (скорочено segwit; дивіться Додаток D). Це блокчейн, названий segnet, та може бути під'єднаний через виконання спеціальної версії (відгалуження) Bitcoin Core. Оскільки segwit був доданий до testnet3, більше не є необхідним використовувати segnet для тестування можливостей segwit. В майбутньому вірогідно ми побачимо інші блокчейни testnet, що спеціально розроблені для тестування окремої можливості або важливої архитектурної зміни, як segnet.
Regtest, що означає “Regression Testing”, є можливістю Bitcoin Core, що дозволяє вам створити локальний блокчейн для цілей тестування. На відміну від testnet3, що є публічним та загальним блокчейном, блокчейни regtest призначені для виконання як зачинена система для локального тестування. Ви запускаєте блокчейн regtest з самого початку, створюючи локальний блок творення. Ви можете додати інші вузли до мережі, або виконати її на окремому вузлі, тільки для тестування програмного забезпечення Bitcoin Core.
Щоб запустити Bitcoin Core в режимі regtest, ви можете використовувати флаг regtest:
$ bitcoind -regtest
Так само, як з testnet, Bitcoin Core буде ініціалізувати новий блокчейн в субдиректорії regtest вашої директорії bitcoind по замовчанню:
bitcoind: Using data directory /home/username/.bitcoin/regtest
Щоб задіяти інструмент командного рядка, вам треба вказати також флаг regtest. Давайте спробуємо команду getblockchaininfo для дослідження блокчейну regtest:
$ bitcoin-cli -regtest getblockchaininfo
{
"chain": "regtest",
"blocks": 0,
"headers": 0,
"bestblockhash":
"0f9188f13cb7b2c71f2a335e3a4fc328bf5beb436012afca590b1a11466e2206",
"difficulty": 4.656542373906925e-10,
"mediantime": 1296688602,
"verificationprogress": 1,
"chainwork": "0000000000000000000000000000000000000000000000000000000000000002",
"pruned": false,
[...]
Як ви можете бачити, досі немає жодних блоків. Давайте намайнаємо
декілька (500 блоків), та отримаємо винагороду:
$ bitcoin-cli -regtest generate 500
[
"7afed70259f22c2bf11e406cb12ed5c0657b6e16a6477a9f8b28e2046b5ba1ca",
"1aca2f154a80a9863a9aac4c72047a6d3f385c4eec5441a4aafa6acaa1dada14",
"4334ecf6fb022f30fbd764c3ee778fabbd53b4a4d1950eae8a91f1f5158ed2d1",
"5f951d34065efeaf64e54e91d00b260294fcdfc7f05dbb5599aec84b957a7766",
"43744b5e77c1dfece9d05ab5f0e6796ebe627303163547e69e27f55d0f2b9353",
[...]
"6c31585a48d4fc2b3fd25521f4515b18aefb59d0def82bd9c2185c4ecb754327"
]
Це займає лише декілька секунд, щоб намайнати всі ці блоки, що однозначно робить це простим для тестування. Якщо ви перевірите баланс вашого гаманця, ви побачите, що ви отримали винагороду за перші 400 блоків (винагорода коінбейс має мати 100 блоків в глибину, перед тим, як вона може бути витрачена):
$ bitcoin-cli -regtest getbalance
12462.50000000
Різні блокчейни біткоін (regtest, segnet, testnet3, mainnet) надають диапазон тестових оточень для робобки біткоін. Використовуйте тестовий блокчейн для розробки біткоін. Використовуйте тестові блокчейни, коли ви розробляєте для Bitcoin Core, або іншого повно-вузлового клієнта; застосування, такого як гаманець, обмін, сайт онлайн комерції; або навіть розробки новітніх контрактів або складних скриптів.
Ви можете використовувати тестові блокчейни для встановлення
розробницьгого середовища. Тестуйте ваш код локально на regtest по мірі
розробки. Коли ви станете готові щоб спробувати його на публічній мережі,
перемикайтесь до testnet щоб показати ваш код в більш динамічному
оточенні, з більшою різноманітністю коду та застосувань. Нарешті, коли ви
досить переконались, що ваш код робить як очікувалось, перемикайтесь на
mainnet, щоб розгорнути його в продакшині. Якщо ви зробите зміни,
покращення, виправлення помилок, тощо, почните знову все з початку,
розгортаючи кожну зміну на regtest, потім на testnet, та нарешті в
продукцію.
Слово "майнинг" є дещо недолуге. Через походження від добування цінних металів, воно фокусує нашу увагу на винагороді за майнинг, новий біткоін, створений в кожному блоці. Хоча майнинг стимульований через винагороду, первинне призначення майнингу є не винагорода або генерація нових монет. Якщо ви дивитесь на майнинг лише як на процес, як створюються нові монети, ви плутаєте засоби (стимули) як ціль процесу. Майнинг є механізмом, що створює децентралізований кліринговий центр, де транзакції валідуються та очищуються. Майниг є винаходом, що робить біткоін особливим, децентралізованим механізмом безпеки, що є основою для цифрових грошей P2P.
Майнинг унебезпечує систему біткоіна, та робить можливим виникнення ціло-мережевого консенсуса, без центрального впливу. Винагорода за тільки но відкарбовані монети, та комісія за транзакції, є схемою заохочення, що підлаштовує дії майнерів до безпеки мережі, в той же час реалізуючи надходження монет. Призначення майнингу не є створення нового біткоіна. Це система заохочення. Майнинг є механізм, завдяки якому біткоін є безпечним та децентралізованим.
Майнери перевіряють нові транзакції, та записують їх в глобальний реєстр. Новий блок, що містить транзакції, які відбулись після останнього блоку, в середньому "майнаються" кожні 10 хвилин, додаючи ці транзакції до блокчейну. Транзакції, що стали частиною блоку, та додані до блокчейну, розглядаються як “підтверджені”, що дозволяє новим власникам біткоіну витрачати біткоіни, що вони щойно отримали, в своїх транзакціях.
Майнери отримують два типи винагород за безпеку, що вони провадять через майнинг: нові монети, створені в кожному блоці, та комісійні за транзакцію від всіх транзакцій, що включені в блок. Щоб отримати ці винагороди, майнери змагаються для вирішення складної математичної проблеми, базованої на алгоритмі криптографічного хешу. Рішення проблеми, що називається підтвердженням виконаної роботи, включається в кожний новий блок, та діє як підтвердження, що майнер витратив значні обчислювальні потуги. Змагання за вирішення алгоритму підтвердження виконанної роботи, щоб отримати винагороду, та право записувати транзакції в блокчейн, є основою моделі безпеки блокчейну.
Процес названий майнингом завдяки нагороді (генерація нової монети)
розроблений стимулювати зменшувані повернення, так само як майнинг для
дорогоцінних металів. Постачання грошей біткоіну створюється через
майнинг, подібно до того, як центральний банк випускає нові гроші через
друк банківських білетів. Максимальна кількість нових створених біткоінів,
що майнер може додати до блоку, зменьшується приблизно кожні чотири роки
(якщо точніше, кожні 210,000 блоків ). Вона стартує з 50 біткоінів
на блок в січні 2009, та переділилось до 25 біткоінів за блок в листопаді
2012. Ще раз переділ відбувся до 12.5 біткоінів в липні 2016. Базуючись на
цій формулі, винагороди від майнингу біткоіна зменьшуються
експотенціально, приблизно до року 2140, коли всі біткоіни (20.99999998
мільйонів) будуть в обігу. Після року 2140 нові біткоіни не будуть
надходити.
Майнери біткоіну також отримують комісійні від транзакцій. Кожна транзакція може включати комісійні за транзакцію, в формі різниці біткоінів між входами транзакції та її виходами. Переможний майнер біткоіна отримує право “утримувати різницю” з транзакцій, включених в переможний блок. Сьогодні комісійні складають 0.5% або менше від мінімального надходження біткоін, значна більшість надходить від знову відкарбованих монет. Однак, докі винагорода зменшуватиметься з часом, та число транзакцій на блок збільшується, все більша частина доходів від майнингу буде приходитись на комісійні. Поступово, винагорода майнингу буде домінувати для комісійних від транзакцій, що буде формувати первинне заохочення для майнерів. Після 2140го року, число нових біткоінів в кожному блоці впаде до нуля, тамайнинг біткоіну буде заохочуватись тільки комісійними з транзакцій.
В цій главі ми спочатку переглянемо майнинг як механізм монетарного
забезпечення, та потім поглянемо на найбільш важливі функції майнингу:
механізм децентралізованого консенсусу, що складає безпеку біткоіну.
Щоб зрозуміти майнинг та консенсус, ми будемо слідувати за транзакцією
Аліси, коли вона була отримана, та додана до блоку майнинговим обладнанням
Джінга. Потім ми послідкуємо за блоком, як він був змайнаний, доданий до
блокчейну, та сприйнятий мережею біткоін через процес утворення
консенсусу.
Біткоін “карбується” впродовж створення кожного нового блоку, з фіксованою та зменшуваною частотою. Кожний блок, згенерований в середньому кожні 10 хвилин, містить повністю новий біткоін, створений з нічого. Кожні 210000 блоків, або приблизно кожні чотири роки, вихід грошей зменьшується на 50%. Для перших чотирьох років діяльності мережі, кожний блок складав 50 нових біткоінів. В листопаді 2012 нова частота утворення біткоінів склала 25 біткоінів на блок. В липні 2016 вона скоротилась знову, до 12.5 біткоінів на блок. Вона буде знову переділена до 6.25 біткоінів на блоці 630,000, що буде змайновано десь в 2020му році. Частота нових монет зменьшується таким чином до 32 “розполовинень”, доки блок 6720000 не буде змайнаний приблизно в 2137му, та тоді він досягне мінімума одиниці виміру в 1 сатоші. Нарешті, після 6.93 мільйонів блоків, або приблизно в 2140му році, близько 2,099,999,997,690,000 сатоші, або майже 21 мільйонів біткоінів, будуть видані в світ. Після цього, блоки не будуть містити нових біткоінів, та майнери будуть отримувати винагороду виключно через камісії з транзакцій. Малюнок 10-1 показує загальні біткоіни в обертанні з часом, по мірі зменшення їх випуску.
Малюнок 10-1. Надходження грошей біткоін з часом, на основі геметричного
зменшення частоти їх надходження
Максимальним числом монет, що змайнані, є обмеження верхнього ліміту
винагороди за майнінг. На практиці, майнер може навмисне змайнати блок,
заберучи меньше, ніж повна винагорода. Такі блоки вже насправді були
змайнані, та ще можуть бути змайнані в майбутньому, що призведе до
зменшення загальної кількості грощей в оберті.
В пркладі коду Приклад 10-1, ми обчислюємо загальну кількість біткоіну,
що буде випущений.
Приклад 10-1. Скрипт для обчислення, як багато бітеоінів буде випущено
# Оригінальна винагорода за блок для майнерів була 50 BTC
start_block_reward = 50
# 210000 є обертається кожні 4 роки з 10 хвилинним інтервалом на блок
reward_interval = 210000
def max_money():
# 50 BTC = 50 0000 0000 Satoshi
current_reward = 50 * 10**8
total = 0
while current_reward > 0:
total += reward_interval * current_reward
current_reward /= 2
return total
print "Total BTC to ever be created:", max_money(), "Satoshis"
Приклад 10-2 показує результат роботи цього скрипта.
Приклад 10-2. Виконання скрипта max_money.py
$ python max_money.py
Total BTC to ever be created: 2099999997690000 Satoshis
Обмежений та зменшуваний випуск створює фіксоване постачання грошей, що чинить опір інфляції. На відміну від вільних грошей, що можуть бути надруковані в необмеженій кількості центральним банком, біткоін ніколи не піддасться інфляції через друк.
Найбільш важливе та спірний наслідок фіксованого та зменшуваного монетарного випуску є те, що валюта має тенденцію бути природно дефляційною. Дефляція це феномен підвищення значення через невідповідність між постачанням та попитом, що взвинчує значення (та рівень обміну) валюти. На протилежність до інфляції, цінова дефляція означає, що гроші набувають більшу купівельну спроможність з часом. Багато економістів аргументують, що дефляційна економіка є безлад, якого треба уникати за любу ціну. Це так, тому що в період швидкої дефляції люди схильні накопичувати гроші, а не витрачати їх, очікуючи, що ціни мають впасти. Такий феномен бів викритий під час “пропащого десятиліття” в Японії, коли повний колапс попиту зіштовхнув валюту в дефляційну спіраль.
Експерти біткоін аргументують, що це не так погано само по собі. Скоріше, дефляція асоційована з колапсом попиту, оскільки це тільки один з прикладів дефляції, що миємо вивчити. З неприв'язаною валютою, з можливістю беобмеженого друку, дуже складно увійти в дефляційну спіраль, тільки якщо не буде повного колапсу з попитом, та небажання друкувати гроші. Дефляція біткоіну не викликаєтсья колапсом у попиті, але передбачуваним обмеженним постачанням.
Позитивний аспект дефляції, звичайно, в тому, що це протилежність інфляції. Інфляція спричиняє повільне, але неминуче знецінення валюти, що призводить до форми прихованного оподаткування, якім обкладаються накопичувачі, щоб врятувати боржників (включаючи найбільших боржників, самі уряди). Валюта під контролем уряду потерпає від моральної загрози простого створення боргів, що потім можуть бути легко погашені через знецінення, за рахунок накопичувачів.
Залишається побачити, чи дефляційний аспект валюти є проблемою, коли його рушій не швидке згортання економіки, або це перевага, оскільки це захист від інфляції та знецінення, що переважає ризики дефляції.
В попередній главі ми дивились на блокчейн, глобальний публічний реєстр (список) всіх транзакцій, який кожний в мережі біткоін сприймає як авторитетний запис щодо власності. Але як може кожен в мережі погодитись з єдиною універсальною “правдою” щодо того, хто володіє чим, не довіряючи при цьому нікому? Всі традиційні платіжні системи залежать від моделі довіри, що має центральну інстранцію, та провадить послуги підтвердження, в основі верифікуючи та підтверджуючи всі транзакції. Біткоін не має центральної інстанції, та все одно кожний повний вузол має повну копію публічного облікового реєстра, якому він може довіряти як авторитетному запису. Блокчейн не створений центральною інстанцією, але збирається незалежно кожним вузлом в мережі. Якимось чином, кожний вузол в мережі, діючи з інформацією, переданою по небезпечним мережевим з'єднанням, може дійти того самого висновку, та зібрати копію того самого публічного реєстра, що і кожний інший. Ця глава перевіряє процес, завдяки якому мережа біткоін досягає глобального консенсусу без центрального довіреного органа.
Головний винахід Satoshi Nakamoto є децентралізований механізм для виникнення консенсусу. Виникнення, бо консенсус не досягається явним чином — немає голосування, або фіксованого моменту, коли настає консенсус. Змість цього, консенсус є виникаючим артифактом від асинхронних інтеракцій тисячів незалежних вузлів, що всі слідують простим правилам. Всі властивості біткоіна, включаючи валюту, транзакції, платежі, та модель безпеки, що не спирається на центральний інструмент довіри, походять з цього винаходу.
Децентралізований консенсус біткоін виникає з взаємодії чотирьох
процесів, що відбуваються незалежно на вузлах по всій мережі:
• Незалежна верифікація кожної транзакції, кожним повним вузлом, базуючись
на виключному списку крітерій
• Незалежна агрегація ціх транзакцій в нові блоки майнаючими вузлами,
разом з демонстрацією обчислень через алгоритм доказу виконаної роботи
• Незалежна верифікація нових блоків на кожному вузлі, та збирання їх в
блокчейн
• Незалежний вибір кожним вузлом ланцюга з найбільшим кумулятивним
обчисленням, що демонструється через доказ виконаної роботи
В декількох наступних розділах ми будемо досліджувати ці процеси, та як вони взаємодіють для створення виникаючої властивості мережевого консерсусу, що дозволяє вузлу біткоін зібрати власну копію довіреного, публічного, глобального реєстра.
В Главі 6 ми бачили, як програмний гаманець створює транзакції через збирання UTXO, провадячи відповідний розблокуючий скрипт, та потім конструюючі нові виходи, призначені для нового власника. Результуюча транзакція потім надсилається до сусідніх вузлів в мережі біткоін, так що вони можуть просуватись по всій мережі біткоін.
Однак перед передачею транзакцій до сусідів, кожний вузол біткоін, що отримує транзакцію, спершу має перевірити транзакцію. Це переконує, що тільки двалідні транзакції просуваються по мережі, тоді як невалідні транзакції відкидаються на першому ж вузлі, який виявить їх.
Кожний вузол перевіряє кожну транзакцію згідно списку заданих критерій:
• Синтаксис транзакції та структура даних має бути коректною.
• Вхідні та вихідні списки не порожні.
• Розмір транзакції в байтах меньше ніж MAX_BLOCK_SIZE.
• Кожне вихідне значення, так само як і загал, має бути в допустимому
диапазоні значень (меньше ніж 21 мільйонів монет, меньше ніж поріг пилу).
• Ніякий зі входів не має хеш рівним 0, N=–1 (транзакції коінбейсу не
повинні пересилатись).
• nLocktime рівне INT_MAX, або значення nLocktime та nSequence
задовільняють відповідно до MedianTimePast.
• Розмір транзакції в байтах більше ніж, або дорівнює 100.
• Число операцій сигнатури (SIGOPS), що міститься в транзакції, є меньшим,
ніж обмеження на операції сигнатури.
• Розблокуючий скрипт (scriptSig) може заштовхувати в хеш лише числа, та
блокуючий скрипт (scriptPubkey) має співпадати з формами isStandard (це
відхиляє “нестандартні” транзакції).
• Має існувати співпадаюча транзакція в пулі, або в блоці в головній
вітці.
• Для кожного входу, якщо відповідний вихід існує в любій іншій транзакції
в пулі, транзакція має бути відхилена.
• Для кожного входу передивитись головну вітку та пул транзакцій, в
пошуках відповідної вихідної транзакції. Якщо вихідна транзакція відсутня
для любого входу, це буде загублена транзакція. Вона додається до пулу
загублених, якщо така транзакція вже не знаходиться в пулі.
• Для кожного входу, якщо посилана вихідна транзакція є вихідом коінбейсу,
вона повинна мати щонайменьше COINBASE_MATURITY (100) підтворджень.
• Для кожного входу, відповідний вихід має існувати, та не може бути вже
витраченим.
• Використовуючи посилані виходи транзакції щоб отримати вхідні значення,
перевіряється, що кожне вхідне значення, так само, як і сума, знаходиться
в дозволеному диапазоні значень (менше 21 мільйона, більше ніж 0).
• Відхилити, якщо сума значень входів меньша, ніж сума значень виходів.
• Відхилити, якщо комісійні по транзакції будуть дуже низькими
(minRelayTxFee), щоб опинитись в порожньому блоці.
• Розблокуючі скрипти для кожного входу мають валідуватись згідно
відповідних вихідних блокуючих скриптів.
Ці умови можуть бути побачені в деталях в функціях AcceptToMemoryPool, CheckTransaction, та CheckInputs в Bitcoin Core. Зауважте, що умови змінюються з часом, щоб відповідати новим типам атак відмови в обслуговуванні, або іноді для пом'якшення правил, так, щоб включити більшу кількість транзакцій.
Незалежно перевіряючі кожну транзакцію по мірі надходження, та перед просуванням її далі, кожний вузол будує пул валідних (але непідтверджених) транзакцій, відомих як пул транзакцій, пул в пам'яті або mempool.
Деякі з вузлів в мережі біткоін є спеціалізованими вузлами, що називаються майнерами. В Главі 1 ми познайомились з Джингом, комп'ютерним студентом-інженером з Шанхаю, Китай, який є майнером біткоін. Джинг заробляє біткоін, запустивши “майнаючу установку”, що є спеціалізованою апаратною системою, розробленою для майнінгу біткоінів. На відміну від Джинга, деякі майнери майнять без повного вузла, як ми бачили в “Майнінгових пулах”. Як кожний інший вузол, вузол Джинга отримує та просуває непідтверджені транзакції в мережі біткоін. Однак вузол Джинга також збирає ці транзакції в нові блоки. Вузол Джинга слухаж щодо нових блоків, що передаються мережею біткоін, як це роблять всі вузли. Однак поява нового блоку має особливе значення для майнаючого блока. Змагання між майнерами ефективно завершується просуванням нового блоку, що діє як анонс на користь переможця. Для майнерів отримання валідного нового блоку означає, що хтось інший переміг в змаганні, а вони програли. Однак кінець одного раунду також є початком наступного раунду. Новий блок не тільки фінішний флаг, що позначає завершення перегонів; він також стартовий пістолет, що починає перегони за новим блоком.
Після валідації транзакцій вузол біткоін додасть її до пулу в пам'яті, або пулу транзакцій, де транзакції будуть очікувати, доки вони не зможуть бути включені (змайнені) в блок. Вузол Джинга збирає, перевіряє, та пересилає нові транзакції, так само, як кожний інший вузол. Однак на відміну від інших вузлів, вузол Джинга буде агрегувати ці трензакції в блок-кандидат.
Давайте прослідимо з блоками, що були створені під час того, як Аліса купила філіжанку кави в кафе Боба (дивіться “Купляючи філіжанку кави”). Транзакція Аліси була включена в блок 277,316. Для цілей демонстрації концепцій в цій главі, давайте вважати, що блок був смайнаний системой майнинга Джинга, та послідуємо за транзакцією Аліси, коли вона стає частиною нового блоку.
Вузол майнингу Джинга підтримує локальну копію блокчейна. Коли Аліса купляє свою каву, вузол Джинга зібрав ланцюг аж до блока 277,314. Вузол Джинга слухає щодо транзакцій, намагаючись змайнати новий блок, а також слухає щодо блоків, винайдених іншими вузлами. Якщо вузол Джинга майнить, він отримає блок 277,315 по мережі біткоін. Надходження цього блоку означає кінець зманання за блок 277,315, та початок змагання за створення блока 277,316.
На протязі попередніх 10 хвилин, доки вузол Джинга шукав рішення для блока 277,315, він також збирав транзакції в підготовці до нового блока. Тепер він назбирав декілька сотен транзакцій в пулі в пам'яті. Під час отримання блоку 277,315, та його валідації, вузол Джинга також порівнює його з усіма транзакціями в пулі в пам'яті, та видаляє всі, що включені в блок 277,315. Таким чином транзакції, що залишились в пулі є непідтвердженими, та очікують на запис в новий блок.
Вузол Джинга безпосередньо конструює новий порожній блок, кандидата на блок 277,316. Цей блок називається блоком-кандидатом, тому що він досі не є валідним блоком, бо він не містить валідний доказ виконаної роботи. Цей блок стає валідним тільки якщо майнеру вдасться знайти рішення алгоритму доказу виконанної роботи.
Коли вузол Джинга агрегує всі транзакції з пула в пам'яті, новий
блок-кандидат має 418 транзакцій, з загальною комісією за транзакції в
0.09094928 біткоінів. Ви можете побачити цей блок в блокчейні,
використовуючи клієнт Bitcoin Core з інтерфейсом командного рядка, як
показано в Прикладі 10-3.
Приклад 10-3. Використання командного рядка для отримання блока 277,316
$ bitcoin-cli getblockhash 277316
0000000000000001b6b9a13b095e96db41c4a928b97ef2d944a9b31b2cc7bdc4
$ bitcoin-cli getblock 0000000000000001b6b9a13b095e96db41c4a928b97ef2d9\
44a9b31b2cc7bdc4
{
"hash" : "0000000000000001b6b9a13b095e96db41c4a928b97ef2d944a9b31b2cc7bdc4",
"confirmations" : 35561,
"size" : 218629,
"height" : 277316,
"version" : 2,
"merkleroot" :
"c91c008c26e50763e9f548bb8b2fc323735f73577effbc55502c51eb4cc7cf2e",
"tx" : [
"d5ada064c6417ca25c4308bd158c34b77e1c0eca2a73cda16c737e7424afba2f",
"b268b45c59b39d759614757718b9918caf0ba9d97c56f3b91956ff877c503fbe",
... 417 more transactions ...
],
"time" : 1388185914,
"nonce" : 924591752,
"bits" : "1903a30c",
"difficulty" : 1180923195.25802612,
"chainwork" :
"000000000000000000000000000000000000000000000934695e92aaf53afa1a",
"previousblockhash" :
"0000000000000002a7bbd25a417c0374cc55261021e8a9ca74442b01284f0569"
}
Перша транзакція в любому блоці є спеціальною транзакцією, що
називається коінбейс-транзакцією. Ця транзакція сконструйована вузлом
Джинга, та містить його винагороду за потуги по майнингу. Коли блок
277,316 був змайнаний, винагорода була 25 біткоін на блок. З тих пір
пройшов один період "переділу". Винагорода за блок змінилась до 12.5
біткоінів в липні 2016. Вона буде переділена знову через 210,000 блоків, в
2020 році.
Вузол Джинга створює коінбейс транзакцію як платіж до свого власного гаманця: “Сплатити на адресу Джинга 25.09094928 біткоінів”. Загальна сума винагороди, що назбирає Джинг від майнингу блока, є сумою винагороди коінбейсу (25 нових біткоінів), та комісійні за транзакції (0.09094928) з усіх транзакцій, що включені в блок, як показано в Прикладі 10-4.
Приклад 10-4. Коінбейс транзакція
$ bitcoin-cli getrawtransaction
d5ada064c6417ca25c4308bd158c34b77e1c0eca2a73cda16c737e7424afba2f 1
{
"hex" :
"01000000010000000000000000000000000000000000000000000000000000000000000000ffffffff0
f03443b0403858402062f503253482fffffffff0110c08d9500000000232102aa970c592640d19de03ff
6f329d6fd2eecb023263b9ba5d1b81c29b523da8b21ac00000000",
"txid" : "d5ada064c6417ca25c4308bd158c34b77e1c0eca2a73cda16c737e7424afba2f",
"version" : 1,
"locktime" : 0,
"vin" : [
{
"coinbase" : "03443b0403858402062f503253482f",
"sequence" : 4294967295
}
],
"vout" : [
{
"value" : 25.09094928,
"n" : 0,
"scriptPubKey" : {
"asm" :
"02aa970c592640d19de03ff6f329d6fd2eecb023263b9ba5d1b81c29b523da8b21OP_CHECKSIG",
"hex" :
"2102aa970c592640d19de03ff6f329d6fd2eecb023263b9ba5d1b81c29b523da8b21ac",
"reqSigs" : 1,
"type" : "pubkey",
"addresses" : [
"1MxTkeEP2PmHSMze5tUZ1hAV3YTKu2Gh1N"
]
}
}
]
}
На відміну від звичайних транзакцій, коінбейс транзакція не споживає (витрачає) UTXO на вході. Замість цього вона має тільки один вхід, що називається коінбейсом, що створює біткоіни з нічого. Транзакція коінбейс має один вихід, яким може сплатити майнер з власної адреси. Вихід транзакції коінбейс надсилає значення 25.09094928 біткоінів на біткоін адресу майнера; в цьому випадку це 1MxTkeEP2PmHSMze5tUZ1hAV3YTKu2Gh1N.
Щоб побудувати коінбейс транзакцію, вузол Джинга спершу обчислює загальну суму комісійних, додаючи всі входи та виходи для 418 транзакцій, що додані до блоку. Комісійні ообчислюються як:
Щагальні комісійні = Sum(Входи) - Sum(Виходи)
В блоці 277,316 загальні комісійні по транзакціях складають 0.09094928
біткоінів. Далі вузол Джинга обчислює коректну винагороду за новий блок.
Винагорода обчислюється на основі висоти нового блоку, починаючи з 50
біткоінів за блок, та зменшуючись на половину кожні 210,000 блоків.
Оскільки цей блок на висоті 277,316, коректна винагорода складає 25
біткоінів. Калькуляцію можна побачити в функції GetBlockSubsidy клієнта
Bitcoin Core, як показано в Прикладі 10-5.
Приклад 10-5. Обчислення винагороди за блок — функція GetBlockSubsidy, клієнт Bitcoin Core, main.cpp
CAmount GetBlockSubsidy(int nHeight, const Consensus::Params& consensusParams)
{
int halvings = nHeight / consensusParams.nSubsidyHalvingInterval;
// Force block reward to zero when right shift is undefined.
if (halvings >= 64)
return 0;
CAmount nSubsidy = 50 * COIN;
// Subsidy is cut in half every 210,000 blocks which will occur approximately every 4 years.
nSubsidy >>= halvings;
return nSubsidy;
}
Початкова субсидія, обчислена в сатоші, та помножена на 50 за допомогою константи COIN (100,000,000 сатоші). Це встановлює початкову винагороду (nSubsidy) в 5 мільйонів сатоші. Далі, функція обчислює число переділень, що відбуваються діленням поточної висоти блоку на інтервал переділення(SubsidyHalvingInterval). В випадку блоку 277,316, з інтервалом переділення кожні 210,000 блоків, результатом буде 1 переділення.
Максимальне число переділень є 64, так що код видасть нульову винагороду (не враховуючи комісійних), якщо число переділень перевищить 64. Далі, функція використовує оператор бінарного правого зсуву, щоб поділити винагороду (nSubsidy) на два для кожного раунду переділення. В випадку блоку 277,316, це буде правий зсув винагороди в 5 мільйонів сатоші (один раз), що дасть 2,5 мільйони сатоші, або 25 біткоінів. Оператор бінарного правого зсуву, бо він більш ефективний, ніж ділення на основі множення. Щоб уникнути потенційного багу, операція зсуву пропускається після 63 переділень, та субсидія встановлюється в 0. Нарешті, коінбейс винагорода (nSubsidy) додається до комісійних за транзакції (nFees), та повертається сума.
Якщо майнинговий вузол Джинга записує транзакцію коінбейсу, що зупиняє Джинга від "винагоди" себе в 100 або 1000 біткоінів? Відповідь в тому, що невірна винагорода призведе до того, що блок вважатиметься невалідним усіма іншими, та втрати електричної енергії Джинга, витраченої на обчислення доказу виконаної роботи. Джинг зможе витратити винагорооду тільки в випадку, коли блок буде сприйнятий всіма і кожним.
З ціма розрахунками, вузол Джинга конструює коінбейс транзакцію, щоб сплатити собі 25.09094928 біткоінів. Як ви бачили в Прикладі 10-4, коінбейс транзакція має особливий формат. Замість того, щоб вхід транзакції вказував на витрату попереднього UTXO, це є входом “коінбейс”. Ми перевірили входи транзакції в Таблиці 6-2. Давайте порівняємо звичайний вхід транзакції з входом транзакції коінбейс. Таблиця 10-1 показує структуру звичайної транзакції, тоді як Таблиця 10-2 показує структуру входу транзакції коінбейс.
Таблиця 10-1. Структура "нормального" входу транзакції
| Розмір | Поле | Опис |
| 32 байти | Хеш транзакції | Вказівник на транзакцію, що містить UTXO, яке витрачається |
| 4 байти | Індекс виходу | Числовий індекс UTXO, що витрачається, починаючи з 0 |
| 1-9 байт(VarInt) | Розмір розблокуючого скрипта | Довжина відмикаючого скрипта в байтах |
| змінний | Розблокуючий скрипт | Скрипт, що задовільняє умовам замикаючого скрипта UTXO |
| 4 байти | Послідовний номер | Наразі відключена можливість Tx-заміни, встановлено в 0xFFFFFFFF |
Таблиця 10-2. Структура входу транзакції коінбейс
| Розмір |
Поле |
Опис |
| 32 байти |
Хеш транзакції |
Всі біти нульові, посилання на транзакцію відсутнє |
| 4 байти |
Індекс виходу |
Всі біти одиниці: 0xFFFFFFFF |
| 1-9 байт(VarInt) | Розмір даних коінбейс |
Довжина даних коінбейс, від 2 до 100 байт |
| змінний |
Дані коінбейс |
Довільні дані, що використовуються як додатковий довісок та теги майнингу. В блоках версії v2 має починатись з висоти блока |
| 4 байти |
Послідовний номер |
Встановлено в 0xFFFFFFFF |
В транзакції коінбейс, перші два поля встановлені в значення, що не
представляють посилання на UTXO. Замість “хеша транзакції” перше поле
заповнене 32 байтами нулів. “Вихідний індекс” заповнений 4 байтами одиниць
0xFF (255 в десятичній системі). “Розблокуючий скрипт” (scriptSig)
замінений на дані коінбейс, поле даних для майнерів, як ви побачите далі.
Транзакції коінбейс не мають поля розблокуючого скрипта (scriptSig). Замість цього це поле замінене на дані коінбейс, що має бути від 2 до 100 байтів. За винятком перших декількох байтів, залишок даних коінбейс може використовуватись майнерами як вони цього побажають. Це довільні дані.
В блоці творення, наприклад, Satoshi Nakamoto додав текст “The Times 03/Jan/2009 Chancellor on brink of second bailout for banks” в дані коінбейс, використавши це як доказ дати, та надіслення повідомлення. Наразі майнери використовують дані коінбейс для включення додаткового значення довіску, та рядка, що ідентифікує майнинговий пул.
Перші декілька байтів коінбес були довільними свого часу, але це вже не так. Згідно BIP-34, блоки версії 2 (блоки з полемверсії в значенні 2) мають містити індекс висоти блоку, в вигляді операції скрипта “push” на початку поля коінбейс.
В блоці 277,316 ми бачимо, що коінбейс (дивіться Приклад 10-4), що є в розблокуючому скрипті, або полі scriptSig входу транзакції, містить шістнадцятиричне значення 03443b0403858402062f503253482f. Давайте розкодуємо це значення. Перший байт, 03, інструктує скриптову машину заштовхати наступні три байти в стек скрипта (дивіться Таблицю B-1). Наступні три байти, 0x443b04, є висотою блока, закодованого в форматі little-endian (зворотньому, найменьш значущий байт перший). Обертаючи порядок байтів в результаті дає 0x043b44, що в десятичному вигляді є 277,316. Наступні декілька цифр (0385840206) використовуються як додатковий довісок (дивіться “Рішення додаткового довіску”), або випадкове значення, що використовується для пошуку підходящого рішення підтвердження виконаної роботи.
Заключна частина даних коінбейсу (2f503253482f) є ASCII-кодованим рядком
/P2SH/, що вказує, що майнінговий вузол, що змайнав цей блок, підтримує
покращення P2SH .визначене в BIP-16. Всутп до можливостей P2SH потребує
сигналювання майнерами про підтримку або BIP-16, або BIP-17. Це
підтвердження реалізації BIP-16 надійшло через включення /P2SH/ в їх дані
коінбейс. Підтвердження реалізації BIP-17 P2SH буде виглядати як рядок
p2sh/CHV в їх даних коінбейсу. BIP-16 бвв обраний як переможець, та багато
майнерів продовжують включати рядок /P2SH/ в сій коінбейс, щоб вказати
свою підтримку цієї можливості.
Приклад 10-6 використовує libbitcoin, введену в “Альтернативні клієнти, бібліотеки та тулкіти”, щоб виділити дані коінбейс з блоку творення, відобразивши повідомлення Satoshi. Зауважте, що бібліотека libbitcoin містить статичну копію блоку творення, так що приклад може отримати блок напряму з бібліотеки.
Приклад 10-6. Отримання даних коінбейс з блоку творення
/* Відображуємо повідомлення Satoshi з блоку творення. */
#include <iostream>
#include <bitcoin/bitcoin.hpp>
int main()
{
// Створюємо блок творення.
bc::chain::block block = bc::chain::block::genesis_mainnet();
// Блок творення містить єдину транзакцію коінбейс.
assert(block.transactions().size() == 1);
// Отримуємо першу транзакцію в блоці (коінбейс).
const bc::chain::transaction& coinbase_tx = block.transactions()[0];
// Транзакція коінбейс має один вхід.
assert(coinbase_tx.inputs().size() == 1);
const bc::chain::input& coinbase_input = coinbase_tx.inputs()[0];
// Конвертуємо вхідний скрипт на сирий формат.
const auto prefix = false;
const bc::data_chunk& raw_message = coinbase_input.script().to_data(prefix);
// Конвертуємо на std::string.
std::string message(raw_message.begin(), raw_message.end());
// Відображуємо повідомлення з блоку творення.
std::cout << message << std::endl;
return 0;
}
Ми компілюємо код за допомогою компілятора GNU C++, та виконуємо
отриману програму, як показано в Прикладі 10-7.
Приклад 10-7. Компіляція та виконання коду приклада satoshi-words
$ # Compile the code
$ g++ -o satoshi-words satoshi-words.cpp $(pkg-config --cflags --libs libbitcoin)
$ # Run the executable
$ ./satoshi-words
^D��<GS>^A^DEThe Times 03/Jan/2009 Chancellor on brink of second bailout for banks
To construct the block header, the mining node needs to fill in six
fields, as listed in Table 10-3.
Table 10-3. The structure of the block header
| Розмір |
Поле |
Опис |
| 4 байти | версія | Номер версії для слідкування за оновленнями |
| 32 байти | хеш попереднього блоку | Посилання на хеш попереднього (батьківського) блоку |
| 32 байти | мерклівській корінь | Хеш мерклівського дерева транзакцій в цьому блоці |
| 4 байти | відтиск часу | Приблизний час створення (секунди епохи Юнікс) |
| 4 байти | ціль | Ціль алгоритму доказу виконанохї роботи для цього блока |
| 4 байти | довісок | Безглуздий лічильник, що використовується для підрахунку хеша |
На той час, коли було змайнано блок 277,316, номер версії, що описував
структуру блока, була 2, що закодоване в форматі little-endian в 4 байтах
виглядає так: 0x02000000.
Далі, майнання блоку потребує додавання "Хеш попереднього блоку" (також відомий як pre vhash). Це хеш заголовку блоку 277,315, попереднього блоку, отриманого з мережі, що вузол Джинга прийняв та обрав як батьківській для блока-кандидата блока 277,316. Заголовок блоку для блоку 277,315 такий:
0000000000000002a7bbd25a417c0374cc55261021e8a9ca74442b01284f0569
Обираючи певний батьківській блок, на який вказує хеш попереднього блоку
в блоці-кандидаті, Джинг докладає свою обчислювальну потужність до
розширення ланцюга, що завершується на певний блок. Загалом, це те, як
Джинг "голосує" своєю обчислювальною потужністю за валідний ланцюжок з
найдовшою складністю.
Наступний крок є підсумувати всі транзакції в мерклівське дерево, щоб додати мерклівський корінь до заголовку блока. Транзакція коінбейса вставляється першою транзакцією в блоці. Після неї додані ще інші 418 транзакцій, що разом складає 419 транзакцій в блоці. Як ми бачили в дискусії щодо мерклівських дерев, має бути парне число листів в дереві, так що остання транзакція дублюється, створюючі 420 вузлів, кожен з яких містить хеш однієї транзакції. Хеші транзакцій комбінуються попарно, створюючи нові рівні дерева, доки всі транзакції не складуються в один вузол в "корені" дерева. Корінь мерклівського дерева підсумовує всі транзакції в єдине 32-байтне значення, що ви можете бачити як “merkle root” в Прикладі 10-3, та ми повторимо його тут:
c91c008c26e50763e9f548bb8b2fc323735f73577effbc55502c51eb4cc7cf2e
Майнаючий вузол Джинг потім додасть 4-байтний відтиск часу, закодований в
вигляді "епохи" Юнікс, що базується на числі секунд, що пройшли після 1
січня 1970 року, 0 годин за UTC/GMT. Час 1388185914 відповідає 27 грудня
2013, 23:11:54 за UTC/GMT.
Потім вузол Джинга заповнює ціль, що визначає потрібний доказ виконаної роботи Proof-of-Work, щоб зробити цей блок валідним. Ціль зберігається в блоці як метрика “цільові біти”, що є кодування цілі з мантисою та експонентою. Кодування має 1-байтну експоненту, за якою слідує 3-байтна мантиса (коефіціент). Наприклад, в блоці 277,316, цільові біти є значення 0x1903a30c. Перша частина, 0x19, є шістнацятерична експонента, та далі іде коефіціент, 0x03a30c. Концепція цілі пояснюється в “Зміна цілі та налаштування складності” далі, та представлення “цільових бітів” пояснюється в “Представлення цілі”.
Завершуюче поле є нонс, або довісок, що ініціалізується нулем. Маючи всі ці поля заповненими, заголовок блоку тепер завершений, та можна розпочинати процес майнінгу. Тепер ціль знайти значення для довіску, що дасть хеш заголовку блока, меньший ніж ціль. Майнаючий вузол бепер має перевірити мільярди або трильйони значень довіска, перед тим, як буде знайдений довісок, що задовільнить вимогам.
Тепер, коли блок-кандидат був побудований вузлом Джинга, настає час для обладнання Джинга "змайнати" блок, щоб знайти рішення алгоритма, що робить блок валідним. На протязі цієї книги ми вивчили щодо криптографічних хеш функцій, що використовуються в різних аспектах системи біткоінів. Хеш функція SHA256 є та сама функція, що використовується в процесі майнингу. В простіших термінах, майнинг є процес хешування заголовку блоку раз за разом, змінюючи один параметр, доки отриманий хеш не співпаде з визначеною ціллю. Хеш буде продакувати результат, що не може бути визначений заздалегідь, так само, як не може бути створений шаблон, що утворить бажане хеш значення. Ця властивість хеш функції означає, що єдиний спосіб спродукувати хеш результат, що співпадає з заданою ціллю, є тільки продувати раз за разом, випадково модифікуючи вхід, доки бажаний результат хешу не трапиться випадково.
Алгоритм хешу приймає дані довільної довжини на вході, та продукує детермінистьский результат фіксованої довжини, як відтиск вхідних даних. Для кожного певного входу резльтуючий хеш буде завжди той самий, та може бути просто обчислений та перевірений будь-ким, хто реалізує той самий хеш алгоритм. Ключова характеристика криптографічного хеш алгоритму полягає в обчислювальній неможливості знайти два різні входи, що спродукують той самий відтиск (ситуація, відома як колізія). На відміну, також віртуально неможливо обрати такий вхід, щоб отримати бажаний відтиск, інакше, ніж спробувати випадкові входи.
Алгоритм SHA256 завжди продукує 256 біт довжиною на виході, безвідностно
від довжини входу. В Прикладі 10-8 ми будемо використовувати інтерпретатор
Python для обчислення хешу SHA256 від фрази “I am Satoshi Nakamoto.”
Приклад 10-8. Приклад SHA256
$ python
Python 2.7.1
>>> import hashlib
>>> print hashlib.sha256("I am Satoshi Nakamoto").hexdigest()
5d7c7ba21cbbcd75d14800b100252d5b428e5b1213d27c385bc141ca6b47989e
Приклад 10-8 показує результат обчислення хешу "I am Satoshi Nakamoto":
5d7c7ba21cbbcd75d14800b100252d5b428e5b1213d27c385bc141ca6b47989e.
Це 256-бібтне число є хешем або дайджестом від фрази, та залежить від
кожної частини фрази. Додаючи одну літеру, знак пунктуації, або любі інші
символи, буде продукувати інший хеш. Тепер, якщо ми змінимо фразу, нам
треба очікувати повністю інший хеш. Давайте спробуємо це, через додавання
числа в кінець фрази, за допомогою простого скрипта на Python в Прикладі
10-9.
Приклад 10-9. Скрипт SHA256 для генерації багатьох хешів, через ітерацію
довіску
# приклад ітерації довіску на вході хеш алгоритму
import hashlib
text = "I am Satoshi Nakamoto"
# ітеруємо від 0 до 19
for nonce in xrange(20):
# додаємо довісок до кінця рядка
input = text + str(nonce)
# обчислення SHA-256 для входу (текст+довісок)
hash = hashlib.sha256(input).hexdigest()
# друкуємо результат
print input, '=>', hash
Виконання цього коду продукує хеші для декількох фраз, що додає різни
числа в кінець текста. Через збільшення числа ми отримуємо різні хеші, як
показано в Прикладі 10-10.
Приклад 10-10. Вихід SHA256 скрипта для генерації різноманітних хешей
через ітерацію довіска
$ python hash_example.py
I am Satoshi Nakamoto0 => a80a81401765c8eddee25df36728d732...
I am Satoshi Nakamoto1 => f7bc9a6304a4647bb41241a677b5345f...
I am Satoshi Nakamoto2 => ea758a8134b115298a1583ffb80ae629...
I am Satoshi Nakamoto3 => bfa9779618ff072c903d773de30c99bd...
I am Satoshi Nakamoto4 => bce8564de9a83c18c31944a66bde992f...
I am Satoshi Nakamoto5 => eb362c3cf3479be0a97a20163589038e...
I am Satoshi Nakamoto6 => 4a2fd48e3be420d0d28e202360cfbaba...
I am Satoshi Nakamoto7 => 790b5a1349a5f2b909bf74d0d166b17a...
I am Satoshi Nakamoto8 => 702c45e5b15aa54b625d68dd947f1597...
I am Satoshi Nakamoto9 => 7007cf7dd40f5e933cd89fff5b791ff0...
I am Satoshi Nakamoto10 => c2f38c81992f4614206a21537bd634a...
I am Satoshi Nakamoto11 => 7045da6ed8a914690f087690e1e8d66...
I am Satoshi Nakamoto12 => 60f01db30c1a0d4cbce2b4b22e88b9b...
...
Кожна фраза продукує повністю інших результат хешування. Вони виглядають
повністю довільними, але ви можете відтворити точно такий результат на
любому комп'ютері, за допомогою Python, та побачити ті самі хеші. Число,
використане як змінна в такому сценарії, називається безглуздим довіском,
або нонсом. нонс використовується для зміни виводу криптографічної
функції, в нашому випадку змінювати відтиск SHA256 для ключової фрази.
Щоб зробити змагання з цього алгоритму, давайте встановимо ціль: знайти першу фразу, що продукує шістнадцятиричний хеш, що починається з нуля. На щастя, це не складно! Приклад 10-10 показує, що фраза “I am Satoshi Nakamoto13” продукує хеш:
0ebc56d59a34f5082aaef3d66b37a661696c2b618e62432727216ba9531041a5
Він задовільняє нашому критерію. Щоб знайти його займає 13 спроб. В
термінах вірогідності, якщо вивід функції хешування ріно розподілене, ми
маємо знаходити результат з 0 в якості шістнадцятеричного префіксу кожні
16 хешів (один з 16-ти шістнадцятеричних цифр, від 0 до F). В числових
термінах це означає пошук значення хешу, меньшого ніж
0x1000000000000000000000000000000000000000000000000000000000000000. Ми
назваємо цей відлік приначенням, та ціль полягає в пошуку хешу, що в
числовому сенсі менший, ніж призначення. Якщо ми зменшимо ціль, тоді
рішення пошуку хешу, меншого ніж ціль, стає більш та більш складною.
Щоб отримати просту аналогію, уявіть гру, де гравці раз за разом
викидають пару кісток, намагаючись викинути найменьшу кількість, що меньша
за вказаний рубіж. В мершому раунді ціль є 12. Якщо ви не викидуєте дві
шістірки, ви виграєте. В наступному раунді цілью є 11. Гравці мають
викинути 10 або менше, щоб перемогти - знову неважка ціль. Тепер, декілька
раундів пізніше, ціль зменшилась до 5. Тепер більше ніж половина кидків
буде перевершувати ціль, і, таким чином, не виграє. Тепер для перемоги
витрачається експоненціальна кількість кидків, з тим, як ціль зменшується.
З часом, коли ціль стає 2 (мінімальна з можливих), тільки один кидок з
кожних 36, або 2% з них, буде продукувати переможний результат.
З точки зору спостерігача, який знає, що ціллю гри є 2 якщо дехто буде
успішним, зробивши переможний кидок, він буде вважати, що той зробив в
середньому 36 кидків. Іншими словами, дехто може очікувати кількість
роботи, що потрібна для отримання успіху від складності, що закладена в
цілі. Коли алгоритм бізується на детерміністській функції, як SHA256,
самий вхід складає доказ, що було виконано певний обсяг роботи, щоб
спродукувати результат щодо цілі. Таким чином ми кажемо про доказ
виконаної роботи.
Навіть якщо б кожна спроба продукувала довільний результат, вірогідність
від можливих виходів могла б бути обчисленою заздалегідь. Таким чином,
вихід від очікуваної складності задовільняє підтвердженню вказаної
кількості виконаної роботи.
В Прикладі 10-10 виграшний "довісок" є 13, та цей результат може бути
підтвердженний будь-ким, незалежно. Будь-хто може додати суфікс в вигляді
числа 13 до фрази “I am Satoshi Nakamoto”, та обчислити хеш, та
перевірити, що він менший за ціль. Вдалий результат також є доказом
виконанної роботи, Proof-of-Work, оскільки він свідчить, що ми виконали
роботу щодо пошуку цього довіску. Доки він має тільки одне обчислення
хешу, це займе лише 13 обчислень хешу для пошуку працюючого довіску. Якщо
ми збільшимо складність, та зменшимо ціль, це займе більше обчислень хешу
для пошуку відповідного довіску, але тільки один хеш має бути
веріфікований кожним. Більше того, знаючи ціль, будь-хто може оцінити
складність, використовуючи статистику, і, таким чином, знати, скільки
роботи було потрібне для пошуку цього довіску.
Алгоритм Proof-of-Work має продукувати хеш, що меньший за ціль. Більша ціль означає меншу складність для пошуку хешу, що меньший цілі. нижча ціль означає, що буде більш складно знайти хеш, менший за ціль. Ціль ті складність пов'язані взаємно обратньо. Перевірка виконаної роботи в біткоін дуже подібна назмагання в Прикладі 10-10. Майнер збирає блок-кандидат, заповнений транзакціями. Далі майнер обчислює хеш заголовку блоку, та дивиться, чи він менший за встановлену ціль. Якщо хеш не меньший за ціль, майнер буде змінювати довісок (звичайно просто збільшуючи його на одщин), та пробуваит знову. За заданої складності в мережі біткоін, майнери мають перевірити квадрільйони разів, перед тим, як знайти довісок-нонс, що призведе до достатньо малого хешу заголовку блоку.
Дуже спрощений алгоритм Proof-of-Work, реалізований в Python, наданий в
Прикладі 10-11.
Приклад 10-11. Спрощена реалізація Proof-of-Work
#!/usr/bin/env python
# приклад алгоритму proof-of-work
import hashlib
import time
max_nonce = 2 ** 32 # 4 billion
def proof_of_work(header, difficulty_bits):
target = 2 ** (256-difficulty_bits) # обчислення цілі складності for nonce in xrange(max_nonce):
hash_result = hashlib.sha256(str(header)+str(nonce)).hexdigest()
if long(hash_result, 16) < target: # перевірка, ци це валідний результат, що меньше цілі print "Success with nonce %d" % nonce
print "Hash is %s" % hash_result
return (hash_result,nonce)
print "Failed after %d (max_nonce) tries" % nonce
return nonce
if __name__ == '__main__':
nonce = 0
hash_result = ''
for difficulty_bits in xrange(32): # складність від 0 до 31 біт difficulty = 2 ** difficulty_bits
print "\nDifficulty: %ld (%d bits)" % (difficulty, difficulty_bits)
print "Starting search..."
start_time = time.time() # поточний час # створюємо умовний блок, що включає хеш з попереднього блоку
new_block = 'test block with transactions' + hash_result
# find a valid nonce for the new block
(hash_result, nonce) = proof_of_work(new_block, difficulty_bits)
end_time = time.time() # обчислюємо час калькуляції elapsed_time = end_time - start_time
print "Elapsed Time: %.4f seconds" % elapsed_time
if elapsed_time > 0:
hash_power = float(long(nonce)/elapsed_time) # estimate the hashes per second print "Hashing Power: %ld hashes per second" % hash_power
Виконуючи цей код, ви можете встановити бажану складність (в бітах, скільки передніх бітів має бути нулями), та побачити, скільки це забирає в вашого комп'ютера, щоб обчислити це:
Приклад 10-12.Виконання прикладу Proof-of-Work для різних складностей
$ python proof-of-work-example.py*
Difficulty: 1 (0 bits)
[...]
Difficulty: 8 (3 bits)
Starting search...
Success with nonce 9
Hash is 1c1c105e65b47142f028a8f93ddf3dabb9260491bc64474738133ce5256cb3c1
Elapsed Time: 0.0004 seconds
Hashing Power: 25065 hashes per second
Difficulty: 16 (4 bits)
Starting search...
Success with nonce 25
Hash is 0f7becfd3bcd1a82e06663c97176add89e7cae0268de46f94e7e11bc3863e148
Elapsed Time: 0.0005 seconds
Hashing Power: 52507 hashes per second
Difficulty: 32 (5 bits)
Starting search...
Success with nonce 36
Hash is 029ae6e5004302a120630adcbb808452346ab1cf0b94c5189ba8bac1d47e7903
Elapsed Time: 0.0006 seconds
Hashing Power: 58164 hashes per second
[...]
Difficulty: 4194304 (22 bits)
Starting search...
Success with nonce 1759164
Hash is 0000008bb8f0e731f0496b8e530da984e85fb3cd2bd81882fe8ba3610b6cefc3
Elapsed Time: 13.3201 seconds
Hashing Power: 132068 hashes per second
Difficulty: 8388608 (23 bits)
Starting search...
Success with nonce 14214729
Hash is 000001408cf12dbd20fcba6372a223e098d58786c6ff93488a9f74f5df4df0a3
Elapsed Time: 110.1507 seconds
Hashing Power: 129048 hashes per second
Difficulty: 16777216 (24 bits)
Starting search...
Success with nonce 24586379
Hash is 0000002c3d6b370fccd699708d1b7cb4a94388595171366b944d68b2acce8b95
Elapsed Time: 195.2991 seconds
Hashing Power: 125890 hashes per second
[...]
Difficulty: 67108864 (26 bits)
Starting search...
Success with nonce 84561291
Hash is 0000001f0ea21e676b6dde5ad429b9d131a9f2b000802ab2f169cbca22b1e21a
Elapsed Time: 665.0949 seconds
Hashing Power: 127141 hashes per second
Як ви можете бачити, збільшення складності на 1 біт призводить до
подвоєння в часі, що потрібен для пошуку рішення. Якщо ви подумаєте про
цілий простір 256-бітних чисел, кожного разу, коли ви обмежуєте один біт
до нуля, ви зменшуєте простір пошуку навпіл. В Прикладі 10-12 потрібно 84
мільйони хеш спроб для пошуку довіска, що продукує хеш з 26 першими бітами
нулів. Навіть на швидкості більще ніж 120 000 хешів на секунду, все ще
треба 10 хвилин на лептопі для пошуку цього рішення.
На час написання мережа намагається знайти блок, хеш заголовка якого менший ніж:
0000000000000000029AB9000000000000000000000000000000000000000000
Як ви можете бачити, є багато нулів на початку цілі, що означає наш
диапазон хешів став значно менший, так що знайти валідний хеш стає значно
складнішим. Для мережі це вимагає в середньому більше ніж 1,8 септа-хешей
(тисяч мільярдів мільярдів хешей) на секунду, щоб знайти наступний блок.
Це виглядає як неможливе завдання, але на щастя мережа дає 3 екза-хешів на
секунду (EH/sec) обчислювальної потужності, що здатні знаходити блок в
середньому з 10 хвилин.
В Прикладі 10-3, ми бачили, що блок містить ціль в нотації, названою
“цільові біти”, або просто “біти”, що для блока 277 316 має значення
0x1903a30c. Ця нотація виражає ціль доказу виконанної роботи в форматі
коефіціент/експонента, де перші дві шістнадцятирічні цифри є експонентою,
та наступні шість цифер є коефіцієнтом. Таким чином в цьому блоці
експонента є 0x19, та коефіціент 0x03a30c.
Формула для обчислення цільової складності з цього представлення
наступна:
target = coefficient * 2^(8 * (exponent – 3))
Використовуючи цю формулу, та бітами складності 0x1903a30c, ми отримуємо:
target = 0x03a30c * 2^(0x08 * (0x19 - 0x03))^
=> target = 0x03a30c * 2^(0x08 * 0x16)^
=> target = 0x03a30c * 2^0xB0^
або в десятичній формі:
=> target = 238,348 * 2^176^
=> target =
22,829,202,948,393,929,850,749,706,076,701,368,331,072,452,018,388,575,715,328
перемикаючись знову до шістнадцятирічної форми:
=> target = 0x0000000000000003A30C00000000000000000000000000000000000000000000
Це означає, що валідний блок для висоти 277 316 є такий, у якого хеш заголовка менший за ціль. В бінарноми вигляді це число повинно мати більше ніж 60 перших нульових бітів. З цім рівнем складності поодинокий майнер, що обробляє 1 триліон хешів на секунду (1 терахеш на секунду, або 1 TH/sec), повинен знаходити рішення в середньому для одного блоку з 8496, або раз на 59 днів.
Як ми побачили, ціль визначає складність, і, таким чином, впливає на те, як довго треба шукати рішення для алгоритма доказу виконаної роботи. Це приводить до очевидного питання: чому треба підлаштовувати складність, хто її підлаштовує, та яким чином?
Блоки біткоін генеруються в середньому кожні 10 хвилин. Це пульс біткоіну, що фіксує частоту випуску валюти, а також швидкість закріплення транзакцій. Цей час має залишатись сталим, не тільки протягом короткого терміну, але також на періоді в декілька десятиріч. Очікується, що з часом потужність комп'ютерів буде зростати швидкими темпами. Щоб підтримувати час генерації блока в 10 хвилин, складність майнінгу має налаштовуватись, щоб приймати до уваги ці зміни. Фактично, ціль доказу виконаної роботи є динамічним параметром, що періодично підлаштовується, щоб відповідати 10-хвилинному виробництву блоків. Просто кажучи, ціль встановлюється таким чином, щоб нагальна обчислювальна потужність призводила до 10-хвилинного інтервалу блоків.
Тоді як робиться таке підлаштування в повнісью децентралізованій мережі?
Зміна цілі виконується автоматично, та незалежно на кожному вузлі. Кожні
2016 блоків всі вузли змінюють ціль для доказу виконаної роботи. Рівняння
для зміни цілі обчислює час, за який обчислені останні 2016 блоків, та
порівнює це з очікуваним часом в 20160 хвилин (2016 разів по бажаному
10-хвилинному інтервалу). Обчислюється відношення між дійсним проміжком
часу, та бажаним, та робиться відповідне корегування цілі (вниз або
догори). Просто кажучи, якщо мережа знаходить блоки швидше ніж кожні 10
хвилин, складність зростає (ціль зменшується). Якщо знаходження блоків
повільніше, ніж очікувалось, складність зменьшується (ціль зростає).
Рівняння може бути підсумоване таким чином:
Нова Ціль = Стара Ціль * (Дійсний час обчислення останніх 2016 блоків /
20160 хвилин)
Приклад 10-13 показує код, що використовується в клієнті Bitcoin Core.
Приклад 10-13. Зміна цілі для доказу виконаної роботи: CalculateNextWorkRequired() в pow.cpp
// Обмежуємо крок підлаштування
int64_t nActualTimespan = pindexLast->GetBlockTime() - nFirstBlockTime;
LogPrintf(" nActualTimespan = %d before bounds\n", nActualTimespan);
if (nActualTimespan < params.nPowTargetTimespan/4)
nActualTimespan = params.nPowTargetTimespan/4;
if (nActualTimespan > params.nPowTargetTimespan*4)
nActualTimespan = params.nPowTargetTimespan*4;
// Зміна цілі
const arith_uint256 bnPowLimit = UintToArith256(params.powLimit);
arith_uint256 bnNew;
arith_uint256 bnOld;
bnNew.SetCompact(pindexLast->nBits);
bnOld = bnNew;
bnNew *= nActualTimespan;
bnNew /= params.nPowTargetTimespan;
if (bnNew > bnPowLimit)
bnNew = bnPowLimit;
Хоча калібровка цілі відбувається кожні 2016 блоків, завдяки окремій
помилці в оригінальному клієнті Bitcoin Core, розрахунки базуються на
загальному часі попередніх 2015 блоків (не 2016, як це має бути), що
призводить до похибки зміни цілі на 0.05%. Параметри Interval (2016
блоків), та TargetTimespan (два тижні як 1209600 секунд), визначені в
chainparams.cpp.
Щоб запобігти надмірно волатильній складності (тобто, швидким перепадам, прим. перекл.), підлаштування має не перевищувати коефіціент чотири (4) за цикл. Якщо запитане підлаштування більше ніж в чотири рази, воне буде обмежене коефіціентом чотири, і не більше. Кожне наступне підлаштування буде досягнуте через наступний період зміни цілі, та дисбаланс буде зберігатись на протязі наступних 2016 блоків. Таким чином, довготривалі невідповідності між потужністю хешування, та складності, може зайняти декілька циклів в 2016 блоків, доки знову не буде досягнутий баланс.
Складність майнингу блоку біткоіну є приблизно 10 хвилин обробки для всієї мережі, базуючись на часі, що зайняв майнинг попередніх 2016 блоків, що підлаштовується кожні 2016 блоків. Це досягається через зниження або піднесення цілі.
Зауважте, що ціль незалежна від числа транзакцій, або вартості транзакцій. Це означає, що кількість потужності хешування, і, таким чином, витрат на електро енергію, витрачених на унебезпечення біткоінів, також повністю незалежні від числа транзакцій. Біткоін може маштабуватись, досягати більшого поширення, та залишатись безпечним, без жодного збільшення потужності хешування від сьогоднішнього рівня. Збільшення хешингової потужності представляє ринкові сили, по мірі того, як нові майнери виходять на ринок, щоб позмагатися за винагороду. Доки існує досить хешингової потужності, що контролюється часно граючими за винагороду майнерами, цього буде достатньо для атак типу "захвату", і, таким чином, досить для безпеки біткоіну.
Складність майнингу близько пов'язана з вартістю електрики та обмінного курсу біткоіна в термінах валюти, що використовує цю електричну енергію. Високопотужні системи майнингу намагаються бути такими ефективними, як це можливо, з сучасним поколінням виробництва кремнію, перетворюючи електрику в обчислення хешів, з найбільшою можливою потужністю. Первинний вплив не ринок майнингу є ціна однієї кіловат-години електрики в біткоіні, оскільки це визначає прибутковість майнингу, і, таким чином, стимулів для входу або виходу з ринку майнінгу.
Як ми бачили раніше, вузол Джинга побудував блок-кандидат, та підготував його для майнингу. Джинг має декілька апаратних стоєк для майнингу, насичений застосування-специфічними інтегрованими пристроями, де сотні та тисячі інтегрованих пристроїв виконуть алгоритм SHA256 паралельно з неймовірною швидкістю. Багато з ціх спеціалізованих машин під'єднані до свого майнингового вузла через USB або локальну мережу. Далі, майнинговий вузол, що виконується на десктопі Джинга, передає заголовок блоку до свого майнингового устаткування, що починає тестування трильйони довісків. Майже за 11 хвилин після початку майнингу блоку 277316, одна з апаратних майнингових машин знаходить рішення, та надсилає його назад, до майнингового вузла. Тоді, вставлене в заголовок блоку, довісок 924,591,752 продукує хеш блоку:
0000000000000001b6b9a13b095e96db41c4a928b97ef2d944a9b31b2cc7bdc4
і це є менше за ціль:
0000000000000003A30C00000000000000000000000000000000000000000000
Безвідкладно майнинговий вузол Джинга передає цей блок всім відомим йому сторонам. Вони приймають, перевіряють, та після цього просувають цей блок далі. З часом, коли цей блок заповнює всю мережу, кожний вузол додає його до власної копії блокчейну, розширюючи його до нової висоти в 277 316 блоків. По мірі того, як майнаючі блоки отримують та підтверджують новий блок, вони припиняють власні спроби знайти блок на тій же висоті, та безпосередньо починають обчислювати наступний блок в ланцюгові, використовуючи блок Джинга як "батьківській". Через будівницьтво на цьому новому блоці від Джинга, інші майнери, насправді, “голосують” власною потужністю майнинга, та схвалюють блок Джинга, та весь ланцюг, що він подовжує. В наступному розділі ми поглянемо на процес, що використовує кожний вузол для валідації блоку, та вибору найдовшого ланцюга, створюючи консенсус, що формує децентралізований блокчейн.
Третій крок в механізму консенсусу біткоіну є незалежна валідація кожного нового блоку кожним вузлом мережі. По мірі того, як новий вирішений блок просувається по мережі, кожний вузол виконує серію перевірок, щоб валідутувати його, перед тим, як просувати його відомим сторонам. Це надає переконання, що тільки валідні блоки курсують мережою. Незалежна валідація також гарантує, що майнери, які діють чесно, отримують свої біткоіни в блокчейні, і так отримують винагороду. Tі майнери, що діють безчесно, будуть мати свої блоки відхиленими, та не тільки втратять винагороду, але і також втратять вартість своїз спроб знайти рішення доказу виконаної роботи, таким чином втративши вартість електроенергії без компенсації.
When a node receives a new block, it will validate the block by checking
it against a
long list of criteria that must all be met; otherwise, the block is
rejected. These criteria
can be seen in the Bitcoin Core client in the functions CheckBlock and
CheckBlock
Header and include:
• The block data structure is syntactically valid
• The block header hash is less than the target (enforces the
Proof-of-Work)
• The block timestamp is less than two hours in the future (allowing for
time
errors)
• The block size is within acceptable limits
• The first transaction (and only the first) is a coinbase transaction
• All transactions within the block are valid using the transaction
checklist dis‐
cussed in “Independent Verification of Transactions” on page 218
The independent validation of each new block by every node on the network
ensures
that the miners cannot cheat. In previous sections we saw how miners get
to write a
transaction that awards them the new bitcoin created within the block and
claim the
transaction fees. Why don’t miners write themselves a transaction for a
thousand bit‐
coin instead of the correct reward? Because every node validates blocks
according to
the same rules. An invalid coinbase transaction would make the entire
block invalid,
which would result in the block being rejected and, therefore, that
transaction would
never become part of the ledger. The miners have to construct a perfect
block, based
on the shared rules that all nodes follow, and mine it with a correct
solution to the
Proof-of-Work. To do so, they expend a lot of electricity in mining, and
if they cheat,
all the electricity and effort is wasted. This is why independent
validation is a key
component of decentralized consensus.
The final step in bitcoin’s decentralized consensus mechanism is the
assembly of
blocks into chains and the selection of the chain with the most
Proof-of-Work. Once
a node has validated a new block, it will then attempt to assemble a chain
by connect‐
ing the block to the existing blockchain.
Nodes maintain three sets of blocks: those connected to the main
blockchain, those
that form branches off the main blockchain (secondary chains), and
finally, blocks
that do not have a known parent in the known chains (orphans). Invalid
blocks are
rejected as soon as any one of the validation criteria fails and are
therefore not
included in any chain.
The “main chain” at any time is whichever valid chain of blocks has the
most cumula‐
tive Proof-of-Work associated with it. Under most circumstances this is
also the chain
with the most blocks in it, unless there are two equal-length chains and
one has more
Proof-of-Work. The main chain will also have branches with blocks that are
“siblings”
to the blocks on the main chain. These blocks are valid but not part of
the main
chain. They are kept for future reference, in case one of those chains is
extended to
exceed the main chain in work. In the next section (“Blockchain Forks” on
page 240),
we will see how secondary chains occur as a result of an almost
simultaneous mining
of blocks at the same height.
When a new block is received, a node will try to slot it into the
existing blockchain.
The node will look at the block’s “previous block hash” field, which is
the reference to
the block’s parent. Then, the node will attempt to find that parent in the
existing
blockchain. Most of the time, the parent will be the “tip” of the main
chain, meaning
this new block extends the main chain. For example, the new block 277,316
has a ref‐
erence to the hash of its parent block 277,315. Most nodes that receive
277,316 will
already have block 277,315 as the tip of their main chain and will
therefore link the
new block and extend that chain.
Sometimes, as we will see in “Blockchain Forks” on page 240, the new
block extends a
chain that is not the main chain. In that case, the node will attach the
new block to
the secondary chain it extends and then compare the work of the secondary
chain to
the main chain. If the secondary chain has more cumulative work than the
https://www.google.com.ua/search?q=%D0%B7%D0%B4%D1%84%D0%BD&oq=%D0%B7%D0%B4%D1%84%D0%BD&aqs=chrome..69i57j0l5.1633j0j7&sourceid=chrome&ie=UTF-8main
chain, the node will reconverge on the secondary chain, meaning it will
select the sec‐
ondary chain as its new main chain, making the old main chain a secondary
chain. If
the node is a miner, it will now construct a block extending this new,
longer, chain.
If a valid block is received and no parent is found in the existing
chains, that block is
considered an “orphan.” Orphan blocks are saved in the orphan block pool
where
they will stay until their parent is received. Once the parent is received
and linked
into the existing chains, the orphan can be pulled out of the orphan pool
and linked
to the parent, making it part of a chain. Orphan blocks usually occur when
two
blocks that were mined within a short time of each other are received in
reverse order
(child before parent).
By selecting the greatest-cumulative-work valid chain, all nodes
eventually achieve
network-wide consensus. Temporary discrepancies between chains are
resolved even‐
tually as more work is added, extending one of the possible chains. Mining
nodes
“vote” with their mining power by choosing which chain to extend by mining
the
next block. When they mine a new block and extend the chain, the new block
itself
represents their vote.
In the next section we will look at how discrepancies between competing
chains
(forks) are resolved by the independent selection of the
greatest-cumulative-work
chain.
Because the blockchain is a decentralized data structure, different
copies of it are not
always consistent. Blocks might arrive at different nodes at different
times, causing
the nodes to have different perspectives of the blockchain. To resolve
this, each node
always selects and attempts to extend the chain of blocks that represents
the most
Proof-of-Work, also known as the longest chain or greatest cumulative work
chain.
By summing the work recorded in each block in a chain, a node can
calculhttps://www.google.com.ua/search?q=%D0%B7%D0%B4%D1%84%D0%BD&oq=%D0%B7%D0%B4%D1%84%D0%BD&aqs=chrome..69i57j0l5.1633j0j7&sourceid=chrome&ie=UTF-8ate
the
total amount of work that has been expended to create that chain. As long
as all nodes
select the greatest-cumulative-work chain, the global bitcoin network
eventually con‐
verges to a consistent state. Forks occur as temporary inconsistencies
between ver‐
sions of the blockchain, which are resolved by eventual reconvergence as
more blocks
are added to one of the forks.
The blockchain forks described in this section occur naturally as a
result of transmission delays in the global network. We will also
look at deliberately induced forks later in this chapter.
In the next few diagrams, we follow the progress of a “fork” event across
the network.
The diagram is a simplified representation of the bitcoin network. For
illustration
purposes, different blocks are shown as different shapes (star, triangle,
upside-down
triangle, rhombus), spreading across the network. Each node in the network
is repre‐
sented as a circle.
Each node has its own perspective of the global blockchain. As each node
receives
blocks from its neighbors, it updates its own copy of the blockchain,
selecting the
greatest-cumulative-work chain. For illustration purposes, each node
contains a
shape that represents the block that it believes is currently the tip of
the main chain.
So, if you see a star shape in the node, that means that the star block is
the tip of the
main chain, as far as that node is concerned.
In the first diagram (Малюнок 10-2), the network has a unified
perspective of the block‐
chain, with the star block as the tip of the main chain.
Малюнок 10-2. Before the fork—all nodes have the same perspective
A “fork” occurs whenever there are two candidate blocks competing to form
the
longest blockchain. This occurs under normal conditions whenever two
miners solve
the Proof-of-Work algorithm within a short period of time from each other.
As both
miners discover a solution for their respective candidate blocks, they
immediately
broadcast their own “winning” block to their immediate neighbors who begin
propa‐
gating the block across the network. Each node that receives a valid block
will incor‐
porate it into its blockchain, extending the blockchain by one block. If
that node later
sees another candidate block extending the same parent, it connects the
second can‐
didate on a secondary chain. As a result, some nodes will “see” one
candidate block
first, while other nodes will see the other candidate block and two
competing versions
of the blockchain will emerge.
In Малюнок 10-3, we see two miners (Node X and Node Y) who mine
two different
blocks almost simultaneously. Both of these blocks are children of the
star block, and
extend the chain by building on top of the star block. To help us track
it, one is visual‐
ized as a triangle block originating from Node X, and the other is shown
as an upside-
down triangle block originating from Node Y.
Малюнок 10-3. Visualization of a blockchain fork event: two blocks
found simultaneously
Let’s assume, for example, that a miner Node X finds a Proof-of-Work
solution for a
block “triangle” that extends the blockchain, building on top of the
parent block
“star.” Almost simultaneously, the miner Node Y who was also extending the
chain
from block “star” finds a solution for block “upside-down triangle,” his
candidate
block. Now, there are two possible blocks; one we call “triangle,”
originating in Node
X; and one we call “upside-down triangle,” originating in Node Y. Both
blocks are
valid, both blocks contain a valid solution to the Proof-of-Work, and both
blohttps://www.google.com.ua/search?q=%D0%B7%D0%B4%D1%84%D0%BD&oq=%D0%B7%D0%B4%D1%84%D0%BD&aqs=chrome..69i57j0l5.1633j0j7&sourceid=chrome&ie=UTF-8cks
extend the same parent (block “star”). Both blocks likely contain most of
the same
transactions, with only perhaps a few differences in the order of
transactions.
As the two blocks propagate, some nodes receive block “triangle” first and
some
receive block “upside-down triangle” first. As shown in Малюнок
10-4, the network
splits into two different perspectives of the blockchain; one side topped
with a trian‐
gle block, the other with the upside-down-triangle block.
Малюнок 10-4. Visualization of a blockchain fork event: two blocks
propagate, splitting the
network
In the diagram, a randomly chosen “Node X” received the triangle block
first and
extended the star chain with it. Node X selected the chain with “triangle”
block as the
main chain. Later, Node X also received the “upside-down triangle” block.
Since it
was received second, it is assumed to have “lost” the race. Yet, the
“upside-down triangle” block is not discarded. It is linked to the “star”
block parent and forms a secondary chain. While Node X assumes it has
correctly selected the winning chain, it
keeps the “losing” chain so that it has the information needed to
reconverge if the
“losing” chain ends up
“winning.”https://www.google.com.ua/search?q=%D0%B7%D0%B4%D1%84%D0%BD&oq=%D0%B7%D0%B4%D1%84%D0%BD&aqs=chrome..69i57j0l5.1633j0j7&sourceid=chrome&ie=UTF-8
On the other side of the network, Node Y constructs a blockchain based
on its own
perspective of the sequence of events. It received “upside-down triangle”
first and
elected that chain as the “winner.” When it later received “triangle”
block, it connec‐
ted it to the “star” block parent as a secondary chain.
Neither side is “correct,” or “incorrect.” Both are valid perspectives
of the blockchain.
Only in hindsight will one prevail, based on how these two competing
chains are
extended by additional work.
Mining nodes whose perspective resembles Node X will immediately begin
mining a
candidate block that extends the chain with “triangle” as its tip. By
linking “triangle”
as the parent of their candidate block, they are voting with their hashing
power. Their
vote supports the chain that they have elected as the main chain.
Any mining node whose perspective resembles Node Y will start building a
candidate
node with “upside-down triangle” as its parent, extending the chain that
they believe
is the main chain. And so, the race begins again.
Forks are almost always resolved within one block. While part of the
network’s hash‐
ing power is dedicated to building on top of “triangle” as the parent,
another part of
the hashing power is focused on building on top of “upside-down triangle.”
Even if
the hashing power is almost evenly split, it is likely that one set of
miners will find a
solution and propagate it before the other set of miners have found any
solutions.
Let’s say, for example, that the miners building on top of “triangle” find
a new block
“rhombus” that extends the chain (e.g., star-triangle-rhombus). They
immediately
propagate this new block and the entire network sees it as a valid
solution as shown
in Малюнок 10-5.
All nodes that had chosen “triangle” as the winner in the previous round
will simply
extend the chain one more block. The nodes that chose “upside-down
triangle” as the
winner, however, will now see two chains: star-triangle-rhombus and
star-upside-
down-triangle. The chain star-triangle-rhombus is now longer (more
cumulative
work) than the other chain. As a result, those nodes will set the chain
star-triangle-
rhombus as the main chain and change the star-upside-down-triangle chain
to a sec‐
ondary chain, as shown in Малюнок 10-6. This is a chain
reconvergence, because those
nodes are forced to revise their view of the blockchain to incorporate the
new evi‐
dence of a longer chain. Any miners working on extending the chain
star-upside-
down-triangle will now stop that work because their candidate block is an
“orphan,”
as its parent “upside-down-triangle” is no longer on the longest chain.
The transac‐
tions within “upside-down-triangle” are re-inserted in the mempool for
inclusion in the next block, because the block they were in is no longer
in the main chain. The entire network reconverges on a single blockchain
star-triangle-rhombus, with
“rhombus” as the last block in the chain. All miners immediately start
working on
candidate blocks that reference “rhombus” as their parent to extend the
star-triangle-
rhombus chain.
Малюнок 10-5. Visualization of a blockchain fork event: a new block
extends one fork,
reconverging the network
Малюнок 10-6. Visualization of a blockchain fork event: the network
reconverges on a new
longest chain
It is theoretically possible for a fork to extend to two blocks, if two
blocks are found
almost simultaneously by miners on opposite “sides” of a previous fork.
However, the
chance of that happening is very low. Whereas a one-block fork might occur
every
day, a two-block fork occurs at most once every few weeks.
Bitcoin’s block interval of 10 minutes is a design compromise between
fast confirma‐
tion times (settlement of transactions) and the probability of a fork. A
faster block
time would make transactions clear faster but lead to more frequent
blockchain forks,
whereas a slower block time would decrease the number of forks but make
settlement
slower.
Bitcoin mining is an extremely competitive industry. The hashing power
has
increased exponentially every year of bitcoin’s existence. Some years the
growth has
reflected a complete change of technology, such as in 2010 and 2011 when
many min‐
ers switched from using CPU mining to GPU mining and field programmable
gate
array (FPGA) mining. In 2013 the introduction of ASIC mining lead to
another giant
leap in mining power, by placing the SHA256 function directly on silicon
chips speci‐
alized for the purpose of mining. The first such chips could deliver more
mining
power in a single box than the entire bitcoin network in 2010.
The following list shows the total hashing power of the bitcoin network,
over the first
eight years of operation:
2009
0.5 MH/sec–8 MH/sec (16× growth)
2010
8 MH/sec–116 GH/sec (14,500× growth)
2011
16 GH/sec–9 TH/sec (562× growth)
2012
9 TH/sec–23 TH/sec (2.5× growth)
2013
23 TH/sec–10 PH/sec (450× growth)
2014
10 PH/sec–300 PH/sec (3000× growth)
2015
300 PH/sec-800 PH/sec (266× growth)
2016
800 PH/sec-2.5 EH/sec (312× growth))
In the chart in Малюнок 10-7, we can see that bitcoin network’s
hashing power increased
over the past two years. As you can see, the competition between miners
and the growth of bitcoin has resulted in an exponential increase in the
hashing power (total
hashes per second across the network).
Малюнок 10-7. Total hashing power, terahashes per second (TH/sec)
As the amount of hashing power applied to mining bitcoin has exploded,
the diffi‐
culty has risen to match it. The difficulty metric in the chart shown in
Малюнок 10-8 is
measured as a ratio of current difficulty over minimum difficulty (the
difficulty of the
first block).
Малюнок 10-8. Bitcoin’s mining difficulty metric
In the last two years, the ASIC mining chips have become increasingly
denser,
approaching the cutting edge of silicon fabrication with a feature size
(resolution) of
16 nanometers (nm). Currently, ASIC manufacturers are aiming to overtake
general-
purpose CPU chip manufacturers, designing chips with a feature size of 14
nm,
because the profitability of mining is driving this industry even faster
than general
computing. There are no more giant leaps left in bitcoin mining, because
the industry
has reached the forefront of Moore’s Law, which stipulates that computing
density
will double approximately every 18 months. Still, the mining power of the
network
continues to advance at an exponential pace as the race for higher density
chips is
matched with a race for higher density data centers where thousands of
these chips
can be deployed. It’s no longer about how much mining can be done with one
chip,
but how many chips can be squeezed into a building, while still
dissipating the heat
and providing adequate power.
Since 2012, bitcoin mining has evolved to resolve a fundamental
limitation in the
structure of the block header. In the early days of bitcoin, a miner could
find a block
by iterating through the nonce until the resulting hash was below the
target. As diffi‐
culty increased, miners often cycled through all 4 billion values of the
nonce without
finding a block. However, this was easily resolved by updating the block
timestamp to
account for the elapsed time. Because the timestamp is part of the header,
the change
would allow miners to iterate through the values of the nonce again with
different
results. Once mining hardware exceeded 4 GH/sec, however, this approach
became
increasingly difficult because the nonce values were exhausted in less
than a second.
As ASIC mining equipment started pushing and then exceeding the TH/sec
hash
rate, the mining software needed more space for nonce values in order to
find valid
blocks. The timestamp could be stretched a bit, but moving it too far into
the future
would cause the block to become invalid. A new source of “change” was
needed in the
block header. The solution was to use the coinbase transaction as a source
of extra
nonce values. Because the coinbase script can store between 2 and 100
bytes of data,
miners started using that space as extra nonce space, allowing them to
explore a
much larger range of block header values to find valid blocks. The
coinbase transac‐
tion is included in the merkle tree, which means that any change in the
coinbase
script causes the merkle root to change. Eight bytes of extra nonce, plus
the 4 bytes of
“standard” nonce allow miners to explore a total 296 (8 followed by 28
zeros) possibili‐
ties per second without having to modify the timestamp. If, in the future,
miners
could run through all these possibilities, they could then modify the
timestamp.
There is also more space in the coinbase script for future expansion of
the extra
nonce space.
Successful blocks pay the reward to a pool bitcoin address, rather than
individual
miners. The pool server will periodically make payments to the miners’
bitcoin
addresses, once their share of the rewards has reached a certain
threshold. Typically,
the pool server charges a percentage fee of the rewards for providing the
pool-mining
service.
Miners participating in a pool split the work of searching for a
solution to a candidate
block, earning “shares” for their mining contribution. The mining pool
sets a higher
target (lower difficulty) for earning a share, typically more than 1,000
times easier
than the bitcoin network’s target. When someone in the pool successfully
mines a
block, the reward is earned by the pool and then shared with all miners in
proportion
to the number of shares they contributed to the effort.
Pools are open to any miner, big or small, professional or amateur. A
pool will there‐
fore have some participants with a single small mining machine, and others
with a
garage full of high-end mining hardware. Some will be mining with a few
tens of a
kilowatt of electricity, others will be running a data center consuming a
megawatt of
power. How does a mining pool measure the individual contributions, so as
to fairly
distribute the rewards, without the possibility of cheating? The answer is
to use bit‐
coin’s Proof-of-Work algorithm to measure each pool miner’s contribution,
but set at
a lower difficulty so that even the smallest pool miners win a share
frequently enough
to make it worthwhile to contribute to the pool. By setting a lower
difficulty for earn‐
ing shares, the pool measures the amount of work done by each miner. Each
time a
pool miner finds a block header hash that is less than the pool target,
she proves she
has done the hashing work to find that result. More importantly, the work
to find
shares contributes, in a statistically measurable way, to the overall
effort to find a hash
lower than the bitcoin network’s target. Thousands of miners trying to
find low-value
hashes will eventually find one low enough to satisfy the bitcoin network
target.
Let’s return to the analogy of a dice game. If the dice players are
throwing dice with a
goal of throwing less than four (the overall network difficulty), a pool
would set an
easier target, counting how many times the pool players managed to throw
less than
eight. When pool players throw less than eight (the pool share target),
they earn
shares, but they don’t win the game because they don’t achieve the game
target (less
than four). The pool players will achieve the easier pool target much more
often,
earning them shares very regularly, even when they don’t achieve the
harder target of
winning the game. Every now and then, one of the pool players will throw
ahttps://www.google.com.ua/search?q=%D0%B7%D0%B4%D1%84%D0%BD&oq=%D0%B7%D0%B4%D1%84%D0%BD&aqs=chrome..69i57j0l5.1633j0j7&sourceid=chrome&ie=UTF-8
com‐
bined dice throw of less than four and the pool wins. Then, the earnings
can be dis‐
tributed to the pool players based on the shares they earned. Even though
the target
of eight-or-less wasn’t winning, it was a fair way to measure dice throws
for the play‐
ers, and it occasionally produces a less-than-four throw.
Similarly, a mining pool will set a (higher and easier) pool target that
will ensure that
an individual pool miner can find block header hashes that are less than
the pool tarold blocks practically immutable. Consensus attacks also do
not affect the security of the private keys and signing algorithm (ECDSA).
A consensus attack cannot steal bit‐
coin, spend bitcoin without signatures, redirect bitcoin, or otherwise
change past
transactions or ownership records. Consensus attacks can only affect the
most recent
blocks and cause denial-of-service disruptions on the creation of future
blocks.
One attack scenario against the consensus mechanism is called the “51%
attack.” In
this scenario a group of miners, controlling a majority (51%) of the total
network’s
hashing power, collude to attack bitcoin. With the ability to mine the
majorihttps://www.google.com.ua/search?q=%D0%B7%D0%B4%D1%84%D0%BD&oq=%D0%B7%D0%B4%D1%84%D0%BD&aqs=chrome..69i57j0l5.1633j0j7&sourceid=chrome&ie=UTF-8ty
of the
blocks, the attacking miners can cause deliberate “forks” in the
blockchain and
double-spend transactions or execute denial-of-service attacks against
spechttps://www.google.com.ua/search?q=%D0%B7%D0%B4%D1%84%D0%BD&oq=%D0%B7%D0%B4%D1%84%D0%BD&aqs=chrome..69i57j0l5.1633j0j7&sourceid=chrome&ie=UTF-8ific
trans‐
actions or addresses. A fork/double-spend attack is where the attacker
causes previ‐
ously confirmed blocks to be invalidated by forking below them and
re-convhttps://www.google.com.ua/search?q=%D0%B7%D0%B4%D1%84%D0%BD&oq=%D0%B7%D0%B4%D1%84%D0%BD&aqs=chrome..69i57j0l5.1633j0j7&sourceid=chrome&ie=UTF-8erging
on an alternate chain. With sufficient power, an attacker can invalidate
six or more
blocks in a row, causing transactions that were considered immutable (six
chttps://www.google.com.ua/search?q=%D0%B7%D0%B4%D1%84%D0%BD&oq=%D0%B7%D0%B4%D1%84%D0%BD&aqs=chrome..69i57j0l5.1633j0j7&sourceid=chrome&ie=UTF-8onfirma‐
tions) to be invalidated. Note that a double-spend can only be done on the
attacker’s
own transactions, for which the attacker can produce a valid signature.
Dohttps://www.google.com.ua/search?q=%D0%B7%D0%B4%D1%84%D0%BD&oq=%D0%B7%D0%B4%D1%84%D0%BD&aqs=chrome..69i57j0l5.1633j0j7&sourceid=chrome&ie=UTF-8uble-
spending one’s own transactions is profitable if by invalidating a
transaction the
attacker can get an irreversible exchange payment or product without
paying for it.
Let’s examine a practical example of a 51% attack. In the first chapter,
we looked at a
transaction between Alice and Bob for a cup of coffee. Bob, the cafe
owner, is willing
to accept payment for cups of coffee without waiting for confirmation
(minihttps://www.google.com.ua/search?q=%D0%B7%D0%B4%D1%84%D0%BD&oq=%D0%B7%D0%B4%D1%84%D0%BD&aqs=chrome..69i57j0l5.1633j0j7&sourceid=chrome&ie=UTF-8https://www.google.com.ua/search?q=%D0%B7%D0%B4%D1%84%D0%BD&oq=%D0%B7%D0%B4%D1%84%D0%BD&aqs=chrome..69i57j0l5.1633j0j7&sourceid=chrome&ie=UTF-8ng
in a
block), because the risk of a double-spend on a cup of coffee is low in
comparison to
the convenience of rapid customer service. This is similar to the practice
of coffee
shops that accept credit card payments without a signature for amounts
below $25,
because the risk of a credit-card chargeback is low while the cost of
delayinhttps://www.google.com.ua/search?q=%D0%B7%D0%B4%D1%84%D0%BD&oq=%D0%B7%D0%B4%D1%84%D0%BD&aqs=chrome..69i57j0l5.1633j0j7&sourceid=chrome&ie=UTF-8g
the
transaction to obtain a signature is comparatively larger. In contrast,
selling a more
expensive item for bitcoin runs the risk of a double-spend attack, where
the buyer
broadcasts a competing transaction that spends the same inputs (UTXO) and
cancels
the payment to the merchant. A double-spend attack can happen in two ways:
either
before a transaction is confirmed, or if the attacker takes advantage of a
blockchain
fork to undo several blocks. A 51% attack allows attackers to double-spend
their own
transactions in the new chain, thus undoing the corresponding transaction
in the old
chain.
In our example, malicious attacker Mallory goes to Carol’s gallery and
purchases a
beautiful triptych painting depicting Satoshi Nakamoto as Prometheus.
Carol sells
“The Great Fire” paintings for $250,000 in bitcoin to Mallory. Instead of
waiting for
six or more confirmations on the transaction, Carol wraps and hands the
paintings to
Mallory after only one confirmation. Mallory works with an accomplice,
Paul, who
operates a large mining pool, and the accomplice launches a 51% attack as
soon as
Mallory’s transaction is included in a block. Paul directs the mining pool
to remine
the same block height as the block containing Mallory’s transaction,
replacing Mallory’s payment to Carol with a transaction that double-spends
the same input as Mallory’s payment. The double-spend transaction consumes
the same UTXO and pays it
back to Mallory’s wallet, instead of paying it to Carol, essentially
allowing Mallory to
keep the bitcoin. Paul then directs the mining pool to mine an additional
block, so as
to make the chain containing the double-spend transaction longer than the
original
chain (causing a fork below the block containing Mallory’s transaction).
When the
blockchain fork resolves in favor of the new (longer) chain, the
double-spent transac‐
tion replaces the original payment to Carol. Carol is now missing the
three paintings
and also has no bitcoin payment. Throughout all this activity, Paul’s
mining pool par‐
ticipants might remain blissfully unaware of the double-spend attempt,
because they
mine with automated miners and cannot monitor every transaction or block.
To protect against this kind of attack, a merchant selling large-value
items must wait
at least six confirmations before giving the product to the buyer.
Alternatively, the
merchant should use an escrow multisignature account, again waiting for
several
confirmations after the escrow account is funded. The more confirmations
elapse, the
harder it becomes to invalidate a transaction with a 51% attack. For
high-value items,
payment by bitcoin will still be convenient and efficient even if the
buyer has to wait
24 hours for delivery, which would correspond to approximately 144
confirmhttps://www.google.com.ua/search?q=%D0%B7%D0%B4%D1%84%D0%BD&oq=%D0%B7%D0%B4%D1%84%D0%BD&aqs=chrome..69i57j0l5.1633j0j7&sourceid=chrome&ie=UTF-8ations.
In addition to a double-spend attack, the other scenario for a consensus
attack is to
deny service to specific bitcoin participants (specific bitcoin
addresses). An attacker
with a majority of the mining power can simply ignore specific
transactions. If they
are included in a block mined by another miner, the attacker can
deliberately fork
and remine that block, again excluding the specific transactions. This
type of attack
can result in a sustained denial-of-service against a specific address or
set of addresses
for as long as the attacker controls the majority of the mining power.
Despite its name, the 51% attack scenario doesn’t actually require 51% of
the hashing
power. In fact, such an attack can be attempted with a smaller percentage
of the hash‐
ing power. The 51% threshold is simply the level at which such an attack
is almost
guaranteed to succeed. A consensus attack is essentially a tug-of-war for
the next
block and the “stronger” group is more likely to win. With less hashing
power, the
probability of success is reduced, because other miners control the
generation of
some blocks with their “honest” mining power. One way to look at it is
that
thhttps://www.google.com.ua/search?q=%D0%B7%D0%B4%D1%84%D0%BD&oq=%D0%B7%D0%B4%D1%84%D0%BD&aqs=chrome..69i57j0l5.1633j0j7&sourceid=chrome&ie=UTF-8https://www.google.com.ua/search?q=%D0%B7%D0%B4%D1%84%D0%BD&oq=%D0%B7%D0%B4%D1%84%D0%BD&aqs=chrome..69i57j0l5.1633j0j7&sourceid=chrome&ie=UTF-8e
more
hashing power an attacker has, the longer the fork he can deliberately
create, the
more blocks in the recent past he can invalidate, or the more blocks in
the future he
can control. Security research groups have used statistical modeling to
claim that var‐
ious types of consensus attacks are possible with as little as 30% of the
hashing power.
The massive increase of total hashing power has arguably made bitcoin
impervious to
attacks by a single miner. There is no possible way for a solo miner to
control more
than a small percentage of the total mining power. However, the
centralization of
control caused by mining pools has introduced the risk of for-profit
attacks by a mining pool operator. The pool operator in a managed pool
controls the construction of candidate blocks and also controls which
transactions are included. This gives the
pool operator the power to exclude transactions or introduce double-spend
transac‐
tions. If such abuse of power is done in a limited and subtle way, a pool
operator
could conceivably profit from a consensus attack without being noticed.
Not all attackers will be motivated by profit, however. One potential
attack
schttps://www.google.com.ua/search?q=%D0%B7%D0%B4%D1%84%D0%BD&oq=%D0%B7%D0%B4%D1%84%D0%BD&aqs=chrome..69i57j0l5.1633j0j7&sourceid=chrome&ie=UTF-8enario
is
where an attacker intends to disrupt the bitcoin network without the
possibility of
profiting from such disruption. A malicious attack aimed at crippling
bitcoin would
require enormous investment and covert planning, but could conceivably be
launched by a well-funded, most likely state-sponsored, attacker.
Alternatively, a well-
funded attacker could attack bitcoin’s consensus by simultaneously
amassing mining
hardware, compromising pool operators, and attacking other pools with
denihttps://www.google.com.ua/search?q=%D0%B7%D0%B4%D1%84%D0%BD&oq=%D0%B7%D0%B4%D1%84%D0%BD&aqs=chrome..69i57j0l5.1633j0j7&sourceid=chrome&ie=UTF-8al-of-
service. All of these scenarios are theoretically possible, but
increasingly impractical
as the bitcoin network’s overall hashing power continues to grow
exponentially.
Undoubtedly, a serious consensus attack would erode confidence in bitcoin
in the
short term, possibly causing a significant price decline. However, the
bitcoin network
and software are constantly evolving, so consensus attacks would be met
with imme‐
diate countermeasures by the bitcoin community, making bitcoin hardier,
stealthier,
and more robust than ever.
The rules of consensus determine the validity of transactions and
blocks. These rules
are the basis for collaboration between all bitcoin nodes and are
responsible for the
convergence of all local perspectives into a single consistent blockchain
across the
entire network.
While the consensus rules are invariable in the short term and must be
consistent
across all nodes, they are not invariable in the long term. In order to
evolve and
develop the bitcoin system, the rules have to change from time to time to
accommo‐
date new features, improvements, or bug fixes. Unlike traditional software
develop‐
ment, however, upgrades to a consensus system are much more difficult and
require
coordination between all the participants.
Hard Forks
In “Blockchain Forks” on page 240 we looked at how the bitcoin network may
briefly
diverge, with two parts of the network following two different branches of
the block‐
chain for a short time. We saw how this process occurs naturally, as part
of the nor‐
mal operation of the network and how the network reconverges on a common
blockchain after one or more blocks are mined.
There is another scenario in which the network may diverge into following
two
chains: a change in the consensus rules. This type of fork is called a
hard fork, because
after the fork the network does not reconverge onto a single chain.
Instead, the two
chains evolve independently. Hard forks occur when part of the network is
operating
under a different set of consensus rules than the rest of the network.
This may occur
because of a bug or because of a deliberate change in the implementation
of the con‐
sensus rules.
Hard forks can be used to change the rules of consensus, but they
require coordina‐
tion between all participants in the system. Any nodes that do not upgrade
to the new
consensus rules are unable to participate in the consensus mechanism and
are forced
onto a separate chain at the moment of the hard fork. Thus, a change
introduced by a
hard fork can be thought of as not “forward compatible,” in that
nonupgraded sys‐
tems can no longer process the new consensus rules.
Let’s examine the mechanics of a hard fork with a specific example.
Малюнок 10-9 shows a blockchain with two forks. At block height 4, a
one-block fork
occurs. This is the type of spontaneous fork we saw in “Blockchain Forks”
on page
240. With the mining of block 5, the network reconverges on one chain and
the fork
is resolved.
Малюнок 10-9. A blockchain with forks
Later, however, at block height 6, a hard fork occurs. Let’s assume that
a new imple‐
mentation of the client is released with a change in the consensus rules.
Starting on
block height 7, miners running this new implementation will accept a new
type of
digital signature, let’s call it a “Smores” signature, that is not ECDSA
based. Immedi‐
ately after, a node running the new implementation creates a transaction
that contains
a Smores signature and a miner with the updated software mines block 7b
containing
this transaction.
Any node or miner that has not upgraded the software to validate Smores
signatures
is now unable to process block 7b. From their perspective, both the
transaction that
contained a Smores signature and block 7b that contained that transaction
are inva‐
lid, because they are evaluating them based upon the old consensus rules.
These
nodes will reject the transaction and the block and will not propagate
them. Any min‐
ers that are using the old rules will not accept block 7b and will
continue to mine a candidate block whose parent is block 6. In fact,
miners using the old rules may not even receive block 7b if all the nodes
they are connected to are also obeying the old
rules and therefore not propagating the block. Eventually, they will be
able to mine
block 7a, which is valid under the old rules and does not contain any
transactions
with Smores signatures.
The two chains continue to diverge from this point. Miners on the “b”
chain will con‐
tinue to accept and mine transactions containing Smores signatures, while
miners on
the “a” chain will continue to ignore these transactions. Even if block 8b
does not con‐
tain any Smores-signed transactions, the miners on the “a” chain cannot
process it. To
them it appears to be an orphan block, as its parent “7b” is not
recognized as a valid
block.
For software developers, the term “fork” has another meaning, adding
confusion to
the term “hard fork.” In open source software, a fork occurs when a group
of develop‐
ers choose to follow a different software roadmap and start a competing
implementa‐
tion of an open source project. We’ve already discussed two circumstances
that will
lead to a hard fork: a bug in the consensus rules and a deliberate
modification of the
consensus rules. In the case of a deliberate change to the consensus
rules, a software
fork precedes the hard fork. However, for this type of hard fork to occur,
a new soft‐
ware implementation of the consensus rules must be developed, adopted, and
launched.
Examples of software forks that have attempted to change consensus rules
include
Bitcoin XT, Bitcoin Classic, and most recently Bitcoin Unlimited. However,
none of
these software forks have resulted in a hard fork. While a software fork
is a necessary
precondition, it is not in itself sufficient for a hard fork to occur. For
a hard fork to
occur, the competing implementation must be adopted and the new rules
activated,
by miners, wallets, and intermediary nodes. Conversely, there are numerous
alterna‐
tive implementations of Bitcoin Core, and even software forks, that do not
change the
consensus rules and barring a bug, can coexist on the network and
interoperate
without causing a hard fork.
Consensus rules may differ in obvious and explicit ways, in the validation
of transac‐
tions or blocks. The rules may also differ in more subtle ways, in the
implementation
of the consensus rules as they apply to bitcoin scripts or cryptographic
primitives
such as digital signatures. Finally, the consensus rules may differ in
unanticipated
ways because of implicit consensus constraints imposed by system
limitations or
implementation details. An example of the latter was seen in the
unanticipated hard
fork during the upgrade of Bitcoin Core 0.7 to 0.8, which was caused by a
limitation
in the Berkley DB implementation used to store blocks.
Conceptually, we can think of a hard fork as developing in four stages:
a software
fork, a network fork, a mining fork, and a chain fork.
The process begins when an alternative implementation of the client, with
modified
consensus rules, is created by developers.
When this forked implementation is deployed in the network, a certain
percentage of
miners, wallet users, and intermediate nodes may adopt and run this
implementation.
A resulting fork will depend upon whether the new consensus rules apply to
blocks,
transactions, or some other aspect of the system. If the new consensus
rules pertain to
transactions, then a wallet creating a transaction under the new rules may
precipitate
a network fork, followed by a hard fork when the transaction is mined into
a block. If
the new rules pertain to blocks, then the hard fork process will begin
when a block is
mined under the new rules.
First, the network will fork. Nodes based on the original implementation
of the con‐
sensus rules will reject any transactions and blocks that are created
under the new
rules. Furthermore, the nodes following the original consensus rules will
temporarily
ban and disconnect from any nodes that are sending them these invalid
transactions
and blocks. As a result, the network will partition into two: old nodes
will only
remain connected to old nodes and new nodes will only be connected to new
nodes.
A single transaction or block based on the new rules will ripple through
the network
and result in the partition into two networks.
Once a miner using the new rules mines a block, the mining power and chain
will
also fork. New miners will mine on top of the new block, while old miners
will mine a
separate chain based on the old rules. The partitioned network will make
it so that the
miners operating on separate consensus rules won’t likely receive each
other’s blocks,
as they are connected to two separate networks.
As miners diverge into mining two different chains, the hashing power is
split
between the chains. The mining power can be split in any proportion
between the
two chains. The new rules may only be followed by a minority, or by the
vast majority
of the mining power.
Let’s assume, for example, an 80%–20% split, with the majority of the
mining power
using the new consensus rules. Let’s also assume that the fork occurs
immediately
after a retargeting period.
The two chains would each inherit the difficulty from the retargeting
period. The new
consensus rules would have 80% of the previously available mining power
committed
to them. From the perspective of this chain, the mining power has suddenly
declined
by 20% vis-a-vis the previous period. Blocks will be found on average
every 12
minutes, representing the 20% decline in mining power available to extend
this chain.
This rate of block issuance will continue (barring any changes in hashing
power) until
2016 blocks are mined, which will take approximately 24,192 minutes (at 12
minutes
per block), or 16.8 days. After 16.8 days, a retarget will occur and the
difficulty will
adjust (reduced by 20%) to produce 10-minute blocks again, based on the
reduced
amount of hashing power in this chain.
The minority chain, mining under the old rules with only 20% of the
hashing power,
will face a much more difficult task. On this chain, blocks will now be
mined every 50
minutes on average. The difficulty will not be adjusted for 2016 blocks,
which will
take 100,800 minutes, or approximately 10 weeks to mine. Assuming a fixed
capacity
per block, this will also result in a reduction of transaction capacity by
a factor of 5, as
there are fewer blocks per hour available to record transactions.
This is the dawn of consensus software development. Just as open source
develop‐
ment changed both the methods and products of software and created new
method‐
ologies, new tools, and new communities in its wake, consensus software
development also represents a new frontier in computer science. Out of the
debates,
experiments, and tribulations of the bitcoin development roadmap, we will
see new
development tools, practices, methodologies, and communities emerge.
Hard forks are seen as risky because they force a minority to either
upgrade or
remain on a minority chain. The risk of splitting the entire system into
two compet‐
ing systems is seen by many as an unacceptable risk. As a result, many
developers are
reluctant to use the hard fork mechanism to implement upgrades to the
consensus
rules, unless there is near-unanimous support from the entire network. Any
hard fork
proposals that do not have near-unanimous support are considered too
“contentious”
to attempt without risking a partition of the system.
The issue of hard forks is highly controversial in the bitcoin development
commu‐
nity, especially as it relates to any proposed changes to the consensus
rules controlling
the maximum block size limit. Some developers are opposed to any form of
hard
fork, seeing it as too risky. Others see the mechanism of hard fork as an
essential tool
for upgrading the consensus rules in a way that avoids “technical debt”
and provides a
clean break with the past. Finally, some developers see hard forks as a
mechanism
that should be used rarely, with a lot of advance planning and only under
near-
unanimous consensus.
Already we have seen the emergence of new methodologies to address the
risks of
hard forks. In the next section, we will look at soft forks, and the
BIP-34 and BIP-9
methods for signaling and activation of consensus modifications.
Not all consensus rule changes cause a hard fork. Only consensus changes
that are
forward-incompatible cause a fork. If the change is implemented in such a
way that
an unmodified client still sees the transaction or block as valid under
the previous
rules, the change can happen without a fork.
The term soft fork was introduced to distinguish this upgrade method
from a “hard
fork.” In practice, a soft fork is not a fork at all. A soft fork is a
forward-compatible
change to the consensus rules that allows unupgraded clients to continue
to operate
in consensus with the new rules.
One aspect of soft forks that is not immediately obvious is that soft
fork upgrades can
only be used to constrain the consensus rules, not to expand them. In
order to be for‐
ward compatible, transactions and blocks created under the new rules must
be valid
under the old rules too, but not vice versa. The new rules can only limit
what is valid;
otherwise, they will trigger a hard fork when rejected under the old
rules.
Soft forks can be implemented in a number of ways—the term does not define
a sin‐
gle method, rather a set of methods that all have one thing in common:
they don’t
require all nodes to upgrade or force nonupgraded nodes out of consensus.
A number of soft forks have been implemented in bitcoin, based on the
re-
interpretation of NOP opcodes. Bitcoin Script had ten opcodes reserved for
future
use, NOP1 through NOP10. Under the consensus rules, the presence of these
opcodes in a script is interpreted as a null-potent operator, meaning they
have no
effect. Execution continues after the NOP opcode as if it wasn’t there.
A soft fork therefore can modify the semantics of a NOP code to give it
new meaning.
For example, BIP-65 (CHECKLOCKTIMEVERIFY) reinterpreted the NOP2 opcode.
Clients
implementing BIP-65 interpret NOP2 as OP_CHECKLOCKTIMEVERIFY and impose an
absolute locktime consensus rule on UTXO that contain this opcode in their
locking
scripts. This change is a soft fork because a transaction that is valid
under BIP-65 is
also valid on any client that is not implementing (ignorant of) BIP-65. To
the old cli‐
ents, the script contains an NOP code, which is ignored.
The reinterpretation of NOP opcodes was both planned for and an obvious
mecha‐
nism for consensus upgrades. Recently, however, another soft fork
mechanism was
introduced that does not rely on NOP opcodes for a very specific type of
consensus
change. This is examined in more detail in Appendix D. Segwit is an
architectural
change to the structure of a transaction, which moves the unlocking script
(witness)
from inside the transaction to an external data structure (segregating
it). Segwit was initially envisioned as a hard fork upgrade, as it
modified a fundamental structure
(transaction). In November 2015, a developer working on Bitcoin Core
proposed a
mechanism by which segwit could be introduced as a soft fork. The
mechanism used
for this is a modification of the locking script of UTXO created under
segwit rules,
such that unmodified clients see the locking script as redeemable with any
unlocking
script whatsoever. As a result, segwit can be introduced without requiring
every node
to upgrade or split from the chain: a soft fork.
It is likely that there are other, yet to be discovered, mechanisms by
which upgrades
can be made in a forward-compatible way as a soft fork.
Criticisms of Soft Forks
Soft forks based on the NOP opcodes are relatively uncontroversial. The
NOP
opcodes were placed in Bitcoin Script with the explicit goal of allowing
non-
disruptive upgrades.
However, many developers are concerned that other methods of soft fork
upgrades
make unacceptable tradeoffs. Common criticisms of soft fork changes
include:
Technical debt
Because soft forks are more technically complex than a hard fork upgrade,
they
introduce technical debt, a term that refers to increasing the future cost
of code
maintenance because of design tradeoffs made in the past. Code complexity
in
turn increases the likelihood of bugs and security vulnerabilities.
Unmodified clients see transactions as valid, without evaluating the
modified
consensus rules. In effect, the unmodified clients are not validating
using the full
range of consensus rules, as they are blind to the new rules. This applies
to NOP-
based upgrades, as well as other soft fork upgrades.
Irreversible upgrades
Because soft forks create transactions with additional consensus
constraints, they
become irreversible upgrades in practice. If a soft fork upgrade were to
be
reversed after being activated, any transactions created under the new
rules could
result in a loss of funds under the old rules. For example, if a CLTV
transaction is
evaluated under the old rules, there is no timelock constraint and it can
be spent
whenever. Therefore, critics contend that a failed soft fork that had to
be reversed
because of a bug would almost certainly lead to loss of funds.
Soft Fork Signaling with Block Version
Since soft forks allow unmodified clients to continue to operate within
consensus, the
mechanism for “activating” a soft fork is through miners signaling
readiness: a majority of miners must agree that they are ready and willing
to enforce the new consensus
rules. To coordinate their actions, there is a signaling mechanism that
allows them to
show their support for a consensus rule change. This mechanism was
introduced
with the activation of BIP-34 in March 2013 and replaced by the activation
of BIP-9
in July 2016.
The first implementation, in BIP-34, used the block version field to
allow miners to
signal readiness for a specific consensus rule change. Prior to BIP-34,
the block ver‐
sion was set to “1” by convention not enforced by consensus.
BIP-34 defined a consensus rule change that required the coinbase field
(input) of the
coinbase transaction to contain the block height. Prior to BIP-34, the
coinbase could
contain any arbitrary data the miners chose to include. After activation
of BIP-34,
valid blocks had to contain a specific block-height at the beginning of
the coinbase
and be identified with a version number greater than or equal to “2.”
To signal the change and activation of BIP-34, miners set the block
version to “2,”
instead of “1.” This did not immediately make version “1” blocks invalid.
Once activa‐
ted, version “1” blocks would become invalid and all version “2” blocks
would be
required to contain the block height in the coinbase to be valid.
BIP-34 defined a two-step activation mechanism, based on a rolling window
of 1000
blocks. A miner would signal his or her individual readiness for BIP-34 by
construct‐
ing blocks with “2” as the version number. Strictly speaking, these blocks
did not yet
have to comply with the new consensus rule of including the block-height
in the
coinbase transaction because the consensus rule had not yet been
activated. The con‐
sensus rules activated in two steps:
• If 75% (750 of the most recent 1000 blocks) are marked with version “2,”
then
version “2” blocks must contain block height in the coinbase transaction
or they
are rejected as invalid. Version “1” blocks are still accepted by the
network and
do not need to contain block-height. The old and new consensus rules
coexist
during this period.
• When 95% (950 of the most recent 1000 blocks) are version “2,” version
“1”
blocks are no longer considered valid. Version “2” blocks are valid only
if they
contain the block-height in the coinbase (as per the previous threshold).
There‐
after, all blocks must comply with the new consensus rules, and all valid
blocks
must contain block-height in the coinbase transaction.
After successful signaling and activation under the BIP-34 rules, this
mechanism was
used twice more to activate soft forks:
• BIP-66 Strict DER Encoding of Signatures was activated by BIP-34 style
signaling
with a block version “3” and invalidating version “2” blocks.
• BIP-65 CHECKLOCKTIMEVERIFY was activated by BIP-34 style signaling with
a
block version “4” and invalidating version “3” blocks.
After the activation of BIP-65, the signaling and activation mechanism of
BIP-34 was
retired and replaced with the BIP-9 signaling mechanism described next.
The standard is defined in BIP-34 (Block v2, Height in Coinbase).
BIP-9 Signaling and Activation
The mechanism used by BIP-34, BIP-66, and BIP-65 was successful in
activating three
soft forks. However, it was replaced because it had several limitations:
• By using the integer value of the block version, only one soft fork
could be activa‐
ted at a time, so it required coordination between soft fork proposals and
agree‐
ment on their prioritization and sequencing.
• Furthermore, because the block version was incremented, the mechanism
didn’t
offer a straightforward way to reject a change and then propose a
different one. If
old clients were still running, they could mistake signaling for a new
change as
signaling for the previously rejected change.
• Each new change irrevocably reduced the available block versions for
future
changes.
BIP-9 was proposed to overcome these challenges and improve the rate and
ease of
implementing future changes.
BIP-9 interprets the block version as a bit field instead of an integer.
Because the
block version was originally used as an integer, versions 1 through 4,
only 29 bits
remain available to be used as a bit field. This leaves 29 bits that can
be used to inde‐
pendently and simultaneously signal readiness on 29 different proposals.
BIP-9 also sets a maximum time for signaling and activation. This way
miners don’t
need to signal forever. If a proposal is not activated within the TIMEOUT
period
(defined in the proposal), the proposal is considered rejected. The
proposal may be
resubmitted for signaling with a different bit, renewing the activation
period.
Furthermore, after the TIMEOUT has passed and a feature has been activated
or rejec‐
ted, the signaling bit can be reused for another feature without
confusion. Therefore,
up to 29 changes can be signaled in parallel and after TIMEOUT the bits
can be “recy‐
cled” to propose new changes.
stable state of this system with only a few changes possible if there is
strong consen‐
sus by a very large majority. The 95% threshold for soft forks is
reflective of this real‐
ity.
It is important to recognize that there is no perfect solution for
consensus develop‐
ment. Both hard forks and soft forks involve tradeoffs. For some types of
changes,
soft forks may be a better choice; for others, hard forks may be a better
choice. There
is no perfect choice; both carry risks. The one constant characteristic of
consensus
software development is that change is difficult and consensus forces
compromise.
Some see this as a weakness of consensus systems. In time, you may come to
see it as
I do, as the system’s greatest strength.
without vulnerabilities should be vulnerable only to a compromise of the
bitcoin con‐
sensus mechanism, meaning that its root of trust is based on the strongest
part of the
bitcoin security architecture.
The numerous examples of hacked bitcoin exchanges serve to underscore this
point
because their security architecture and design fails even under the most
casual scru‐
tiny. These centralized implementations had invested trust explicitly in
numerous
components outside the bitcoin blockchain, such as hot wallets,
centralized ledger
databases, vulnerable encryption keys, and similar schemes.
User Security Best Practices
Humans have used physical security controls for thousands of years. By
comparison,
our experience with digital security is less than 50 years old. Modern
general-purpose
operating systems are not very secure and not particularly suited to
storing digital
money. Our computers are constantly exposed to external threats via
always-on inter‐
net connections. They run thousands of software components from hundreds
of
authors, often with unconstrained access to the user’s files. A single
piece of rogue
software, among the many thousands installed on your computer, can
compromise
your keyboard and files, stealing any bitcoin stored in wallet
applications. The level of
computer maintenance required to keep a computer virus-free and
trojan-free is
beyond the skill level of all but a tiny minority of computer users.
Despite decades of research and advancements in information security,
digital assets
are still woefully vulnerable to a determined adversary. Even the most
highly pro‐
tected and restricted systems, in financial services companies,
intelligence agencies,
and defense contractors, are frequently breached. Bitcoin creates digital
assets that
have intrinsic value and can be stolen and diverted to new owners
instantly and irrev‐
ocably. This creates a massive incentive for hackers. Until now, hackers
had to convert
identity information or account tokens—such as credit cards and bank
accounts—
into value after compromising them. Despite the difficulty of fencing and
laundering
financial information, we have seen ever-escalating thefts. Bitcoin
escalates this prob‐
lem because it doesn’t need to be fenced or laundered; it is intrinsic
value within a
digital asset.
Fortunately, bitcoin also creates the incentives to improve computer
security.
Whereas previously the risk of computer compromise was vague and indirect,
bitcoin
makes these risks clear and obvious. Holding bitcoin on a computer serves
to focus
the user’s mind on the need for improved computer security. As a direct
result of the
proliferation and increased adoption of bitcoin and other digital
currencies, we have
seen an escalation in both hacking techniques and security solutions. In
simple terms,
hackers now have a very juicy target and users have a clear incentive to
defend them‐
selves.
CHAPTER 12
Applications
Let’s now build on our understanding of bitcoin by looking at it as an
application plat‐
form. Nowadays, many people use the term “blockchain” to refer to any
application
platform that shares the design principles of bitcoin. The term is often
misused and
applied to many things that fail to deliver the primary features that
bitcoin’s block‐
chain delivers.
In this chapter we will look at the features offered by the bitcoin
blockchain, as an
application platform. We will consider the application building
primitives, which
form the building blocks of any blockchain application. We will look at
several impor‐
tant applications that use these primitives, such as colored coins,
payment (state)
channels, and routed payment channels (Lightning Network).
Introduction
The bitcoin system was designed as a decentralized currency and payment
system.
However, most of its functionality is derived from much lower-level
constructs that
can be used for much broader applications. Bitcoin wasn’t built with
components
such as accounts, users, balances, and payments. Instead, it uses a
transactional
scripting language with low-level cryptographic functions, as we saw in
Chapter 6.
Just like the higher-level concepts of accounts, balances, and payments
can be derived
from these basic primitives, so can many other complex applications. Thus,
the bit‐
coin blockchain can become an application platform offering trust services
to appli‐
cations, such as smart contracts, far surpassing the original purpose of
digital
currency and payments.
275
Predictable Issuance
Less than 21 million bitcoin will be issued, at a predictable rate.
The list of building blocks is not complete and more are added with each
new feature
introduced into bitcoin.
Applications from Building Blocks
The building blocks offered by bitcoin are elements of a trust platform
that can be
used to compose applications. Here are some examples of applications that
exist
today and the building blocks they use:
Proof-of-Existence (Digital Notary)
Immutability + Timestamp + Durability. A digital fingerprint can be
committed
with a transaction to the blockchain, proving that a document existed
(Time‐
stamp) at the time it was recorded. The fingerprint cannot be modified
ex-post-
facto (Immutability) and the proof will be stored permanently
(Durability).
Kickstarter (Lighthouse)
Consistency + Atomicity + Integrity. If you sign one input and the output
(Integ‐
rity) of a fundraiser transaction, others can contribute to the fundraiser
but it
cannot be spent (Atomicity) until the goal (output value) is funded
(Consis‐
tency).
Payment Channels
Quorum of Control + Timelock + No Double Spend + Nonexpiration + Censor‐
ship Resistance + Authorization. A multisig 2-of-2 (Quorum) with a
timelock
(Timelock) used as the “settlement” transaction of a payment channel can
be held
(Nonexpiration) and spent whenever (Censorship Resistance) by either party
(Authorization). The two parties can then create commitment transactions
that
double-spend (No Double-Spend) the settlement on a shorter timelock (Time‐
lock).
Colored Coins
The first blockchain application we will discuss is colored coins.
Colored coins refers to a set of similar technologies that use bitcoin
transactions to
record the creation, ownership, and transfer of extrinsic assets other
than bitcoin. By
“extrinsic” we mean assets that are not stored directly on the bitcoin
blockchain, as
opposed to bitcoin itself, which is an asset intrinsic to the blockchain.
Colored coins are used to track digital assets as well as physical assets
held by third
parties and traded through colored coins certificates of ownership.
Digital asset col‐
ored coins can represent intangible assets such as a stock certificate,
license, virtual
278
|
Chapter 12: Blockchain Applications
property (game items), or most any form of licensed intellectual property
(trade‐
marks, copyrights, etc.). Tangible asset colored coins can represent
certificates of
ownership of commodities (gold, silver, oil), land title, automobiles,
boats, aircraft,
etc.
The term derives from the idea of “coloring” or marking a nominal amount
of bit‐
coin, for example, a single satoshi, to represent something other than the
bitcoin
value itself. As an analogy, consider stamping a $1 note with a message
saying, “this is
a stock certificate of ACME” or “this note can be redeemed for 1 oz of
silver” and
then trading the $1 note as a certificate of ownership of this other
asset. The first
implementation of colored coins, named Enhanced Padded-Order-Based
Coloring or
EPOBC, assigned extrinsic assets to a 1-satoshi output. In this way, it
was a true “col‐
ored coin,” as each asset was added as an attribute (color) of a single
satoshi.
More recent implementations of colored coins use the OP_RETURN script
opcode to
store metadata in a transaction, in conjunction with external data stores
that associate
the metadata to specific assets.
The two most prominent implementations of colored coins today are Open
Assets and
Colored Coins by Colu. These two systems use different approaches to
colored coins
and are not compatible. Colored coins created in one system cannot be seen
or used
in the other system.
Using Colored Coins
Colored coins are created, transferred, and generally viewed in special
wallets that
can interpret the colored coins protocol metadata attached to bitcoin
transactions.
Special care must be taken to avoid using a colored-coin–related key in a
regular bit‐
coin wallet, as the regular wallet may destroy the metadata. Similarly,
colored coins
should not be sent to addresses managed by regular wallets, but only to
addresses that
are managed by wallets that are colored-coin-aware. Both Colu and Open
Assets sys‐
tems use special colored-coin addresses to mitigate this risk and to
ensure that col‐
ored coins are not sent to unaware wallets.
Colored coins are also not visible to most general-purpose blockchain
explorers.
Instead, you must use a colored-coins explorer to interpret the metadata
of a colored
coins transaction.
An Open Assets-compatible wallet application and blockchain explorer can
be found
at coinprism.
A Colu Colored Coins-compatible wallet application and blockchain explorer
can be
found at Blockchain Explorer.
A Copay wallet plug-in can be found at Colored Coins Copay Addon.
Colored Coins
|
279
Issuing Colored Coins
Each of the colored coins implementations has a different way of creating
colored
coins, but they all provide similar functionality. The process of creating
a colored
coin asset is called issuance. An initial transaction, the issuance
transaction registers
the asset on the bitcoin blockchain and creates an asset ID that is used
to reference
the asset. Once issued, assets can be transferred between addresses using
transfer
transactions.
Assets issued as colored coins can have multiple properties. They can be
divisible or
indivisible, meaning that the amount of asset in a transfer can be an
integer (e.g., 5) or
have decimal subdivision (e.g., 4.321). Assets can also have fixed
issuance, meaning a
certain amount are issued only once, or can be reissued, meaning that new
units of
the asset can be issued by the original issuer after the initial issuance.
Finally, some colored coins enable dividends, allowing the distribution of
bitcoin pay‐
ments to the owners of a colored coin asset in proportion to their
ownership.
Colored Coins Transactions
The metadata that gives meaning to a colored coin transaction is usually
stored in
one of the outputs using the OP_RETURN opcode. Different colored coins
protocols use
different encodings for the content of the OP_RETURN data. The output
containing the
OP_RETURN is called the marker output.
The order of the outputs and position of the marker output may have
special mean‐
ing in the colored coins protocol. In Open Assets, for example, any
outputs before the
marker output represent asset issuance. Any outputs after the marker
represent asset
transfer. The marker output assigns specific values and colors to the
other outputs by
referencing their order in the transaction.
In Colored Coins (Colu), by comparison, the marker output encodes an
opcode that
determines how the metadata is interpreted. Opcodes 0x01 through 0x0F
indicate an
issuance transaction. An issuance opcode is usually followed by an asset
ID or other
identifier that can be used to retrieve the asset information from an
external source
(e.g., bittorrent). Opcodes 0x10 through 0x1F represent a transfer
transaction. Trans‐
fer transaction metadata contain simple scripts that transfer specific
amounts of
assets from inputs to outputs, by reference to their index. Ordering of
inputs and out‐
puts is therefore important in the interpretation of the script.
If the metadata is too long to fit in OP_RETURN, the colored coins
protocol may use
other “tricks” to store metadata in a transaction. Examples include
putting metadata
in a redeem script, followed by OP_DROP opcodes to ensure the script
ignores the
metadata. Another mechanism used is a 1-of-N multisig script where only
the first
280
|
Chapter 12: Blockchain Applications
public key is a real public key that can spend the output and subsequent
“keys” are
replaced by encoded metadata.
In order to correctly interpret the metadata in a colored coins
transaction you must
use a compatible wallet or block explorer. Otherwise, the transaction
looks like a
“normal” bitcoin transaction with an OP_RETURN output.
As an example, I created and issued a MasterBTC asset using colored coins.
The Mas‐
terBTC asset represents a voucher for a free copy of this book. These
vouchers can be
transferred, traded, and redeemed using a colored coins-compatible wallet.
For this particular example, I used the wallet and explorer at
https://coinprism.info,
which uses the Open Assets colored coins protocol.
Малюнок 12-1 shows the issuance transaction using the Coinprism
block explorer:
https://www.coinprism.info/tx/
10d7c4e022f35288779be6713471151ede967caaa39eecd35296aa36d9c109ec)
Малюнок 12-1. The issuance transaction as viewed on coinprism.info
As you can see, coinprism shows the issuance of 20 units of “Free copy of
Mastering
Bitcoin,” the MasterBTC asset, to a special colored coin address:
akTnsDt5uzpioRST76VFRQM8q8sBFnQiwcx
Any funds or colored assets sent to this address will be lost forever.
Do not send value to this example address!
Colored Coins
|
281
The transaction ID of the issuance transaction is a “normal” bitcoin
transaction ID.
Малюнок 12-2 shows that same transaction in a block explorer that
doesn’t decode col‐
ored coins. We’ll use blockchain.info:
https://blockchain.info/tx/
10d7c4e022f35288779be6713471151ede967caaa39eecd35296aa36d9c109ec
Малюнок 12-2. The issuance transaction on a block explorer that
doesn’t decode colored
coins
As you can see, blockchain.info doesn’t recognize this as a colored coins
transaction.
In fact, it marks the second output with “Unable to decode output address”
in red let‐
ters.
If you select “Show scripts & coinbase” on that screen, you can see
more detail about
the transaction (Малюнок 12-3).
Малюнок 12-3. The scripts in the issuance transaction
Once again, blockchain.info doesn’t understand the second output. It marks
it with
“Strange” in red letters. However, we can see that some of the metadata in
the marker
output is human-readable:
OP_RETURN
4f41010001141b753d68747470733a2f2f6370722e736d2f466f796b777248365559
(decoded) "OA____u=https://cpr.sm/FoykwrH6UY
Let’s retrieve the transaction using bitcoin-cli:
$ bitcoin-cli decoderawtransaction `bitcoin-cli getrawtransaction
10d7c4e022f35288779be6713471151ede967caaa39eecd35296aa36d9c109ec`
Stripping out the rest of the transaction, the second output looks like
this:
282
|
Chapter 12: Blockchain Applications
{
"value": 0.00000000,
"n": 1,
"scriptPubKey": "OP_RETURN
4f41010001141b753d68747470733a2f2f6370722e736d2f466f796b777248365559"
}
The prefix 4F41 represents the letters “OA”, which stands for “Open
Assets” and helps
us identify that what follows is metadata defined by the Open Assets
protocol. The
ASCII-encoded string that follows is a link to an asset definition:
u=https://cpr.sm/FoykwrH6UY
If we retrieve this URL, we get a JSON-encoded asset definition, as shown
here:
{
"asset_ids": [
"AcuRVsoa81hoLHmVTNXrRD8KpTqUXeqwgH"
],
"contract_url": null,
"name_short": "MasterBTC",
"name": "Free copy of \"Mastering Bitcoin\"",
"issuer": "Andreas M. Antonopoulos",
"description": "This token is redeemable for a free copy of the book
\"Master
ing Bitcoin\"",
"description_mime": "text/x-markdown; charset=UTF-8",
"type": "Other",
"divisibility": 0,
"link_to_website": false,
"icon_url": null,
"image_url": null,
"version": "1.0"
}
Counterparty
Counterparty is a protocol layer built on top of bitcoin. The Counterparty
protocol,
similar to colored coins, offers the ability to create and trade virtual
assets and tokens.
In addition, Counterparty offers a decentralized exchange for assets.
Counterparty is
also implementing smart contracts, based on the Ethereum Virtual Machine
(EVM).
Like the colored coins protocols, Counterparty embeds metadata in bitcoin
transac‐
tions, using the OP_RETURN opcode or 1-of-N multisignature addresses that
encode
metadata in the place of public keys. Using these mechanisms, Counterparty
imple‐
ments a protocol layer encoded in bitcoin transactions. The additional
protocol layer
can be interpreted by applications that are Counterparty-aware, such as
wallets and
blockchain explorers, or any application built using the Counterparty
libraries.
Counterparty
|
283
Counterparty can be used as a platform for other applications and
services, in turn.
For example, Tokenly is a platform built on top of Counterparty that
allows content
creators, artists, and companies to issue tokens that express digital
ownership and can
be used to rent, access, trade, or shop for content, products, and
services. Other appli‐
cations leveraging Counterparty include games (Spells of Genesis) and grid
comput‐
ing projects (Folding Coin).
More details about Counterparty can be found at https://counterparty.io.
The open
source project can be found at https://github.com/CounterpartyXCP.
Payment Channels and State Channels
Payment channels are a trustless mechanism for exchanging bitcoin
transactions
between two parties, outside of the bitcoin blockchain. These
transactions, which
would be valid if settled on the bitcoin blockchain, are held off-chain
instead, acting
as promissory notes for eventual batch settlement. Because the
transactions are not
settled, they can be exchanged without the usual settlement latency,
allowing
extremely high transaction throughput, low (submillisecond) latency, and
fine
(satoshi-level) granularity.
Actually, the term channel is a metaphor. State channels are virtual
constructs repre‐
sented by the exchange of state between two parties, outside of the
blockchain. There
are no “channels” per se and the underlying data transport mechanism is
not the
channel. We use the term channel to represent the relationship and shared
state
between two parties, outside of the blockchain.
To further explain this concept, think of a TCP stream. From the
perspective of
higher-level protocols it is a “socket” connecting two applications across
the internet.
But if you look at the network traffic, a TCP stream is just a virtual
channel over IP
packets. Each endpoint of the TCP stream sequences and assembles IP
packets to cre‐
ate the illusion of a stream of bytes. Underneath, it’s all disconnected
packets. Simi‐
larly, a payment channel is just a series of transactions. If properly
sequenced and
connected, they create redeemable obligations that you can trust even
though you
don’t trust the other side of the channel.
In this section we will look at various forms of payment channels. First,
we will exam‐
ine the mechanisms used to construct a one-way (unidirectional) payment
channel
for a metered micropayment service, such as streaming video. Then, we will
expand
on this mechanism and introduce bidirectional payment channels. Finally,
we will
look at how bidirectional channels can be connected end-to-end to form
multihop
channels in a routed network, first proposed under the name Lightning
Network.
Payment channels are part of the broader concept of a state channel, which
represents
an off-chain alteration of state, secured by eventual settlement in a
blockchain. A pay‐
284
| Chapter 12: Blockchain Applications
ment channel is a state channel where the state being altered is the
balance of a virtual
currency.
State Channels—Basic Concepts and Terminology
A state channel is established between two parties, through a transaction
that locks a
shared state on the blockchain. This is called the funding transaction or
anchor trans‐
action. This single transaction must be transmitted to the network and
mined to
establish the channel. In the example of a payment channel, the locked
state is the
initial balance (in currency) of the channel.
The two parties then exchange signed transactions, called commitment
transactions,
that alter the initial state. These transactions are valid transactions in
that they could
be submitted for settlement by either party, but instead are held
off-chain by each
party pending the channel closure. State updates can be created as fast as
each party
can create, sign, and transmit a transaction to the other party. In
practice this means
that thousands of transactions per second can be exchanged.
When exchanging commitment transactions the two parties also invalidate
the previ‐
ous states, so that the most up-to-date commitment transaction is always
the only one
that can be redeemed. This prevents either party from cheating by
unilaterally closing
the channel with an expired prior state that is more favorable to them
than the cur‐
rent state. We will examine the various mechanisms that can be used to
invalidate
prior state in the rest of this chapter.
Finally, the channel can be closed either cooperatively, by submitting a
final settle‐
ment transaction to the blockchain, or unilaterally, by either party
submitting the last
commitment transaction to the blockchain. A unilateral close option is
needed in
case one of the parties unexpectedly disconnects. The settlement
transaction repre‐
sents the final state of the channel and is settled on the blockchain.
In the entire lifetime of the channel, only two transactions need to be
submitted for
mining on the blockchain: the funding and settlement transactions. In
between these
two states, the two parties can exchange any number of commitment
transactions
that are never seen by anyone else, nor submitted to the blockchain.
Малюнок 12-4 illustrates a payment channel between Bob and Alice,
showing the fund‐
ing, commitment, and settlement transactions.
Payment Channels and State Channels
|
285
Малюнок 12-4. A payment channel between Bob and Alice, showing the
funding, commit‐
ment, and settlement transactions
Simple Payment Channel Example
To explain state channels, we have to start with a very simple example. We
demon‐
strate a one-way channel, meaning that value is flowing in one direction
only. We will
also start with the naive assumption that no one is trying to cheat, to
keep things sim‐
ple. Once we have the basic channel idea explained, we will then look at
what it takes
to make it trustless so that neither party can cheat, even if they are
trying to.
286
|
Chapter 12: Blockchain Applications
For this example we will assume two participants: Emma and Fabian. Fabian
offers a
video streaming service that is billed by the second using a micropayment
channel.
Fabian charges 0.01 millibit (0.00001 BTC) per second of video, equivalent
to 36 mil‐
libits (0.036 BTC) per hour of video. Emma is a user who purchases this
streaming
video service from Fabian. Малюнок 12-5 shows Emma buying the video
streaming ser‐
vice from Fabian using a payment channel.
Малюнок 12-5. Emma purchases streaming video from Fabian with a
payment channel,
paying for each second of video
In this example, Fabian and Emma are using special software that handles
both the
payment channel and the video streaming. Emma is running the software in
her
browser, Fabian is running it on a server. The software includes basic
bitcoin wallet
functionality and can create and sign bitcoin transactions. Both the
concept and the
term “payment channel” are completely hidden from the users. What they see
is video
that is paid for by the second.
To set up the payment channel, Emma and Fabian establish a 2-of-2
multisignature
address, with each of them holding one of the keys. From Emma’s
perspective, the
software in her browser presents a QR code with a P2SH address (starting
with “3”),
and asks her to submit a “deposit” for up to 1 hour of video. The address
is then fun‐
ded by Emma. Emma’s transaction, paying to the multisignature address, is
the fund‐
ing or anchor transaction for the payment channel.
For this example, let’s say that Emma funds the channel with 36 millibits
(0.036 BTC).
This will allow Emma to consume up to 1 hour of streaming video. The
funding
transaction in this case sets the maximum amount that can be transmitted
in this
channel, setting the channel capacity.
The funding transaction consumes one or more inputs from Emma’s wallet,
sourcing
the funds. It creates one output with a value of 36 millibits paid to the
multisignature
Payment Channels and State Channels
|
287
2-of-2 address controlled jointly between Emma and Fabian. It may have
additional
outputs for change back to Emma’s wallet.
Once the funding transaction is confirmed, Emma can start streaming video.
Emma’s
software creates and signs a commitment transaction that changes the
channel bal‐
ance to credit 0.01 millibit to Fabian’s address and refund 35.99
millibits back to
Emma. The transaction signed by Emma consumes the 36 millibits output
created by
the funding transaction and creates two outputs: one for her refund, the
other for
Fabian’s payment. The transaction is only partially signed—it requires two
signatures
(2-of-2), but only has Emma’s signature. When Fabian’s server receives
this transac‐
tion, it adds the second signature (for the 2-of-2 input) and returns it
to Emma
together with 1 second worth of video. Now both parties have a fully
signed commit‐
ment transaction that either can redeem, representing the correct
up-to-date balance
of the channel. Neither party broadcasts this transaction to the network.
In the next round, Emma’s software creates and signs another commitment
transac‐
tion (commitment #2) that consumes the same 2-of-2 output from the funding
trans‐
action. The second commitment transaction allocates one output of 0.2
millibits to
Fabian’s address and one output of 35.98 millibits back to Emma’s address.
This new
transaction is payment for two cumulative seconds of video. Fabian’s
software signs
and returns the second commitment transaction, together with the another
second of
video.
In this way, Emma’s software continues to send commitment transactions to
Fabian’s
server in exchange for streaming video. The balance of the channel
gradually accu‐
mulates in favor of Fabian, as Emma consumes more seconds of video. Let’s
say
Emma watches 600 seconds (10 minutes) of video, creating and signing 600
commit‐
ment transactions. The last commitment transaction (#600) will have two
outputs,
splitting the balance of the channel, 6 millibits to Fabian and 30
millibits to Emma.
Finally, Emma clicks “Stop” to stop streaming video. Either Fabian or Emma
can now
transmit the final state transaction for settlement. This last transaction
is the settle‐
ment transaction and pays Fabian for all the video Emma consumed,
refunding the
remainder of the funding transaction to Emma.
Малюнок 12-6 shows the channel between Emma and Fabian and the
commitment
transactions that update the balance of the channel.
In the end, only two transactions are recorded on the blockchain: the
funding trans‐
action that established the channel and a settlement transaction that
allocated the
final balance correctly between the two participants.
288
| Chapter 12: Blockchain Applications
Малюнок 12-6. Emma’s payment channel with Fabian, showing the
commitment transac‐
tions that update the balance of the channel
Making Trustless Channels
The channel we just described works, but only if both parties cooperate,
without any
failures or attempts to cheat. Let’s look at some of the scenarios that
break this chan‐
nel and see what is needed to fix those:
• Once the funding transaction happens, Emma needs Fabian’s signature to
get any
money back. If Fabian disappears, Emma’s funds are locked in a 2-of-2 and
effec‐
tively lost. This channel, as constructed, leads to a loss of funds if one
of the par‐
ties disconnects before there is at least one commitment transaction
signed by
both parties.
• While the channel is running, Emma can take any of the commitment
transac‐
tions Fabian has countersigned and transmit one to the blockchain. Why pay
for
Payment Channels and State Channels
|
289
600 seconds of video, if she can transmit commitment transaction #1 and
only
pay for 1 second of video? The channel fails because Emma can cheat by
broad‐
casting a prior commitment that is in her favor.
Both of these problems can be solved with timelocks—let’s look at how we
could use
transaction-level timelocks (nLocktime).
Emma cannot risk funding a 2-of-2 multisig unless she has a guaranteed
refund. To
solve this problem, Emma constructs the funding and refund transaction at
the same
time. She signs the funding transaction but doesn’t transmit it to anyone.
Emma
transmits only the refund transaction to Fabian and obtains his signature.
The refund transaction acts as the first commitment transaction and its
timelock
establishes the upper bound for the channel’s life. In this case, Emma
could set the
nLocktime to 30 days or 4320 blocks into the future. All subsequent
commitment
transactions must have a shorter timelock, so that they can be redeemed
before the
refund transaction.
Now that Emma has a fully signed refund transaction, she can confidently
transmit
the signed funding transaction knowing that she can eventually, after the
timelock
expires, redeem the refund transaction even if Fabian disappears.
Every commitment transaction the parties exchange during the life of the
channel
will be timelocked into the future. But the delay will be slightly shorter
for each com‐
mitment so the most recent commitment can be redeemed before the prior
commit‐
ment it invalidates. Because of the nLockTime, neither party can
successfully
propagate any of the commitment transactions until their timelock expires.
If all goes
well, they will cooperate and close the channel gracefully with a
settlement transac‐
tion, making it unnecessary to transmit an intermediate commitment
transaction. If
not, the most recent commitment transaction can be propagated to settle
the account
and invalidate all prior commitment transactions.
For example, if commitment transaction #1 is timelocked to 4320 blocks in
the
future, then commitment transaction #2 is timelocked to 4319 blocks in the
future.
Commitment transaction #600 can be spent 600 blocks before commitment
transac‐
tion #1 becomes valid.
Малюнок 12-7 shows each commitment transaction setting a shorter
timelock, allowing
it to be spent before the previous commitments become valid.
290
|
Chapter 12: Blockchain Applications
Малюнок 12-7. Each commitment sets a shorter timelock, allowing it
to be spent before the
previous commitments become valid
Each subsequent commitment transaction must have a shorter timelock so
that it
may be broadcast before its predecessors and before the refund
transaction. The abil‐
ity to broadcast a commitment earlier ensures it will be able to spend the
funding
output and preclude any other commitment transaction from being redeemed
by
spending the output. The guarantees offered by the bitcoin blockchain,
preventing
double-spends and enforcing timelocks, effectively allow each commitment
transac‐
tion to invalidate its predecessors.
State channels use timelocks to enforce smart contracts across a time
dimension. In
this example we saw how the time dimension guarantees that the most recent
com‐
mitment transaction becomes valid before any earlier commitments. Thus,
the most
recent commitment transaction can be transmitted, spending the inputs and
invalid‐
ating prior commitment transactions. The enforcement of smart contracts
with abso‐
lute timelocks protects against cheating by one of the parties. This
implementation
needs nothing more than absolute transaction-level timelocks (nLocktime).
Next, we
will see how script-level timelocks, CHECKLOCKTIMEVERIFY and
CHECKSEQUENCEVER
IFY, can be used to construct more flexible, useful, and sophisticated
state channels.
The first form of unidirectional payment channel was demonstrated as a
prototype
video streaming application in 2015 by an Argentinian team of developers.
You can
still see it at streamium.io.
Timelocks are not the only way to invalidate prior commitment
transactions. In the
next sections we will see how a revocation key can be used to achieve the
same result.
Timelocks are effective but they have two distinct disadvantages. By
establishing a
maximum timelock when the channel is first opened, they limit the lifetime
of the
channel. Worse, they force channel implementations to strike a balance
between
allowing long-lived channels and forcing one of the participants to wait a
very long
time for a refund in case of premature closure. For example, if you allow
the channel
to remain open for 30 days, by setting the refund timelock to 30 days, if
one of the
Payment Channels and State Channels
|
291
parties disappears immediately the other party must wait 30 days for a
refund. The
more distant the endpoint, the more distant the refund.
The second problem is that since each subsequent commitment transaction
must
decrement the timelock, there is an explicit limit on the number of
commitment
transactions that can be exchanged between the parties. For example, a
30-day chan‐
nel, setting a timelock of 4320 blocks into the future, can only
accommodate 4320
intermediate commitment transactions before it must be closed. There is a
danger in
setting the timelock commitment transaction interval at 1 block. By
setting the time‐
lock interval between commitment transactions to 1 block, a developer is
creating a
very high burden for the channel participants who have to be vigilant,
remain online
and watching, and be ready to transmit the right commitment transaction at
anytime.
Now that we understand how timelocks can be used to invalidate prior
commitments,
we can see the difference between closing the channel cooperatively and
closing it
unilaterally by broadcasting a commitment transaction. All commitment
transactions
are timelocked, therefore broadcasting a commitment transaction will
always involve
waiting until the timelock has expired. But if the two parties agree on
what the final
balance is and know they both hold commitment transactions that will
eventually
make that balance a reality, they can construct a settlement transaction
without a
timelock representing that same balance. In a cooperative close, either
party takes the
most recent commitment transaction and builds a settlement transaction
that is iden‐
tical in every way except that it omits the timelock. Both parties can
sign this settle‐
ment transaction knowing there is no way to cheat and get a more favorable
balance.
By cooperatively signing and transmitting the settlement transaction they
can close
the channel and redeem their balance immediately. Worst case, one of the
parties can
be petty, refuse to cooperate, and force the other party to do a
unilateral close with
the most recent commitment transaction. But if they do that, they have to
wait for
their funds too.
Asymmetric Revocable Commitments
A better way to handle the prior commitment states is to explicitly revoke
them.
However, this is not easy to achieve. A key characteristic of bitcoin is
that once a
transaction is valid, it remains valid and does not expire. The only way
to cancel a
transaction is by double-spending its inputs with another transaction
before it is
mined. That’s why we used timelocks in the simple payment channel example
above
to ensure that more recent commitments could be spent before older
commitments
were valid. However, sequencing commitments in time creates a number of
con‐
straints that make payment channels difficult to use.
Even though a transaction cannot be canceled, it can be constructed in
such a way as
to make it undesirable to use. The way we do that is by giving each party
a revocation
key that can be used to punish the other party if they try to cheat. This
mechanism for
292
| Chapter 12: Blockchain Applications
revoking prior commitment transactions was first proposed as part of the
Lightning
Network.
To explain revocation keys, we will construct a more complex payment
channel
between two exchanges run by Hitesh and Irene. Hitesh and Irene run
bitcoin
exchanges in India and the USA, respectively. Customers of Hitesh’s Indian
exchange
often send payments to customers of Irene’s USA exchange and vice versa.
Currently,
these transactions occur on the bitcoin blockchain, but this means paying
fees and
waiting several blocks for confirmations. Setting up a payment channel
between the
exchanges will significantly reduce the cost and accelerate the
transaction flow.
Hitesh and Irene start the channel by collaboratively constructing a
funding transac‐
tion, each funding the channel with 5 bitcoin. The initial balance is 5
bitcoin for
Hitesh and 5 bitcoin for Irene. The funding transaction locks the channel
state in a 2-
of-2 multisig, just like in the example of a simple channel.
The funding transaction may have one or more inputs from Hitesh (adding up
to 5
bitcoin or more), and one or more inputs from Irene (adding up to 5
bitcoin or
more). The inputs have to slightly exceed the channel capacity in order to
cover the
transaction fees. The transaction has one output that locks the 10 total
bitcoin to a 2-
of-2 multisig address controlled by both Hitesh and Irene. The funding
transaction
may also have one or more outputs returning change to Hitesh and Irene if
their
inputs exceeded their intended channel contribution. This is a single
transaction with
inputs offered and signed by two parties. It has to be constructed in
collaboration and
signed by each party before it is transmitted.
Now, instead of creating a single commitment transaction that both parties
sign,
Hitesh and Irene create two different commitment transactions that are
asymmetric.
Hitesh has a commitment transaction with two outputs. The first output
pays Irene
the 5 bitcoin she is owed immediately. The second output pays Hitesh the 5
bitcoin he
is owed, but only after a timelock of 1000 blocks. The transaction outputs
look like
this:
Input: 2-of-2 funding output, signed by Irene
Output 0 <5 bitcoin>:
<Irene's Public Key> CHECKSIG
Output 1:
<1000 blocks>
CHECKSEQUENCEVERIFY
DROP
<Hitesh's Public Key> CHECKSIG
Irene has a different commitment transaction with two outputs. The first
output pays
Hitesh the 5 bitcoin he is owed immediately. The second output pays Irene
the 5 bit‐
Payment Channels and State Channels
|
293
coin she is owed but only after a timelock of 1000 blocks. The commitment
transac‐
tion Irene holds (signed by Hitesh) looks like this:
Input: 2-of-2 funding output, signed by Hitesh
Output 0 <5 bitcoin>:
<Hitesh's Public Key> CHECKSIG
Output 1:
<1000 blocks>
CHECKSEQUENCEVERIFY
DROP
<Irene's Public Key> CHECKSIG
This way, each party has a commitment transaction, spending the 2-of-2
funding out‐
put. This input is signed by the other party. At any time the party
holding the transac‐
tion can also sign (completing the 2-of-2) and broadcast. However, if they
broadcast
the commitment transaction, it pays the other party immediately whereas
they have
to wait for a short timelock to expire. By imposing a delay on the
redemption of one
of the outputs, we put each party at a slight disadvantage when they
choose to unilat‐
erally broadcast a commitment transaction. But a time delay alone isn’t
enough to
encourage fair conduct.
Малюнок 12-8 shows two asymmetric commitment transactions, where the
output pay‐
ing the holder of the commitment is delayed.
Малюнок 12-8. Two asymmetric commitment transactions with delayed
payment for the
party holding the transaction
Now we introduce the final element of this scheme: a revocation key that
allows a
wronged party to punish a cheater by taking the entire balance of the
channel.
294
|
Chapter 12: Blockchain Applications
Each of the commitment transactions has a “delayed” output. The redemption
script
for that output allows one party to redeem it after 1000 blocks or the
other party to
redeem it if they have a revocation key. So when Hitesh creates a
commitment trans‐
action for Irene to sign, he makes the second output payable to himself
after 1000
blocks, or to whoever can present a revocation key. Hitesh constructs this
transaction
and creates a revocation key that he keeps secret. He will only reveal it
to Irene when
he is ready to move to a new channel state and wants to revoke this
commitment. The
second output’s script looks like this:
Output 0 <5 bitcoin>:
<Irene's Public Key> CHECKSIG
Output 1 <5 bitcoin>:
IF
# Revocation penalty output
<Revocation Public Key>
ELSE
<1000 blocks>
CHECKSEQUENCEVERIFY
DROP
<Hitesh's Public Key>
ENDIF
CHECKSIG
Irene can confidently sign this transaction, since if transmitted it will
immediately
pay her what she is owed. Hitesh holds the transaction, but knows that if
he transmits
it in a unilateral channel closing, he will have to wait 1000 blocks to
get paid.
When the channel is advanced to the next state, Hitesh has to revoke this
commit‐
ment transaction before Irene agrees to sign the next commitment
transaction. To do
that, all he has to do is send the revocation key to Irene. Once Irene has
the revocation
key for this commitment, she can sign the next commitment with confidence.
She
knows that if Hitesh tries to cheat by publishing the prior commitment,
she can use
the revocation key to redeem Hitesh’s delayed output. If Hitesh cheats,
Irene gets
BOTH outputs.
The revocation protocol is bilateral, meaning that in each round, as the
channel state
is advanced, the two parties exchange new commitments, exchange revocation
keys
for the previous commitment, and sign each other’s commitment
transactions. As
they accept a new state, they make the prior state impossible to use, by
giving each
other the necessary revocation keys to punish any cheating.
Let’s look at an example of how it works. One of Irene’s customers wants
to send 2
bitcoin to one of Hitesh’s customers. To transmit 2 bitcoin across the
channel, Hitesh
and Irene must advance the channel state to reflect the new balance. They
will com‐
mit to a new state (state number 2) where the channel’s 10 bitcoin are
split, 7 bitcoin
to Hitesh and 3 bitcoin to Irene. To advance the state of the channel,
they will each
create new commitment transactions reflecting the new channel balance.
Payment Channels and State Channels
|
295
As before, these commitment transactions are asymmetric so that the
commitment
transaction each party holds forces them to wait if they redeem it.
Crucially, before
signing new commitment transactions, they must first exchange revocation
keys to
invalidate the prior commitment. In this particular case, Hitesh’s
interests are aligned
with the real state of the channel and therefore he has no reason to
broadcast a prior
state. However, for Irene, state number 1 leaves her with a higher balance
than state 2.
When Irene gives Hitesh the revocation key for her prior commitment
transaction
(state number 1) she is effectively revoking her ability to profit from
regressing the
channel to a prior state because with the revocation key, Hitesh can
redeem both out‐
puts of the prior commitment transaction without delay. Meaning if Irene
broadcasts
the prior state, Hitesh can exercise his right to take all of the outputs.
Importantly, the revocation doesn’t happen automatically. While Hitesh has
the abil‐
ity to punish Irene for cheating, he has to watch the blockchain
diligently for signs of
cheating. If he sees a prior commitment transaction broadcast, he has 1000
blocks to
take action and use the revocation key to thwart Irene’s cheating and
punish her by
taking the entire balance, all 10 bitcoin.
Asymmetric revocable commitments with relative time locks (CSV) are a much
better
way to implement payment channels and a very significant innovation in
this tech‐
nology. With this construct, the channel can remain open indefinitely and
can have
billions of intermediate commitment transactions. In prototype
implementations of
Lightning Network, the commitment state is identified by a 48-bit index,
allowing
more than 281 trillion (2.8 x 1014) state transitions in any single
channel!
Hash Time Lock Contracts (HTLC)
Payment channels can be further extended with a special type of smart
contract that
allows the participants to commit funds to a redeemable secret, with an
expiration
time. This feature is called a Hash Time Lock Contract, or HTLC, and is
used in both
bidirectional and routed payment channels.
Let’s first explain the “hash” part of the HTLC. To create an HTLC, the
intended
recipient of the payment will first create a secret R. They then calculate
the hash of
this secret H:
H = Hash(R)
This produces a hash H that can be included in an output’s locking script.
Whoever
knows the secret can use it to redeem the output. The secret R is also
referred to as a
preimage to the hash function. The preimage is just the data that is used
as input to a
hash function.
The second part of an HTLC is the “time lock” component. If the secret is
not
revealed, the payer of the HTLC can get a “refund” after some time. This
is achieved
with an absolute time lock using CHECKLOCKTIMEVERIFY.
296
|
Chapter 12: Blockchain Applications
The script implementing an HTLC might look like this:
IF
# Payment if you have the secret R
HASH160 <H> EQUALVERIFY
ELSE
# Refund after timeout.
<locktime> CHECKLOCKTIMEVERIFY DROP
<Payee Pubic Key> CHECKSIG
ENDIF
Anyone who knows the secret R, which when hashed equals to H, can redeem
this out‐
put by exercising the first clause of the IF flow.
If the secret is not revealed and the HTLC claimed, after a certain number
of blocks
the payee can claim a refund using the second clause in the IF flow.
This is a basic implementation of an HTLC. This type of HTLC can be
redeemed by
anyone who has the secret R. An HTLC can take many different forms with
slight var‐
iations to the script. For example, adding a CHECKSIG operator and a
public key in the
first clause restricts redemption of the hash to a named recipient, who
must also
know the secret R.
Routed Payment Channels (Lightning Network)
The Lightning Network is a proposed routed network of bidirectional
payment chan‐
nels connected end-to-end. A network like this can allow any participant
to route a
payment from channel to channel without trusting any of the
intermediaries. The
Lightning Network was first described by Joseph Poon and Thadeus Dryja in
Febru‐
ary 2015, building on the concept of payment channels as proposed and
elaborated
upon by many others.
“Lightning Network” refers to a specific design for a routed payment
channel net‐
work, which has now been implemented by at least five different open
source teams.
The independent implementations are coordinated by a set of
interoperability stand‐
ards described in the Basics of Lightning Technology (BOLT) paper.
Prototype implementations of the Lightning Network have been released by
several
teams. For now, these implementations can only be run on testnet because
they use
segwit, which is not activated on the main bitcoin blockchain (mainnet).
The Lightning Network is one possible way of implementing routed payment
chan‐
nels. There are several other designs that aim to achieve similar goals,
such as Tee‐
chan and Tumblebit.
Routed Payment Channels (Lightning Network)
|
297
Basic Lightning Network Example
Let’s see how this works.
In this example, we have five participants: Alice, Bob, Carol, Diana, and
Eric. These
five participants have opened payment channels with each other, in pairs.
Alice has a
payment channel with Bob. Bob is connected to Carol, Carol to Diana, and
Diana to
Eric. For simplicity let’s assume each channel is funded with 2 bitcoin by
each partici‐
pant, for a total capacity of 4 bitcoin in each channel.
Малюнок 12-9 shows five participants in a Lightning Network,
connected by bidirec‐
tional payment channels that can be linked to make a payment from Alice to
Eric
(“Routed Payment Channels (Lightning Network)” on page 297).
Малюнок 12-9. A series of bidirectional payment channels linked to
form a Lightning Net‐
work that can route a payment from Alice to Eric
Alice wants to pay Eric 1 bitcoin. However, Alice is not connected to Eric
by a pay‐
ment channel. Creating a payment channel requires a funding transaction,
which
must be committed to the bitcoin blockchain. Alice does not want to open a
new pay‐
ment channel and commit more of her funds. Is there a way to pay Eric,
indirectly?
Малюнок 12-10 shows the step-by-step process of routing a payment
from Alice to Eric,
through a series of HTLC commitments on the payment channels connecting
the
participants.
298
|
Chapter 12: Blockchain Applications
Малюнок 12-10. Step-by-step payment routing through a Lightning
Network
Alice is running a Lightning Network (LN) node that is keeping track of
her payment
channel to Bob and has the ability to discover routes between payment
channels. Ali‐
ce’s LN node also has the ability to connect over the internet to Eric’s
LN node. Eric’s
LN node creates a secret R using a random number generator. Eric’s node
does not
reveal this secret to anyone. Instead, Eric’s node calculates a hash H of
the secret R and
transmits this hash to Alice’s node (see Малюнок 12-10 step 1).
Now Alice’s LN node constructs a route between Alice’s LN node and Eric’s
LN node.
The routing algorithm used will be examined in more detail later, but for
now let’s
assume that Alice’s node can find an efficient route.
Alice’s node then constructs an HTLC, payable to the hash H, with a
10-block refund
timeout (current block + 10), for an amount of 1.003 bitcoin (see
Малюнок 12-10 step
2). The extra 0.003 will be used to compensate the intermediate nodes for
their partic‐
ipation in this payment route. Alice offers this HTLC to Bob, deducting
1.003 bitcoin
from her channel balance with Bob and committing it to the HTLC. The HTLC
has
the following meaning: “Alice is committing 1.003 of her channel balance
to be paid to
Bob if Bob knows the secret, or refunded back to Alice’s balance if 10
blocks elapse.” The
channel balance between Alice and Bob is now expressed by commitment
transac‐
tions with three outputs: 2 bitcoin balance to Bob, 0.997 bitcoin balance
to Alice,
Routed Payment Channels (Lightning Network)
|
299
1.003 bitcoin committed in Alice’s HTLC. Alice’s balance is reduced by the
amount
committed to the HTLC.
Bob now has a commitment that if he is able to get the secret R within the
next 10
blocks, he can claim the 1.003 locked by Alice. With this commitment in
hand, Bob’s
node constructs an HTLC on his payment channel with Carol. Bob’s HTLC
commits
1.002 bitcoin to hash H for 9 blocks, which Carol can redeem if she has
secret R (see
Малюнок 12-10 step 3). Bob knows that if Carol can claim his HTLC,
she has to produce
R. If Bob has R in nine blocks, he can use it to claim Alice’s HTLC to
him. He also
makes 0.001 bitcoin for committing his channel balance for nine blocks. If
Carol is
unable to claim his HTLC and he is unable to claim Alice’s HTLC,
everything reverts
back to the prior channel balances and no one is at a loss. The channel
balance
between Bob and Carol is now: 2 to Carol, 0.998 to Bob, 1.002 committed by
Bob to
the HTLC.
Carol now has a commitment that if she gets R within the next nine blocks,
she can
claim 1.002 bitcoin locked by Bob. Now she can make an HTLC commitment on
her
channel with Diana. She commits an HTLC of 1.001 bitcoin to hash H, for
eight
blocks, which Diana can redeem if she has secret R (see Малюнок
12-10 step 4). From
Carol’s perspective, if this works she is 0.001 bitcoin better off and if
it doesn’t she
loses nothing. Her HTLC to Diana is only viable if R is revealed, at which
point she
can claim the HTLC from Bob. The channel balance between Carol and Diana
is
now: 2 to Diana, 0.999 to Carol, 1.001 committed by Carol to the HTLC.
Finally, Diana can offer an HTLC to Eric, committing 1 bitcoin for seven
blocks to
hash H (see Малюнок 12-10 step 5). The channel balance between Diana
and Eric is now:
2 to Eric, 1 to Diana, 1 committed by Diana to the HTLC.
However, at this hop in the route, Eric has secret R. He can therefore
claim the HTLC
offered by Diana. He sends R to Diana and claims the 1 bitcoin, adding it
to his chan‐
nel balance (see Малюнок 12-10 step 6). The channel balance is now:
1 to Diana, 3 to
Eric.
Now, Diana has secret R. Therefore, she can now claim the HTLC from Carol.
Diana
transmits R to Carol and adds the 1.001 bitcoin to her channel balance
(see
Малюнок 12-10 step 7). Now the channel balance between Carol and
Diana is: 0.999 to
Carol, 3.001 to Diana. Diana has “earned” 0.001 for participating in this
payment
route.
Flowing back through the route, the secret R allows each participant to
claim the out‐
standing HTLCs. Carol claims 1.002 from Bob, setting the balance on their
channel
to: 0.998 to Bob, 3.002 to Carol (see Малюнок 12-10 step 8).
Finally, Bob claims the
HTLC from Alice (see Малюнок 12-10 step 9). Their channel balance is
updated as:
0.997 to Alice, 3.003 to Bob.
300
|
Chapter 12: Blockchain Applications
Alice has paid Eric 1 bitcoin without opening a channel to Eric. None of
the inter‐
mediate parties in the payment route had to trust each other. For the
short-term com‐
mitment of their funds in the channel they are able to earn a small fee,
with the only
risk being a small delay in refund if the channel was closed or the routed
payment
failed.
Lightning Network Transport and Routing
All communications between LN nodes are encrypted point-to-point. In
addition,
nodes have a long-term public key that they use as an identifier and to
authenticate
each other.
Whenever a node wishes to send a payment to another node, it must first
construct a
path through the network by connecting payment channels with sufficient
capacity.
Nodes advertise routing information, including what channels they have
open, how
much capacity each channel has, and what fees they charge to route
payments. The
routing information can be shared in a variety of ways and different
routing protocols
are likely to emerge as Lightning Network technology advances. Some
Lightning Net‐
work implementations use the IRC protocol as a convenient mechanism for
nodes to
announce routing information. Another implementation of route discovery
uses a
P2P model where nodes propagate channel announcements to their peers, in a
“flooding” model, similar to how bitcoin propagates transactions. Future
plans
include a proposal called Flare, which is a hybrid routing model with
local node
“neighborhoods” and longer-range beacon nodes.
In our previous example, Alice’s node uses one of these route discovery
mechanisms
to find one or more paths connecting her node to Eric’s node. Once Alice’s
node has
constructed a path, she will initialize that path through the network, by
propagating a
series of encrypted and nested instructions to connect each of the
adjacent payment
channels.
Importantly, this path is only known to Alice’s node. All other
participants in the pay‐
ment route see only the adjacent nodes. From Carol’s perspective, this
looks like a
payment from Bob to Diana. Carol does not know that Bob is actually
relaying a pay‐
ment from Alice. She also doesn’t know that Diana will be relaying a
payment to Eric.
This is a critical feature of the Lightning Network, because it ensures
privacy of pay‐
ments and makes it very difficult to apply surveillance, censorship, or
blacklists. But
how does Alice establish this payment path, without revealing anything to
the inter‐
mediary nodes?
The Lightning Network implements an onion-routed protocol based on a
scheme
called Sphinx. This routing protocol ensures that a payment sender can
construct and
communicate a path through the Lightning Network such that:
Routed Payment Channels (Lightning Network)
|
301
• Intermediate nodes can verify and decrypt their portion of route
information
and find the next hop.
• Other than the previous and next hops, they cannot learn about any other
nodes
that are part of the path.
• They cannot identify the length of the payment path, or their own
position in
that path.
• Each part of the path is encrypted in such a way that a network-level
attacker
cannot associate the packets from different parts of the path to each
other.
• Unlike Tor (an onion-routed anonymization protocol on the internet),
there are
no “exit nodes” that can be placed under surveillance. The payments do not
need
to be transmitted to the bitcoin blockchain; the nodes just update channel
balan‐
ces.
Using this onion-routed protocol, Alice wraps each element of the path in
a layer of
encryption, starting with the end and working backward. She encrypts a
message to
Eric with Eric’s public key. This message is wrapped in a message
encrypted to Diana,
identifying Eric as the next recipient. The message to Diana is wrapped in
a message
encrypted to Carol’s public key and identifying Diana as the next
recipient. The mes‐
sage to Carol is encrypted to Bob’s key. Thus, Alice has constructed this
encrypted
multilayer “onion” of messages. She sends this to Bob, who can only
decrypt and
unwrap the outer layer. Inside, Bob finds a message addressed to Carol
that he can
forward to Carol but cannot decipher himself. Following the path, the
messages get
forwarded, decrypted, forwarded, etc., all the way to Eric. Each
participant knows
only the previous and next node in each hop.
Each element of the path contains information on the HTLC that must be
extended
to the next hop, the amount that is being sent, the fee to include, and
the CLTV lock‐
time (in blocks) expiration of the HTLC. As the route information
propagates, the
nodes make HTLC commitments forward to the next hop.
At this point, you might be wondering how it is possible that the nodes do
not know
the length of the path and their position in that path. After all, they
receive a message
and forward it to the next hop. Doesn’t it get shorter, allowing them to
deduce the
path size and their position? To prevent this, the path is always fixed at
20 hops and
padded with random data. Each node sees the next hop and a fixed-length
encrypted
message to forward. Only the final recipient sees that there is no next
hop. To every‐
one else it seems as if there are always 20 more hops to go.
302
|
Chapter 12: Blockchain Applications
Lightning Network Benefits
A Lightning Network is a second-layer routing technology. It can be
applied to any
blockchain that supports some basic capabilities, such as multisignature
transactions,
timelocks, and basic smart contracts.
If a Lightning Network is layered on top of the bitcoin network, the
bitcoin network
can gain a significant increase in capacity, privacy, granularity, and
speed, without
sacrificing the principles of trustless operation without intermediaries:
Privacy
Lightning Network payments are much more private than payments on the bit‐
coin blockchain, as they are not public. While participants in a route can
see pay‐
ments propagated across their channels, they do not know the sender or
recipient.
Fungibility
A Lightning Network makes it much more difficult to apply surveillance and
blacklists on bitcoin, increasing the fungibility of the currency.
Speed
Bitcoin transactions using Lightning Network are settled in milliseconds,
rather
than minutes, as HTLCs are cleared without committing transactions to a
block.
Granularity
A Lightning Network can enable payments at least as small as the bitcoin
“dust”
limit, perhaps even smaller. Some proposals allow for subsatoshi
increments.
Capacity
A Lightning Network increases the capacity of the bitcoin system by
several
orders of magnitude. There is no practical upper bound to the number of
pay‐
ments per second that can be routed over a Lightning Network, as it
depends
only on the capacity and speed of each node.
Trustless Operation
A Lightning Network uses bitcoin transactions between nodes that operate
as
peers without trusting each other. Thus, a Lightning Network preserves the
prin‐
ciples of the bitcoin system, while expanding its operating parameters
signifi‐
cantly.
Of course, as mentioned previously, the Lightning Network protocol is not
the only
way to implement routed payment channels. Other proposed systems include
Tum‐
blebit and Teechan. At this time, however, the Lightning Network has
already been
deployed on testnet. Several different teams have developed competing
implementa‐
tions of LN and are working toward a common interoperability standard
(called
Routed Payment Channels (Lightning Network)
|
303
BOLT). It is likely that Lightning Network will be the first routed
payment channel
network to be deployed in production.
Conclusion
We have examined just a few of the emerging applications that can be built
using the
bitcoin blockchain as a trust platform. These applications expand the
scope of bitcoin
beyond payments and beyond financial instruments, to encompass many other
appli‐
cations where trust is critical. By decentralizing the basis of trust, the
bitcoin block‐
chain is a platform that will spawn many revolutionary applications in a
wide variety
of industries.
304
| Chapter 12: Blockchain Applications
APPENDIX A
The Bitcoin Whitepaper by Satoshi
Nakamoto
This is the original whitepaper, reproduced in its entirety exactly as
it was published by Satoshi Nakamoto in October 2008.
Bitcoin - A Peer-to-Peer Electronic Cash System
Satoshi Nakamoto
satoshin@gmx.com
www.bitcoin.org
Abstract. A purely peer-to-peer version of electronic cash would allow
online pay‐
ments to be sent directly from one party to another without going through
a financial
institution. Digital signatures provide part of the solution, but the main
benefits are
lost if a trusted third party is still required to prevent
double-spending. We propose a
solution to the double-spending problem using a peer-to-peer network. The
network
timestamps transactions by hashing them into an ongoing chain of
hash-based proof-
of-work, forming a record that cannot be changed without redoing the
proof-of-
work. The longest chain not only serves as proof of the sequence of events
witnessed,
but proof that it came from the largest pool of CPU power. As long as a
majority of
CPU power is controlled by nodes that are not cooperating to attack the
network,
they’ll generate the longest chain and outpace attackers. The network
itself requires
minimal structure. Messages are broadcast on a best effort basis, and
nodes can leave
and rejoin the network at will, accepting the longest proof-of-work chain
as proof of
what happened while they were gone.
305
Introduction
Commerce on the Internet has come to rely almost exclusively on financial
institu‐
tions serving as trusted third parties to process electronic payments.
While the sys‐
tem works well enough for most transactions, it still suffers from the
inherent
weaknesses of the trust based model. Completely non-reversible
transactions are not
really possible, since financial institutions cannot avoid mediating
disputes. The cost
of mediation increases transaction costs, limiting the minimum practical
transaction
size and cutting off the possibility for small casual transactions, and
there is a broader
cost in the loss of ability to make non-reversible payments for
nonreversible services.
With the possibility of reversal, the need for trust spreads. Merchants
must be wary of
their customers, hassling them for more information than they would
otherwise
need. A certain percentage of fraud is accepted as unavoidable. These
costs and pay‐
ment uncertainties can be avoided in person by using physical currency,
but no
mechanism exists to make payments over a communications channel without a
trus‐
ted party.
What is needed is an electronic payment system based on cryptographic
proof
instead of trust, allowing any two willing parties to transact directly
with each other
without the need for a trusted third party. Transactions that are
computationally
impractical to reverse would protect sellers from fraud, and routine
escrow mecha‐
nisms could easily be implemented to protect buyers. In this paper, we
propose a sol‐
ution to the double-spending problem using a peer-to-peer distributed
timestamp
server to generate computational proof of the chronological order of
transactions.
The system is secure as long as honest nodes collectively control more CPU
power
than any cooperating group of attacker nodes.
Transactions
We define an electronic coin as a chain of digital signatures. Each owner
transfers the
coin to the next by digitally signing a hash of the previous transaction
and the public
key of the next owner and adding these to the end of the coin. A payee can
verify the
signatures to verify the chain of ownership.
306
|
Appendix A: The Bitcoin Whitepaper by Satoshi Nakamoto
The problem of course is the payee can’t verify that one of the owners did
not double-
spend the coin. A common solution is to introduce a trusted central
authority, or
mint, that checks every transaction for double spending. After each
transaction, the
coin must be returned to the mint to issue a new coin, and only coins
issued directly
from the mint are trusted not to be double-spent. The problem with this
solution is
that the fate of the entire money system depends on the company running
the mint,
with every transaction having to go through them, just like a bank.
We need a way for the payee to know that the previous owners did not sign
any ear‐
lier transactions. For our purposes, the earliest transaction is the one
that counts, so
we don’t care about later attempts to double-spend. The only way to
confirm the
absence of a transaction is to be aware of all transactions. In the mint
based model,
the mint was aware of all transactions and decided which arrived first. To
accomplish
this without a trusted party, transactions must be publicly announced [1],
and we
need a system for participants to agree on a single history of the order
in which they
were received. The payee needs proof that at the time of each transaction,
the major‐
ity of nodes agreed it was the first received.
Timestamp Server
The solution we propose begins with a timestamp server. A timestamp server
works
by taking a hash of a block of items to be timestamped and widely
publishing the
hash, such as in a newspaper or Usenet post [2-5]. The timestamp proves
that the
data must have existed at the time, obviously, in order to get into the
hash. Each time‐
stamp includes the previous timestamp in its hash, forming a chain, with
each addi‐
tional timestamp reinforcing the ones before it.
The Bitcoin Whitepaper by Satoshi Nakamoto
|
307
Proof-of-Work
To implement a distributed timestamp server on a peer-to-peer basis, we
will need to
use a proof-of-work system similar to Adam Back’s Hashcash [6], rather
than news‐
paper or Usenet posts. The proof-of-work involves scanning for a value
that when
hashed, such as with SHA-256, the hash begins with a number of zero bits.
The aver‐
age work required is exponential in the number of zero bits required and
can be veri‐
fied by executing a single hash. For our timestamp network, we implement
the proof-
of-work by incrementing a nonce in the block until a value is found that
gives the
block’s hash the required zero bits. Once the CPU effort has been expended
to make it
satisfy the proof-of-work, the block cannot be changed without redoing the
work. As
later blocks are chained after it, the work to change the block would
include redoing
all the blocks after it.
The proof-of-work also solves the problem of determining representation in
majority
decision making. If the majority were based on one-IP-address-one-vote, it
could be
subverted by anyone able to allocate many IPs. Proof-of-work is
essentially one-CPU-
one-vote. The majority decision is represented by the longest chain, which
has the
greatest proof-of-work effort invested in it. If a majority of CPU power
is controlled
by honest nodes, the honest chain will grow the fastest and outpace any
competing
chains. To modify a past block, an attacker would have to redo the
proof-of-work of
the block and all blocks after it and then catch up with and surpass the
work of the
honest nodes. We will show later that the probability of a slower attacker
catching up
diminishes exponentially as subsequent blocks are added.
To compensate for increasing hardware speed and varying interest in
running nodes
over time, the proof-of-work difficulty is determined by a moving average
targeting
an average number of blocks per hour. If they’re generated too fast, the
difficulty
increases.
308
|
Appendix A: The Bitcoin Whitepaper by Satoshi Nakamoto
Network
The steps to run the network are as follows:
1. New transactions are broadcast to all nodes.
2. Each node collects new transactions into a block.
3. Each node works on finding a difficult proof-of-work for its block.
4. When a node finds a proof-of-work, it broadcasts the block to all
nodes.
5. Nodes accept the block only if all transactions in it are valid and not
already
spent.
6. Nodes express their acceptance of the block by working on creating the
next
block in the chain, using the hash of the accepted block as the previous
hash.
Nodes always consider the longest chain to be the correct one and will
keep working
on extending it. If two nodes broadcast different versions of the next
block simultane‐
ously, some nodes may receive one or the other first. In that case, they
work on the
first one they received, but save the other branch in case it becomes
longer. The tie
will be broken when the next proof-of-work is found and one branch becomes
longer; the nodes that were working on the other branch will then switch
to the
longer one.
New transaction broadcasts do not necessarily need to reach all nodes. As
long as
they reach many nodes, they will get into a block before long. Block
broadcasts are
also tolerant of dropped messages. If a node does not receive a block, it
will request it
when it receives the next block and realizes it missed one.
Incentive
By convention, the first transaction in a block is a special transaction
that starts a new
coin owned by the creator of the block. This adds an incentive for nodes
to support
the network, and provides a way to initially distribute coins into
circulation, since
there is no central authority to issue them. The steady addition of a
constant of
amount of new coins is analogous to gold miners expending resources to add
gold to
circulation. In our case, it is CPU time and electricity that is expended.
The incentive can also be funded with transaction fees. If the output
value of a trans‐
action is less than its input value, the difference is a transaction fee
that is added to
the incentive value of the block containing the transaction. Once a
predetermined
number of coins have entered circulation, the incentive can transition
entirely to
transaction fees and be completely inflation free.
The incentive may help encourage nodes to stay honest. If a greedy
attacker is able to
assemble more CPU power than all the honest nodes, he would have to choose
The Bitcoin Whitepaper by Satoshi Nakamoto
|
309
between using it to defraud people by stealing back his payments, or using
it to gener‐
ate new coins. He ought to find it more profitable to play by the rules,
such rules that
favour him with more new coins than everyone else combined, than to
undermine
the system and the validity of his own wealth.
Reclaiming Disk Space
Once the latest transaction in a coin is buried under enough blocks, the
spent trans‐
actions before it can be discarded to save disk space. To facilitate this
without break‐
ing the block’s hash, transactions are hashed in a Merkle Tree [7] [2]
[5], with only the
root included in the block’s hash. Old blocks can then be compacted by
stubbing off
branches of the tree. The interior hashes do not need to be stored.
A block header with no transactions would be about 80 bytes. If we suppose
blocks
are generated every 10 minutes, 80 bytes * 6 * 24 * 365 == 4.2MB per year.
With
computer systems typically selling with 2GB of RAM as of 2008, and Moore’s
Law
predicting current growth of 1.2GB per year, storage should not be a
problem even if
the block headers must be kept in memory.
Simplified Payment Verification
It is possible to verify payments without running a full network node. A
user only
needs to keep a copy of the block headers of the longest proof-of-work
chain, which
he can get by querying network nodes until he’s convinced he has the
longest chain,
and obtain the Merkle branch linking the transaction to the block it’s
timestamped in.
He can’t check the transaction for himself, but by linking it to a place
in the chain, he
can see that a network node has accepted it, and blocks added after it
further confirm
the network has accepted it.
310
|
Appendix A: The Bitcoin Whitepaper by Satoshi Nakamoto
As such, the verification is reliable as long as honest nodes control the
network, but is
more vulnerable if the network is overpowered by an attacker. While
network nodes
can verify transactions for themselves, the simplified method can be
fooled by an
attacker’s fabricated transactions for as long as the attacker can
continue to over‐
power the network. One strategy to protect against this would be to accept
alerts
from network nodes when they detect an invalid block, prompting the user’s
software
to download the full block and alerted transactions to confirm the
inconsistency.
Businesses that receive frequent payments will probably still want to run
their own
nodes for more independent security and quicker verification.
Combining and Splitting Value
Although it would be possible to handle coins individually, it would be
unwieldy to
make a separate transaction for every cent in a transfer. To allow value
to be split and
combined, transactions contain multiple inputs and outputs. Normally there
will be
either a single input from a larger previous transaction or multiple
inputs combining
smaller amounts, and at most two outputs: one for the payment, and one
returning
the change, if any, back to the sender.
It should be noted that fan-out, where a transaction depends on several
transactions,
and those transactions depend on many more, is not a problem here. There
is never
the need to extract a complete standalone copy of a transaction’s history.
The Bitcoin Whitepaper by Satoshi Nakamoto
|
311
Privacy
The traditional banking model achieves a level of privacy by limiting
access to infor‐
mation to the parties involved and the trusted third party. The necessity
to announce
all transactions publicly precludes this method, but privacy can still be
maintained by
breaking the flow of information in another place: by keeping public keys
anony‐
mous. The public can see that someone is sending an amount to someone
else, but
without information linking the transaction to anyone. This is similar to
the level of
information released by stock exchanges, where the time and size of
individual
trades, the “tape”, is made public, but without telling who the parties
were.
As an additional firewall, a new key pair should be used for each
transaction to keep
them from being linked to a common owner. Some linking is still
unavoidable with
multi-input transactions, which necessarily reveal that their inputs were
owned by the
same owner. The risk is that if the owner of a key is revealed, linking
could reveal
other transactions that belonged to the same owner.
Calculations
We consider the scenario of an attacker trying to generate an alternate
chain faster
than the honest chain. Even if this is accomplished, it does not throw the
system open
to arbitrary changes, such as creating value out of thin air or taking
money that never
belonged to the attacker. Nodes are not going to accept an invalid
transaction as pay‐
ment, and honest nodes will never accept a block containing them. An
attacker can
only try to change one of his own transactions to take back money he
recently spent.
The race between the honest chain and an attacker chain can be
characterized as a
Binomial Random Walk. The success event is the honest chain being extended
by one
block, increasing its lead by +1, and the failure event is the attacker’s
chain being
extended by one block, reducing the gap by -1.
The probability of an attacker catching up from a given deficit is
analogous to a
Gambler’s Ruin problem. Suppose a gambler with unlimited credit starts at
a deficit
and plays potentially an infinite number of trials to try to reach
breakeven. We can
312
|
Appendix A: The Bitcoin Whitepaper by Satoshi Nakamoto
calculate the probability he ever reaches breakeven, or that an attacker
ever catches
up with the honest chain, as follows [8]:
p == probability an honest node finds the next block
q == probability the attacker finds the next block
qz == probability the attacker will ever catch up from z blocks behind
Given our assumption that p > q, the probability drops exponentially as
the number
of blocks the attacker has to catch up with increases. With the odds
against him, if he
doesn’t make a lucky lunge forward early on, his chances become
vanishingly small as
he falls further behind.
We now consider how long the recipient of a new transaction needs to wait
before
being sufficiently certain the sender can’t change the transaction. We
assume the
sender is an attacker who wants to make the recipient believe he paid him
for a while,
then switch it to pay back to himself after some time has passed. The
receiver will be
alerted when that happens, but the sender hopes it will be too late.
The receiver generates a new key pair and gives the public key to the
sender shortly
before signing. This prevents the sender from preparing a chain of blocks
ahead of
time by working on it continuously until he is lucky enough to get far
enough ahead,
then executing the transaction at that moment. Once the transaction is
sent, the dis‐
honest sender starts working in secret on a parallel chain containing an
alternate ver‐
sion of his transaction.
The recipient waits until the transaction has been added to a block and z
blocks have
been linked after it. He doesn’t know the exact amount of progress the
attacker has
made, but assuming the honest blocks took the average expected time per
block, the
attacker’s potential progress will be a Poisson distribution with expected
value:
To get the probability the attacker could still catch up now, we multiply
the Poisson
density for each amount of progress he could have made by the probability
he could
catch up from that point:
The Bitcoin Whitepaper by Satoshi Nakamoto
|
313
Rearranging to avoid summing the infinite tail of the distribution...
Converting to C code...
#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
double p == 1.0 - q;
double lambda == z * (q / p);
double sum == 1.0;
int i, k;
for (k == 0; k <== z; k++)
{
double poisson == exp(-lambda);
for (i == 1; i <== k; i++)
poisson *== lambda / i;
sum -== poisson * (1 - pow(q / p, z - k));
}
return sum;
}
Running some results, we can see the probability drop off exponentially
with z.
q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
314
|
Appendix A: The Bitcoin Whitepaper by Satoshi Nakamoto
z=30
z=35
z=40
z=45
z=50
P=0.0001522
P=0.0000379
P=0.0000095
P=0.0000024
P=0.0000006
Solving for P less than 0.1%...
P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340
Conclusion
We have proposed a system for electronic transactions without relying on
trust. We
started with the usual framework of coins made from digital signatures,
which pro‐
vides strong control of ownership, but is incomplete without a way to
prevent double-
spending. To solve this, we proposed a peer-to-peer network using
proof-of-work to
record a public history of transactions that quickly becomes
computationally imprac‐
tical for an attacker to change if honest nodes control a majority of CPU
power. The
network is robust in its unstructured simplicity. Nodes work all at once
with little
coordination. They do not need to be identified, since messages are not
routed to any
particular place and only need to be delivered on a best effort basis.
Nodes can leave
and rejoin the network at will, accepting the proof-of-work chain as proof
of what
happened while they were gone. They vote with their CPU power, expressing
their
acceptance of valid blocks by working on extending them and rejecting
invalid blocks
by refusing to work on them. Any needed rules and incentives can be
enforced with
this consensus mechanism.
References
[1] W. Dai, “b-money,” http://www.weidai.com/bmoney.txt, 1998.
[2] H. Massias, X.S. Avila, and J.-J. Quisquater, “Design of a secure
timestamping ser‐
vice with minimal trust requirements,” In 20th Symposium on Information
Theory in
the Benelux, May 1999.
[3] S. Haber, W.S. Stornetta, “How to time-stamp a digital document,” In
Journal of
Cryptology, vol 3, no 2, pages 99-111, 1991.
The Bitcoin Whitepaper by Satoshi Nakamoto
|
315
[4] D. Bayer, S. Haber, W.S. Stornetta, “Improving the efficiency and
reliability of dig‐
ital time-stamping,” In Sequences II: Methods in Communication, Security
and Com‐
puter Science, pages 329-334, 1993.
[5] S. Haber, W.S. Stornetta, “Secure names for bit-strings,” In
Proceedings of the 4th
ACM Conference on Computer and Communications Security, pages 28-35, April
1997.
[6] A. Back, “Hashcash - a denial of service counter-measure,”
http://www.hash‐
cash.org/papers/hashcash.pdf, 2002.
[7] R.C. Merkle, “Protocols for public key cryptosystems,” In Proc. 1980
Symposium
on Security and Privacy, IEEE Computer Society, pages 122-133, April 1980.
[8] W. Feller, “An introduction to probability theory and its
applications,” 1957.
License
This whitepaper was published in October 2008 by Satoshi Nakamoto. It was
later
(2009) added as supporting documentation to the bitcoin software and
carries the
same MIT license. It has been reproduced in this book, without
modification other
than formatting, under the terms of the MIT license:
The MIT License (MIT) Copyright (c) 2008 Satoshi Nakamoto
Permission is hereby granted, free of charge, to any person obtaining a
copy of this
software and associated documentation files (the “Software”), to deal in
the Software
without restriction, including without limitation the rights to use, copy,
modify,
merge, publish, distribute, sublicense, and/or sell copies of the
Software, and to per‐
mit persons to whom the Software is furnished to do so, subject to the
following con‐
ditions:
The above copyright notice and this permission notice shall be included in
all copies
or substantial portions of the Software.
THE SOFTWARE IS PROVIDED “AS IS,” WITHOUT WARRANTY OF ANY KIND,
EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRAN‐
TIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND
NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT
HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY,
WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE
OR OTHER DEALINGS IN THE SOFTWARE.
316
|
Appendix A: The Bitcoin Whitepaper by Satoshi Nakamoto
APPENDIX B
Transaction Script Language Operators,
Constants, and Symbols
Tables and descriptions sourced from https://en.bitcoin.it/wiki/
Script.
Table B-1 shows operators for pushing values onto the stack.
Table B-1. Push value onto stack
Symbol
Value (hex)
Description
OP_0 or OP_FALSE 0x00
An empty array is pushed onto the stack
1-75
0x01-0x4b
Push the next N bytes onto the stack, where N is 1 to 75 bytes
OP_PUSHDATA1
0x4c
The next script byte contains N, push the following N bytes onto the
stack
OP_PUSHDATA2
0x4d
The next two script bytes contain N, push the following N bytes onto
the stack
OP_PUSHDATA4
0x4e
The next four script bytes contain N, push the following N bytes
onto the stack
OP_1NEGATE
0x4f
Push the value “–1” onto the stack
OP_RESERVED
0x50
Halt - Invalid transaction unless found in an unexecuted OP_IF
clause
OP_1 or OP_TRUE
0x51
Push the value “1” onto the stack
OP_2 to OP_16
0x52 to 0x60 For OP_N, push the value “N” onto the stack, e.g., OP_2
pushes “2”
317
Table B-2 shows conditional flow control operators.
Table B-2. Conditional flow control
Symbol
Value (hex) Description
OP_NOP
0x61
Do nothing
OP_VER
0x62
Halt—Invalid transaction unless found in an unexecuted OP_IF clause
OP_IF
0x63
Execute the statements following if top of stack is not 0
OP_NOTIF
0x64
Execute the statements following if top of stack is 0
OP_VERIF
0x65
Halt—Invalid transaction
OP_VERNOTIF 0x66
Halt—Invalid transaction
OP_ELSE
0x67
Execute only if the previous statements were not executed
OP_ENDIF
0x68
End the OP_IF, OP_NOTIF, OP_ELSE block
OP_VERIFY
0x69
Check the top of the stack, halt and invalidate transaction if not
TRUE
OP_RETURN
0x6a
Halt and invalidate transaction
Table B-3 shows operators used for timelocks.
Table B-3. Timelock operations
Symbol
OP_CHECKLOCKTIMEVERIFY
(previously OP_NOP2)
OP_CHECKSEQUENCEVERIFY
(previously OP_NOP3)
Value
(hex)
0xb1
0xb2
Description
Marks transaction as invalid if the top stack item is greater than the
transaction’s
nLockTime field, otherwise script evaluation continues as though an OP_NOP
was
executed. Transaction is also invalid if 1. the stack is empty; or 2. the
top stack
item is negative; or 3. the top stack item is greater than or equal to
500000000
while the transaction’s nLockTime field is less than 500000000, or vice
versa; or 4.
the input’s nSequence field is equal to 0xffffffff. The precise semantics
are
described in BIP-65
Marks transaction as invalid if the relative lock time of the input
(enforced by BIP
0068 with nSequence) is not equal to or longer than the value of the top
stack
item. The precise semantics are described in BIP-112
Table B-4 shows operators used to manipulate the stack.
Table B-4. Stack operations
Symbol
Value (hex) Description
OP_TOALTSTACK
0x6b
Pop top item from stack and push to alternative stack
OP_FROMALTSTACK 0x6c
Pop top item from alternative stack and push to stack
OP_2DROP
0x6d
Pop top two stack items
OP_2DUP
0x6e
Duplicate top two stack items
OP_3DUP
0x6f
Duplicate top three stack items
OP_2OVER
0x70
Copy the third and fourth items in the stack to the top
318
|
Appendix B: Transaction Script Language Operators, Constants, and
Symbols
Symbol
OP_2ROT
OP_2SWAP
OP_IFDUP
OP_DEPTH
OP_DROP
OP_DUP
OP_NIP
OP_OVER
OP_PICK
OP_ROLL
OP_ROT
OP_SWAP
OP_TUCK
Value0x71
0x72
0x73
0x74
0x75
0x76
0x77
0x78
0x79
0x7a
0x7b
0x7c
0x7d
(hex)Description
Move the fifth and sixth items in the stack to the top
Swap the two top pairs of items in the stack
Duplicate the top item in the stack if it is not 0
Count the items on the stack and push the resulting count
Pop the top item in the stack
Duplicate the top item in the stack
Pop the second item in the stack
Copy the second item in the stack and push it onto the top
Pop value N from top, then copy the Nth item to the top of the stack
Pop value N from top, then move the Nth item to the top of the stack
Rotate the top three items in the stack
Swap the top three items in the stack
Copy the top item and insert it between the top and second item.
Table B-5 shows string operators.
Table B-5. String splice operations
Symbol
Value (hex) Description
OP_CAT
0x7e
Disabled (concatenates top two items)
OP_SUBSTR 0x7f
Disabled (returns substring)
OP_LEFT
0x80
Disabled (returns left substring)
OP_RIGHT
0x81
Disabled (returns right substring)
OP_SIZE
0x82
Calculate string length of top item and push the result
Table B-6 shows binary arithmetic and boolean logic operators.
Table B-6. Binary arithmetic and conditionals
Symbol
Value (hex) Description
OP_INVERT
0x83
Disabled (Flip the bits of the top item)
OP_AND
0x84
Disabled (Boolean AND of two top items)
OP_OR
0x85
Disabled (Boolean OR of two top items)
OP_XOR
0x86
Disabled (Boolean XOR of two top items)
OP_EQUAL
0x87
Push TRUE (1) if top two items are exactly equal, push FALSE (0)
otherwise
OP_EQUALVERIFY 0x88
Same as OP_EQUAL, but run OP_VERIFY after to halt if not TRUE
OP_RESERVED1
0x89
Halt - Invalid transaction unless found in an unexecuted OP_IF
clause
OP_RESERVED2
0x8a
Halt - Invalid transaction unless found in an unexecuted OP_IF
clause
Transaction Script Language Operators, Constants, and Symbols
|
319
Table B-7 shows numeric (arithmetic)Table B-7. Numeric operators
Symbol
OP_1ADD
OP_1SUB
OP_2MUL
OP_2DIV
OP_NEGATE
OP_ABS
OP_NOT
OP_0NOTEQUAL
OP_ADD
OP_SUB
OP_MUL
OP_DIV
OP_MOD
OP_LSHIFT
OP_RSHIFT
OP_BOOLAND
OP_BOOLOR
OP_NUMEQUAL
OP_NUMEQUALVERIFY
OP_NUMNOTEQUAL
OP_LESSTHAN
OP_GREATERTHAN
OP_LESSTHANOREQUAL
OP_GREATERTHANOREQUALOP_MIN
OP_MAX
OP_WITHIN
Value
(hex)
0x8b
0x8c
0x8d
0x8e
0x8f
0x90
0x91
0x92
0x93
0x94
0x95
0x96
0x97
0x98
0x99
0x9a
0x9b
0x9c
0x9d
0x9e
0x9f
0xa0
0xa1
0xa2
0xa3
0xa4
0xa5
operators.
Description
Add 1 to the top item
Subtract 1 from the top item
Disabled (multiply top item by 2)
Disabled (divide top item by 2)
Flip the sign of top item
Change the sign of the top item to positive
If top item is 0 or 1 Boolean flip it, otherwise return 0
If top item is 0 return 0, otherwise return 1
Pop top two items, add them and push result
Pop top two items, subtract first from second, push result
Disabled (multiply top two items)
Disabled (divide second item by first item)
Disabled (remainder divide second item by first item)
Disabled (shift second item left by first item number of bits)
Disabled (shift second item right by first item number of bits)
Boolean AND of top two items
Boolean OR of top two items
Return TRUE if top two items are equal numbers
Same as NUMEQUAL, then OP_VERIFY to halt if not TRUE
Return TRUE if top two items are not equal numbers
Return TRUE if second item is less than top item
Return TRUE if second item is greater than top item
Return TRUE if second item is less than or equal to top item
Return TRUE if second item is great than or equal to top item
Return the smaller of the two top items
Return the larger of the two top items
Return TRUE if the third item is between the second item (or equal) and
first item
320
|
Appendix B: Transaction Script Language Operators, Constants, and
Symbols
Table B-8 shows cryptographic function operators.
Table B-8. Cryptographic and hashing operations
Symbol
Value
Description
(hex)
OP_RIPEMD160
0xa6
Return RIPEMD160 hash of top item
OP_SHA1
0xa7
Return SHA1 hash of top item
OP_SHA256
0xa8
Return SHA256 hash of top item
OP_HASH160
0xa9
Return RIPEMD160(SHA256(x)) hash of top item
OP_HASH256
0xaa
Return SHA256(SHA256(x)) hash of top item
OP_CODESEPARATOR
0xab
Mark the beginning of signature-checked data
OP_CHECKSIG
0xac
Pop a public key and signature and validate the signature for the
transaction’s
hashed data, return TRUE if matching
OP_CHECKSIGVERIFY
0xad
Same as CHECKSIG, then OP_VERIFY to halt if not TRUE
OP_CHECKMULTISIG
0xae
Run CHECKSIG for each pair of signature and public key provided. All
must match.
Bug in implementation pops an extra value, prefix with OP_NOP as
workaround
OP_CHECKMULTISIGVERIFY 0xaf
Same as CHECKMULTISIG, then OP_VERIFY to halt if not TRUE
Table B-9 shows nonoperator symbols.
Table B-9. Nonoperators
Symbol
Value (hex) Description
OP_NOP1-OP_NOP10 0xb0-0xb9 Does nothing, ignored
Table B-10 shows operator codes reserved for use by the internal script
parser.
Table B-10. Reserved OP codes for internal use by the parser
Symbol
Value (hex) Description
OP_SMALLDATA
0xf9
Represents small data field
OP_SMALLINTEGER
0xfa
Represents small integer data field
OP_PUBKEYS
0xfb
Represents public key fields
OP_PUBKEYHASH
0xfd
Represents a public key hash field
OP_PUBKEY
0xfe
Represents a public key field
OP_INVALIDOPCODE 0xff
Represents any OP code not currently assigned
Transaction Script Language Operators, Constants, and Symbols
|
321
APPENDIX C
Bitcoin Improvement Proposals
Bitcoin Improvement Proposals are design documents providing information
to the
bitcoin community, or for describing a new feature for bitcoin or its
processes or
environment.
As per BIP-01 BIP Purpose and Guidelines, there are three kinds of BIPs:
Standard BIP
Describes any change that affects most or all bitcoin implementations,
such as a
change to the network protocol, a change in block or transaction validity
rules, or
any change or addition that affects the interoperability of applications
using bit‐
coin.
Informational BIP
Describes a bitcoin design issue, or provides general guidelines or
information to
the bitcoin community, but does not propose a new feature. Informational
BIPs
do not necessarily represent a bitcoin community consensus or
recommendation,
so users and implementors may ignore informational BIPs or follow their
advice.
Process BIP
Describes a bitcoin process, or proposes a change to (or an event in) a
process.
Process BIPs are like standard BIPs but apply to areas other than the
bitcoin pro‐
tocol itself. They might propose an implementation, but not to bitcoin’s
codebase;
they often require community consensus; and unlike informational BIPs,
they are
more than recommendations, and users are typically not free to ignore
them.
Examples include procedures, guidelines, changes to the decision-making
pro‐
cess, and changes to the tools or environment used in bitcoin development.
Any
meta-BIP is also considered a process BIP.
323
BIPs are recorded in a versioned repository on GitHub:
https://github.com/bitcoin/
bips. Table C-1 shows a snapshot of the BIPs in April 2017. Consult the
authoritative
repository for up-to-date information on existing BIPs and their contents.
Table C-1. Snapshot of BIPs
BIP#
Title
BIP-1
BIP Purpose and Guidelines
BIP-2
BIP process, revised
BIP-8
Version bits with guaranteed lock-in
BIP-9
Version bits with timeout and delay
BIP-10
BIP-11
BIP-12
BIP-13
BIP-14
Multi-Sig Transaction Distribution
M-of-N Standard Transactions
OP_EVAL
Address Format for pay-to-script-hash
Protocol Version and User Agent
BIP-15
BIP-16
BIP-17
BIP-18
BIP-19
BIP-20
BIP-21
Aliases
Pay to Script Hash
OP_CHECKHASHVERIFY (CHV)
hashScriptCheck
M-of-N Standard Transactions (Low SigOp)
URI Scheme
URI Scheme
BIP-22
BIP-23
BIP-30
BIP-31
BIP-32
BIP-33
BIP-34
BIP-35
BIP-36
BIP-37
BIP-38
getblocktemplate - Fundamentals
getblocktemplate - Pooled Mining
Duplicate transactions
Pong message
Hierarchical Deterministic Wallets
Stratized Nodes
Block v2, Height in Coinbase
mempool message
Custom Services
Connection Bloom filtering
Passphrase-protected private key
BIP-39
Mnemonic code for generating deterministic keys
Owner
Type
Status
Amir Taaki
Process
Replaced
Luke Dashjr
Process
Active
Shaolin Fry
Informational Draft
Pieter Wuille, Peter Todd,
Informational Final
Greg Maxwell, Rusty
Russell
Alan Reiner
Informational Withdrawn
Gavin Andresen
Standard
Final
Gavin Andresen
Standard
Withdrawn
Gavin Andresen
Standard
Final
Amir Taaki, Patrick
Standard
Final
Strateman
Amir Taaki
Standard
Deferred
Gavin Andresen
Standard
Final
Luke Dashjr
Standard
Withdrawn
Luke Dashjr
Standard
Proposed
Luke Dashjr
Standard
Draft
Luke Dashjr
Standard
Replaced
Nils Schneider, Matt
Standard
Final
Corallo
Luke Dashjr
Standard
Final
Luke Dashjr
Standard
Final
Pieter Wuille
Standard
Final
Mike Hearn
Standard
Final
Pieter Wuille
Informational Final
Amir Taaki
Standard
Draft
Gavin Andresen
Standard
Final
Jeff Garzik
Standard
Final
Stefan Thomas
Standard
Draft
Mike Hearn, Matt Corallo
Standard
Final
Mike Caldwell, Aaron
Standard
Draft
Voisine
Marek Palatinus, Pavol
Standard
Proposed
Rusnak, Aaron Voisine,
Sean Bowe
324
|
Appendix C: Bitcoin Improvement Proposals
BIP#
Title
Owner
Type
Status
BIP-40
Stratum wire protocol
Marek Palatinus
Standard
BIP number
allocated
BIP-41
Stratum mining protocol
Marek Palatinus
Standard
BIP number
allocated
BIP-42
A finite monetary supply for Bitcoin
Pieter Wuille
Standard
Draft
BIP-43
Purpose Field for Deterministic Wallets
Marek Palatinus, Pavol
Informational Draft
Rusnak
BIP-44
Multi-Account Hierarchy for Deterministic Wallets
Marek Palatinus, Pavol
Standard
Proposed
Rusnak
BIP-45
Structure for Deterministic P2SH Multisignature
Manuel Araoz, Ryan X.
Standard
Proposed
Wallets
Charles, Matias Alejo Garcia
BIP-47
Reusable Payment Codes for Hierarchical
Justus Ranvier
Informational Draft
Deterministic Wallets
BIP-49
Derivation scheme for P2WPKH-nested-in-P2SH
Daniel Weigl
Informational Draft
based accounts
BIP-50
March 2013 Chain Fork Post-Mortem
Gavin Andresen
Informational Final
BIP-60
Fixed Length “version” Message (Relay-Transactions Amir Taaki
Standard
Draft
Field)
BIP-61
Reject P2P message
Gavin Andresen
Standard
Final
BIP-62
Dealing with malleability
Pieter Wuille
Standard
Withdrawn
BIP-63
Stealth Addresses
Peter Todd
Standard
BIP number
allocated
BIP-64
getutxo message
Mike Hearn
Standard
Draft
BIP-65
OP_CHECKLOCKTIMEVERIFY
Peter Todd
Standard
Final
BIP-66
Strict DER signatures
Pieter Wuille
Standard
Final
BIP-67
Deterministic Pay-to-script-hash multi-signature
Thomas Kerin, Jean-Pierre
Standard
Proposed
addresses through public key sorting
Rupp, Ruben de Vries
BIP-68
Relative lock-time using consensus-enforced
Mark Friedenbach, BtcDrak, Standard
Final
sequence numbers
Nicolas Dorier,
kinoshitajona
BIP-69
Lexicographical Indexing of Transaction Inputs and
Kristov Atlas
Informational Proposed
Outputs
BIP-70
Payment Protocol
Gavin Andresen, Mike
Standard
Final
Hearn
BIP-71
Payment Protocol MIME types
Gavin Andresen
Standard
Final
BIP-72
bitcoin: uri extensions for Payment Protocol
Gavin Andresen
Standard
Final
BIP-73
Use “Accept” header for response type negotiation
Stephen Pair
Standard
Final
with Payment Request URLs
BIP-74
Allow zero value OP_RETURN in Payment Protocol
Toby Padilla
Standard
Draft
BIP-75
Out of Band Address Exchange using Payment
Justin Newton, Matt David, Standard
Draft
Protocol Encryption
Aaron Voisine, James
MacWhyte
Bitcoin Improvement Proposals
|
325
BIP#
BIP-80
BIP-81
BIP-83
BIP-90
BIP-99
BIP-101BIP-102BIP-103BIP-104BIP-105BIP-106BIP-107BIP-109BIP-111BIP-112Title
Hierarchy for Non-Colored Voting Pool DeterministicMultisig Wallets
Hierarchy for Colored Voting Pool Deterministic
Multisig Wallets
Dynamic Hierarchical Deterministic Key Trees
Buried Deployments
Motivation and deployment of consensus rule
changes ([soft/hard]forks)
Increase maximum block size
Block size increase to 2MB
Block size following technological growth
Block75 - Max block size like difficulty
Consensus based block size retargeting algorithm
Dynamically Controlled Bitcoin Block Size Max Cap
Dynamic limit on the block size
Two million byte size limit with sigop and sighash
limits
NODE_BLOOM service bit
CHECKSEQUENCEVERIFY
BIP-113BIP-114BIP-120BIP-121BIP-122BIP-123BIP-124Median time-past as
endpoint for lock-time
calculations
Merkelized Abstract Syntax Tree
Proof of Payment
Proof of Payment URI scheme
URI scheme for Blockchain references / exploration
BIP Classification
Hierarchical Deterministic Script Templates
BIP-125 Opt-in Full Replace-by-Fee Signaling
BIP-126BIP-130BIP-131BIP-132BIP-133BIP-134BIP-140Best Practices for
Heterogeneous Input Script
Transactions
sendheaders message
“Coalescing Transaction” Specification (wildcard
inputs)
Committee-based BIP Acceptance Process
feefilter message
Flexible Transactions
Normalized TXID
Owner
Justus Ranvier, Jimmy
Song
Justus Ranvier, Jimmy
Song
Eric Lombrozo
Suhas Daftuar
Jorge Timón
Gavin Andresen
Jeff Garzik
Pieter Wuille
t.khan
BtcDrak
Upal Chakraborty
Washington Y. Sanchez
Gavin Andresen
Matt Corallo, Peter Todd
BtcDrak, Mark Friedenbach,Eric Lombrozo
Thomas Kerin, Mark
Friedenbach
Johnson Lau
Kalle Rosenbaum
Kalle Rosenbaum
Marco Pontello
Eric Lombrozo
Eric Lombrozo, William
Swanson
David A. Harding, Peter
Todd
Kristov Atlas
Suhas Daftuar
Chris Priest
Andy Chase
Alex Morcos
Tom Zander
Christian Decker
Type
InformationalStatus
Deferred
Informational Deferred
Standard
InformationalInformationalDraft
Draft
Draft
Standard
Standard
Standard
Standard
Standard
Standard
Standard
Standard
Withdrawn
Draft
Draft
Draft
Draft
Draft
Draft
Rejected
Standard
Standard
Standard
Standard
Standard
Standard
Standard
Process
InformationalStandard
InformationalStandard
Standard
Process
Standard
Standard
Standard
Proposed
Final
Final
Draft
Draft
Draft
Draft
Active
Draft
Proposed
Draft
Proposed
Draft
Withdrawn
Draft
Draft
Draft
326
|
Appendix C: Bitcoin Improvement Proposals
BIP#
BIP-141Title
Segregated Witness (Consensus layer)
BIP-142BIP-143BIP-144Address Format for Segregated Witness
Transaction Signature Verification for Version 0
Witness Program
Segregated Witness (Peer Services)
BIP-145BIP-146BIP-147BIP-148BIP-150BIP-151BIP-152BIP-171BIP-180BIP-199getblocktemplate
Updates for Segregated Witness
Dealing with signature encoding malleability
Dealing with dummy stack element malleability
Mandatory activation of segwit deployment
Peer Authentication
Peer-to-Peer Communication Encryption
Compact Block Relay
Currency/exchange rate information API
Block size/weight fraud proof
Hashed Time-Locked Contract transactions
Owner
Eric Lombrozo, Johnson
Lau, Pieter Wuille
Johnson Lau
Johnson Lau, Pieter Wuille
Type
Standard
Standard
Standard
Eric Lombrozo, Pieter
Wuille
Luke Dashjr
Johnson Lau, Pieter Wuille
Johnson Lau
Shaolin Fry
Jonas Schnelli
Jonas Schnelli
Matt Corallo
Luke Dashjr
Luke Dashjr
Sean Bowe, Daira
Hopwood
Standard
Standard
Standard
Standard
Standard
Standard
Standard
Standard
Standard
Standard
Standard
Status
Draft
Deferred
Draft
Draft
Draft
Draft
Draft
Draft
Draft
Draft
Draft
Draft
Draft
Draft
Bitcoin Improvement Proposals
|
327
SegregatedAPPENDIX D
Witness
Segregated Witness (segwit) is an upgrade to the bitcoin consensus rules
and network
protocol, proposed and implemented as a BIP-9 soft-fork that is currently
(mid-2017)
pending activation.
In cryptography, the term “witness” is used to describe a solution to a
cryptographic
puzzle. In bitcoin terms, the witness satisfies a cryptographic condition
placed on a
unspent transaction output (UTXO).
In the context of bitcoin, a digital signature is one type of witness, but
a witness is
more broadly any solution that can satisfy the conditions imposed on an
UTXO and
unlock that UTXO for spending. The term “witness” is a more general term
for an
“unlocking script” or “scriptSig.”
Before segwit’s introduction, every input in a transaction was followed by
the witness
data that unlocked it. The witness data was embedded in the transaction as
part of
each input. The term segregated witness, or segwit for short, simply means
separating
the signature or unlocking script of a specific output. Think “separate
scriptSig,” or
“separate signature” in the simplest form.
Segregated Witness therefore is an architectural change to bitcoin that
aims to move
the witness data from the scriptSig (unlocking script) field of a
transaction into a
separate witness data structure that accompanies a transaction. Clients
may request
transaction data with or without the accompanying witness data.
In this section we will look at some of the benefits of Segregated
Witness, describe the
mechanism used to deploy and implement this architecture change, and
demonstrate
the use of Segregated Witness in transactions and addresses.
329
Segregated Witness is defined by the following BIPs:
BIP-141
The main definition of Segregated Witness.
BIP-143
Transaction Signature Verification for Version 0 Witness Program
BIP-144
Peer Services—New network messages and serialization formats
BIP-145
getblocktemplate Updates for Segregated Witness (for mining)
Why Segregated Witness?
Segregated Witness is an architectural change that has several effects on
the scalabil‐
ity, security, economic incentives, and performance of bitcoin:
Transaction Malleability
By moving the witness outside the transaction, the transaction hash used
as an
identifier no longer includes the witness data. Since the witness data is
the only
part of the transaction that can be modified by a third party (see
“Transaction
identifiers” on page 338), removing it also removes the opportunity for
transac‐
tion malleability attacks. With Segregated Witness, transaction hashes
become
immutable by anyone other than the creator of the transaction, which
greatly
improves the implementation of many other protocols that rely on advanced
bit‐
coin transaction construction, such as payment channels, chained
transactions,
and lightning networks.
Script Versioning
With the introduction of Segregated Witness scripts, every locking script
is pre‐
ceded by a script version number, similar to how transactions and blocks
have
version numbers. The addition of a script version number allows the
scripting
language to be upgraded in a backward-compatible way (i.e., using soft
fork
upgrades) to introduce new script operands, syntax, or semantics. The
ability to
upgrade the scripting language in a nondisruptive way will greatly
accelerate the
rate of innovation in bitcoin.
Network and Storage Scaling
The witness data is often a big contributor to the total size of a
transaction. More
complex scripts such as those used for multisig or payment channels are
very
large. In some cases these scripts account for the majority (more than
75%) of the
data in a transaction. By moving the witness data outside the transaction,
Segre‐
gated Witness improves bitcoin’s scalability. Nodes can prune the witness
data
after validating the signatures, or ignore it altogether when doing
simplified pay‐
330
|
Appendix D: Segregated Witness
ment verification. The witness data doesn’t need to be transmitted to all
nodes
and does not need to be stored on disk by all nodes.
Signature Verification Optimization
Segregated Witness upgrades the signature functions (CHECKSIG,
CHECKMULTISIG,
etc.) to reduce the algorithm’s computational complexity. Before segwit,
the algo‐
rithm used to produce a signature required a number of hash operations
that was
proportional to the size of the transaction. Data-hashing computations
increased
in O(n2) with respect to the number of signature operations, introducing a
sub‐
stantial computational burden on all nodes verifying the signature. With
segwit,
the algorithm is changed to reduce the complexity to O(n).
Offline Signing Improvement
Segregated Witness signatures incorporate the value (amount) referenced by
each
input in the hash that is signed. Previously, an offline signing device,
such as a
hardware wallet, would have to verify the amount of each input before
signing a
transaction. This was usually accomplished by streaming a large amount of
data
about the previous transactions referenced as inputs. Since the amount is
now
part of the commitment hash that is signed, an offline device does not
need the
previous transactions. If the amounts do not match (are misrepresented by
a
compromised online system), the signature will be invalid.
How Segregated Witness Works
At first glance, Segregated Witness appears to be a change to how
transactions are
constructed and therefore a transaction-level feature, but it is not. In
fact, Segregated
Witness is also a change to how individual UTXO are spent and therefore is
a per-
output feature.
A transaction can spend Segregated Witness outputs or traditional
(inline-witness)
outputs or both. Therefore, it does not make much sense to refer to a
transaction as a
“Segregated Witness transaction.” Rather we should refer to specific
transaction
inputs as “Segregated Witness inputs.”
When a transaction spends an UTXO, it must provide a witness. In a
traditional
UTXO, the locking script requires that witness data be provided inline in
the input
part of the transaction that spends the UTXO. A Segregated Witness UTXO,
however,
specifies a locking script that can be satisfied with witness data outside
of the input
(segregated).
Soft Fork (Backward Compatibility)
Segregated Witness is a significant change to the way outputs and
transactions are
architected. Such a change would normally require a simultaneous change in
every
bitcoin node and wallet to change the consensus rules—what is known as a
hard fork.
Segregated Witness
|
331
Instead, segregated witness is introduced with a much less disruptive
change, which is
backward compatible, known as a soft fork. This type of upgrade allows
nonupgraded
software to ignore the changes and continue to operate without any
disruption.
Segregated Witness outputs are constructed so that older systems that are
not segwit-
aware can still validate them. To an old wallet or node, a Segregated
Witness output
looks like an output that anyone can spend. Such outputs can be spent with
an empty
signature, therefore the fact that there is no signature inside the
transaction (it is seg‐
regated) does not invalidate the transaction. Newer wallets and mining
nodes, how‐
ever, see the Segregated Witness output and expect to find a valid witness
for it in the
transaction’s witness data.
Segregated Witness Output and Transaction Examples
Let’s look at some of our example transactions and see how they would
change with
Segregated Witness. We’ll first look at how a Pay-to-Public-Key-Hash
(P2PKH) pay‐
ment is transformed with the Segregated Witness program. Then, we’ll look
at the
Segregated Witness equivalent for Pay-to-Script-Hash (P2SH) scripts.
Finally, we’ll
look at how both of the preceding Segregated Witness programs can be
embedded
inside a P2SH script.
Pay-to-Witness-Public-Key-Hash (P2WPKH)
In “Buying a Cup of Coffee” on page 16, Alice created a transaction to pay
Bob for a
cup of coffee. That transaction created a P2PKH output with a value of
0.015 BTC
that was spendable by Bob. The output’s script looks like this:
DUP HASH160 ab68025513c3dbd2f7b92a94e0581f5d50f654e7 EQUALVERIFY CHECKSIG
With Segregated Witness, Alice would create a
Pay-to-Witness-Public-Key-Hash
(P2WPKH) script, which looks like this:
0 ab68025513c3dbd2f7b92a94e0581f5d50f654e7
As you can see, a Segregated Witness output’s locking script is much
simpler than a
traditional output. It consists of two values that are pushed on to the
script evaluation
stack. To an old (nonsegwit-aware) bitcoin client, the two pushes would
look like an
output that anyone can spend and does not require a signature (or rather,
can be
spent with an empty signature). To a newer, segwit-aware client, the first
number (0)
is interpreted as a version number (the witness version) and the second
part (20 bytes)
is the equivalent of a locking script known as a witness program. The
20-byte witness
program is simply the hash of the public key, as in a P2PKH script
Now, let’s look at the corresponding transaction that Bob uses to spend
this output.
For the original script (nonsegwit), Bob’s transaction would have to
include a signa‐
ture within the transaction input:
332
|
Appendix D: Segregated Witness
[...]
“Vin” : [
"txid":
"0627052b6f28912f2703066a912ea577f2ce4da4caa5a5fbd8a57286c345c2f2",
"vout": 0,
"scriptSig": “<Bob’s scriptSig>”,
]
[...]
However, to spend the Segregated Witness output, the transaction has no
signature
on that input. Instead, Bob’s transaction has an empty scriptSig and
includes a Seg‐
regated Witness, outside the transaction itself:
[...]
“Vin” : [
"txid":
"0627052b6f28912f2703066a912ea577f2ce4da4caa5a5fbd8a57286c345c2f2",
"vout": 0,
"scriptSig": “”,
]
[...]
“witness”: “<Bob’s witness data>”
[...]
Wallet construction of P2WPKH
It is extremely important to note that P2WPKH should only be created by
the payee
(recipient) and not converted by the sender from a known public key, P2PKH
script,
or address. The sender has no way of knowing if the recipient’s wallet has
the ability
to construct segwit transactions and spend P2WPKH outputs.
Additionally, P2WPKH outputs must be constructed from the hash of a
compressed
public key. Uncompressed public keys are nonstandard in segwit and may be
explic‐
itly disabled by a future soft fork. If the hash used in the P2WPKH came
from an
uncompressed public key, it may be unspendable and you may lose funds.
P2WPKH
outputs should be created by the payee’s wallet by deriving a compressed
public key
from their private key.
P2WPKH should be constructed by the payee (recipient) by con‐
verting a compressed public key to a P2WPKH hash. You should
never transform a P2PKH script, bitcoin address, or uncompressed
public key to a P2WPKH witness script.
Pay-to-Witness-Script-Hash (P2WSH)
The second type of witness program corresponds to a Pay-to-Script-Hash
(P2SH)
script. We saw this type of script in “Pay-to-Script-Hash (P2SH)” on page
151. In that
example, P2SH was used by Mohammed’s company to express a multisignature
script. Payments to Mohammed’s company were encoded with a locking script
like
this:
Segregated Witness
|
333
HASH160 54c557e07dde5bb6cb791c7a540e0a4796f5e97e EQUAL
This P2SH script references the hash of a redeem script that defines a
2-of-3 multi‐
signature requirement to spend funds. To spend this output, Mohammed’s
company
would present the redeem script (whose hash matches the script hash in the
P2SH
output) and the signatures necessary to satisfy that redeem script, all
inside the trans‐
action input:
[...]
“Vin” : [
"txid": "abcdef12345...",
"vout": 0,
"scriptSig": “<SigA> <SigB> <2 PubA PubB PubC PubD PubE 5
CHECKMULTI-
SIG>”,
]
Now, let’s look at how this entire example would be upgraded to segwit. If
Moham‐
med’s customers were using a segwit-compatible wallet, they would make a
payment,
creating a Pay-to-Witness-Script-Hash (P2WSH) output that would look like
this:
0 9592d601848d04b172905e0ddb0adde59f1590f1e553ffc81ddc4b0ed927dd73
Again, as with the example of P2WPKH, you can see that the Segregated
Witness
equivalent script is a lot simpler and omits the various script operands
that you see in
P2SH scripts. Instead, the Segregated Witness program consists of two
values pushed
to the stack: a witness version (0) and the 32-byte SHA256 hash of the
redeem script.
While P2SH uses the 20-byte RIPEMD160(SHA256(script)) hash,
the P2WSH witness program uses a 32-byte SHA256(script) hash.
This difference in the selection of the hashing algorithm is deliber‐
ate and is used to differentiate between the two types of witness
programs (P2WPKH and P2WSH) by the length of the hash and to
provide stronger security to P2WSH (128 bits versus 80 bits of
P2SH).
Mohammed’s company can spend outputs the P2WSH output by presenting the
cor‐
rect redeem script and sufficient signatures to satisfy it. Both the
redeem script and
the signatures would be segregated outside the spending transaction as
part of the
witness data. Within the transaction input, Mohammed’s wallet would put an
empty
scriptSig:
[...]
“Vin” : [
"txid": "abcdef12345...",
"vout": 0,
"scriptSig": “”,
]
[...]
334
| Appendix D: Segregated Witness
“witness”: “<SigA> <SigB> <2 PubA PubB PubC PubD PubE 5
CHECKMULTISIG>”
[...]
Differentiating between P2WPKH and P2WSH
In the previous two sections, we demonstrated two types of witness
programs: “Pay-
to-Witness-Public-Key-Hash (P2WPKH)” on page 332 and
“Pay-to-Witness-Script-
Hash (P2WSH)” on page 333. Both types of witness programs consist of a
single byte
version number followed by a longer hash. They look very similar, but are
interpreted
very differently: one is interpreted as a public key hash, which is
satisfied by a signa‐
ture and the other as a script hash, which is satisfied by a redeem
script. The critical
difference between them is the length of the hash:
• The public key hash in P2WPKH is 20 bytes
• The script hash in P2WSH is 32 bytes
This is the one difference that allows a wallet to differentiate between
the two types of
witness programs. By looking at the length of the hash, a wallet can
determine what
type of witness program it is, P2WPKH or P2WSH.
Upgrading to Segregated Witness
As we can see from the previous examples, upgrading to Segregated Witness
is a two-
step process. First, wallets must create special segwit type outputs.
Then, these out‐
puts can be spent by wallets that know how to construct Segregated Witness
transactions. In the examples, Alice’s wallet was segwit-aware and able to
create spe‐
cial outputs with Segregated Witness scripts. Bob’s wallet is also
segwit-aware and
able to spend those outputs. What may not be obvious from the example is
that in
practice, Alice’s wallet needs to know that Bob uses a segwit-aware wallet
and can
spend these outputs. Otherwise, if Bob’s wallet is not upgraded and Alice
tries to
make segwit payments to Bob, Bob’s wallet will not be able to detect these
payments.
For P2WPKH and P2WSH payment types, both the sender and the
recipient wallets need to be upgraded to be able to use segwit. Fur‐
thermore, the sender’s wallet needs to know that the recipient’s wal‐
let is segwit-aware.
Segregated Witness will not be implemented simultaneously across the
entire net‐
work. Rather, Segregated Witness is implemented as a backward-compatible
upgrade,
where old and new clients can coexist. Wallet developers will
independently upgrade
wallet software to add segwit capabilities. The P2WPKH and P2WSH payment
types
are used when both sender and recipient are segwit-aware. The traditional
P2PKH
Segregated Witness
|
335
and P2SH will continue to work for nonupgraded wallets. That leaves two
important
scenarios, which are addressed in the next section:
• Ability of a sender’s wallet that is not segwit-aware to make a payment
to a recipi‐
ent’s wallet that can process segwit transactions
• Ability of a sender’s wallet that is segwit-aware to recognize and
distinguish
between recipients that are segwit-aware and ones that are not, by their
addresses
Embedding Segregated Witness inside P2SH
Let’s assume, for example, that Alice’s wallet is not upgraded to segwit,
but Bob’s wal‐
let is upgraded and can handle segwit transactions. Alice and Bob can use
“old” non-
segwit transactions. But Bob would likely want to use segwit to reduce
transaction
fees, taking advantage of the discount that applies to witness data.
In this case Bob’s wallet can construct a P2SH address that contains a
segwit script
inside it. Alice’s wallet sees this as a “normal” P2SH address and can
make payments
to it without any knowledge of segwit. Bob’s wallet can then spend this
payment with
a segwit transaction, taking full advantage of segwit and reducing
transaction fees.
Both forms of witness scripts, P2WPKH and P2WSH, can be embedded in a P2SH
address. The first is noted as P2SH(P2WPKH) and the second is noted as
P2SH(P2WSH).
Pay-to-Witness-Public-Key-Hash inside Pay-to-Script-Hash
The first form of witness script we will examine is P2SH(P2WPKH). This is
a Pay-to-
Witness-Public-Key-Hash witness program, embedded inside a
Pay-to-Script-Hash
script, so that it can be used by a wallet that is not aware of segwit.
Bob’s wallet constructs a P2WPKH witness program with Bob’s public key.
This wit‐
ness program is then hashed and the resulting hash is encoded as a P2SH
script. The
P2SH script is converted to a bitcoin address, one that starts with a “3,”
as we saw in
the “Pay-to-Script-Hash (P2SH)” on page 151 section.
Bob’s wallet starts with the P2WPKH witness program we saw earlier:
0 ab68025513c3dbd2f7b92a94e0581f5d50f654e7
The P2WPKH witness program consists of the witness version and Bob’s
20-byte
public key hash.
Bob’s wallet then hashes the preceding witness program, first with SHA256,
then with
RIPEMD160, producing another 20-byte hash:
3e0547268b3b19288b3adef9719ec8659f4b2b0b
336
|
Appendix D: Segregated Witness
The hash of the witness program is then embedded in a P2SH script:
HASH160 3e0547268b3b19288b3adef9719ec8659f4b2b0b EQUAL
Finally, the P2SH script is converted to a P2SH bitcoin address:
37Lx99uaGn5avKBxiW26HjedQE3LrDCZru
Now, Bob can display this address for customers to pay for their coffee.
Alice’s wallet
can make a payment to 37Lx99uaGn5avKBxiW26HjedQE3LrDCZru, just as it would
to
any other bitcoin address. Even though Alice’s wallet has no support for
segwit, the
payment it creates can be spent by Bob with a segwit transaction.
Pay-to-Witness-Script-Hash inside Pay-to-Script-Hash
Similarly, a P2WSH witness program for a multisig script or other
complicated script
can be embedded inside a P2SH script and address, making it possible for
any wallet
to make payments that are segwit compatible.
As we saw in “Pay-to-Witness-Script-Hash (P2WSH)” on page 333, Mohammed’s
company is using Segregated Witness payments to multisignature scripts. To
make it
possible for any client to pay his company, regardless of whether their
wallets are
upgraded for segwit, Mohammed’s wallet can embed the P2WSH witness program
inside a P2SH script.
First, Mohammed’s wallet creates the P2WSH witness program that
corresponds to
the multisignature script, hashed with SHA256:
0 9592d601848d04b172905e0ddb0adde59f1590f1e553ffc81ddc4b0ed927dd73
Then, the witness program itself is hashed with SHA256 and RIPEMD160,
producing
a new 20-byte hash, as used in traditional P2SH:
86762607e8fe87c0c37740cddee880988b9455b2
Next, Mohammed’s wallet puts the hash into a P2SH script:
HASH160 86762607e8fe87c0c37740cddee880988b9455b2 EQUAL
Finally, the wallet constructs a bitcoin address from this script:
3Dwz1MXhM6EfFoJChHCxh1jWHb8GQqRenG
Now, Mohammed’s clients can make payments to this address without any need
to
support segwit. Mohammed’s company can then construct segwit transactions
to
spend these payments, taking advantage of segwit features including lower
transac‐
tion fees.
Segregated Witness
|
337
Segregated Witness addresses
After segwit is deployed on the bitcoin network, it will take some time
until wallets
are upgraded. It is quite likely therefore that segwit will mostly be used
embedded in
P2SH, as we saw in the previous section, at least for several months.
Eventually, however, almost all wallets will be able to support segwit
payments. At
that time it will no longer be necessary to embed segwit in P2SH. It is
therefore likely
that a new form of bitcoin address will be created, one that indicates the
recipient is
segwit-aware and that directly encodes a witness program. There have been
a number
of proposals for a Segregated Witness address scheme, but none have been
actively
pursued.
Transaction identifiers
One of the greatest benefits of Segregated Witness is that it eliminates
third-party
transaction malleability.
Before segwit, transactions could have their signatures subtly modified by
third par‐
ties, changing their transaction ID (hash) without changing any
fundamental proper‐
ties (inputs, outputs, amounts). This created opportunities for
denial-of-service
attacks as well as attacks against poorly written wallet software that
assumed uncon‐
firmed transaction hashes were immutable.
With the introduction of Segregated Witness, transactions have two
identifiers, txid
and wtxid. The traditional transaction ID txid is the double-SHA256 hash
of the
serialized transaction, without the witness data. A transaction wtxid is
the double-
SHA256 hash of the new serialization format of the transaction with
witness data.
The traditional txid is calculated in exactly the same way as with a
nonsegwit trans‐
action. However, since the segwit transaction has empty scriptSigs in
every input,
there is no part of the transaction that can be modified by a third party.
Therefore, in
a segwit transaction, the txid is immutable by a third party, even when
the transac‐
tion is unconfirmed.
The wtxid is like an “extended” ID, in that the hash also incorporates the
witness
data. If a transaction is transmitted without witness data, then the wtxid
and txid are
identical. Note than since the wtxid includes witness data (signatures)
and since wit‐
ness data may be malleable, the wtxid should be considered malleable until
the trans‐
action is confirmed. Only the txid of a segwit transaction can be
considered
immutable by third parties and only if all the inputs of the transaction
are segwit
inputs.
338
|
Appendix D: Segregated Witness
Segregated Witness transactions have two IDs: txid and wtxid.
The txid is the hash of the transaction without the witness data
and the wtxid is the hash inclusive of witness data. The txid of a
transaction where all inputs are segwit inputs is not susceptible to
third-party transaction malleability.
Segregated Witness’ New Signing Algorithm
Segregated Witness modifies the semantics of the four signature
verification func‐
tions (CHECKSIG, CHECKSIGVERIFY, CHECKMULTISIG, and CHECKMULTISIGVERIFY),
changing the way a transaction commitment hash is calculated.
Signatures in bitcoin transactions are applied on a commitment hash, which
is calcu‐
lated from the transaction data, locking specific parts of the data
indicating the sign‐
er’s commitment to those values. For example, in a simple SIGHASH_ALL type
signature, the commitment hash includes all inputs and outputs.
Unfortunately, the way the commitment hash was calculated introduced the
possibil‐
ity that a node verifying the signature can be forced to perform a
significant number
of hash computations. Specifically, the hash operations increase in O(n 2)
with respect
to the number of signature operations in the transaction. An attacker
could therefore
create a transaction with a very large number of signature operations,
causing the
entire bitcoin network to have to perform hundreds or thousands of hash
operations
to verify the transaction.
Segwit represented an opportunity to address this problem by changing the
way the
commitment hash is calculated. For segwit version 0 witness programs,
signature ver‐
ification occurs using an improved commitment hash algorithm as specified
in
BIP-143.
The new algorithm achieves two important goals. Firstly, the number of
hash opera‐
tions increases by a much more gradual O(n) to the number of signature
operations,
reducing the opportunity to create denial-of-service attacks with overly
complex
transactions. Secondly, the commitment hash now also includes the value
(amounts)
of each input as part of the commitment. This means that a signer can
commit to a
specific input value without needing to “fetch” and check the previous
transaction
referenced by the input. In the case of offline devices, such as hardware
wallets, this
greatly simplifies the communication between the host and the hardware
wallet,
removing the need to stream previous transactions for validation. A
hardware wallet
can accept the input value “as stated” by an untrusted host. Since the
signature is
invalid if that input value is not correct, the hardware wallet doesn’t
need to validate
the value before signing the input.
Segregated Witness
|
339
Economic Incentives for Segregated Witness
Bitcoin mining nodes and full nodes incur costs for the resources used to
support the
bitcoin network and the blockchain. As the volume of bitcoin transactions
increases,
so does the cost of resources (CPU, network bandwidth, disk space,
memory). Miners
are compensated for these costs through fees that are proportional to the
size (in
bytes) of each transaction. Nonmining full nodes are not compensated, so
they incur
these costs because they have a need to run an authoritative fully
validating full-index
node, perhaps because they use the node to operate a bitcoin business.
Without transaction fees, the growth in bitcoin data would arguably
increase dramat‐
ically. Fees are intended to align the needs of bitcoin users with the
burden their
transactions impose on the network, through a market-based price discovery
mecha‐
nism.
The calculation of fees based on transaction size treats all the data in
the transaction
as equal in cost. But from the perspective of full nodes and miners, some
parts of a
transaction carry much higher costs. Every transaction added to the
bitcoin network
affects the consumption of four resources on nodes:
Disk Space
Every transaction is stored in the blockchain, adding to the total size of
the
blockchain. The blockchain is stored on disk, but the storage can be
optimized by
“pruning” older transactions.
CPU
Every transaction must be validated, which requires CPU time.
Bandwidth
Every transaction is transmitted (through flood propagation) across the
network
at least once. Without any optimization in the block propagation protocol,
trans‐
actions are transmitted again as part of a block, doubling the impact on
network
capacity.
Memory
Nodes that validate transactions keep the UTXO index or the entire UTXO
set in
memory to speed up validation. Because memory is at least one order of
magni‐
tude more expensive than disk, growth of the UTXO set contributes
dispropor‐
tionately to the cost of running a node.
As you can see from the list, not every part of a transaction has an equal
impact on
the cost of running a node or on the ability of bitcoin to scale to
support more trans‐
actions. The most expensive part of a transaction are the newly created
outputs, as
they are added to the in-memory UTXO set. By comparison, signatures (aka
witness
data) add the least burden to the network and the cost of running a node,
because
witness data are only validated once and then never used again.
Furthermore, imme‐
340
|
Appendix D: Segregated Witness
diately after receiving a new transaction and validating witness data,
nodes can dis‐
card that witness data. If fees are calculated on transaction size,
without
discriminating between these two types of data, then the market incentives
of fees are
not aligned with the actual costs imposed by a transaction. In fact, the
current fee
structure actually encourages the opposite behavior, because witness data
is the larg‐
est part of a transaction.
The incentives created by fees matter because they affect the behavior of
wallets. All
wallets must implement some strategy for assembling transactions that
takes into
consideration a number of factors, such as privacy (reducing address
reuse), frag‐
mentation (making lots of loose change), and fees. If the fees are
overwhelmingly
motivating wallets to use as few inputs as possible in transactions, this
can lead to
UTXO picking and change address strategies that inadvertently bloat the
UTXO set.
Transactions consume UTXO in their inputs and create new UTXO with their
out‐
puts. A transaction, therefore, that has more inputs than outputs will
result in a
decrease in the UTXO set, whereas a transaction that has more outputs than
inputs
will result in an increase in the UTXO set. Let’s consider the difference
between inputs
and outputs and call that the “Net-new-UTXO.” That’s an important metric,
as it tells
us what impact a transaction will have on the most expensive network-wide
resource,
the in-memory UTXO set. A transaction with positive Net-new-UTXO adds to
that
burden. A transaction with a negative Net-new-UTXO reduces the burden. We
would
therefore want to encourage transactions that are either negative
Net-new-UTXO or
neutral with zero Net-new-UTXO.
Let’s look at an example of what incentives are created by the transaction
fee calcula‐
tion, with and without Segregated Witness. We will look at two different
transactions.
Transaction A is a 3-input, 2-output transaction, which has a Net-new-UTXO
metric
of –1, meaning it consumes one more UTXO than it creates, reducing the
UTXO set
by one. Transaction B is a 2-input, 3-output transaction, which has a
Net-new-UTXO
metric of 1, meaning it adds one UTXO to the UTXO set, imposing additional
cost
on the entire bitcoin network. Both transactions use multisignature
(2-of-3) scripts to
demonstrate how complex scripts increase the impact of segregated witness
on fees.
Let’s assume a transaction fee of 30 satoshi per byte and a 75% fee
discount on witness
data:
Without Segregated Witness
Transaction A fee: 25,710 satoshi
Transaction B fee: 18,990 satoshi
With Segregated Witness
Transaction A fee: 8,130 satoshi
Transaction B fee: 12,045 satoshi
Segregated Witness
|
341
Both transactions are less expensive when segregated witness is
implemented. But
comparing the costs between the two transactions, we see that before
Segregated Wit‐
ness, the fee is higher for the transaction that has a negative
Net-new-UTXO. After
Segregated Witness, the transaction fees align with the incentive to
minimize new
UTXO creation by not inadvertently penalizing transactions with many
inputs.
Segregated Witness therefore has two main effects on the fees paid by
bitcoin users.
Firstly, segwit reduces the overall cost of transactions by discounting
witness data and
increasing the capacity of the bitcoin blockchain. Secondly, segwit’s
discount on wit‐
ness data corrects a misalignment of incentives that may have
inadvertently created
more bloat in the UTXO set.
342
|
Appendix D: Segregated Witness
APPENDIX E
Bitcore
Bitcore is a suite of tools provided by BitPay. Its goal is to provide
easy-to-use tools
for Bitcoin developers. Almost all of Bitcore’s code is written in
JavaScript. There are
some modules written specifically for NodeJS. Finally, the “node” module
of Bitcore
includes Bitcoin Core’s C++ code. Please see https://bitcore.io for more
information.
Bitcore’s Feature List
• Bitcoin full node (bitcore-node)
• Block explorer (insight)
• Block, transaction, and wallet utilities (bitcore-lib)
• Communicating directly with Bitcoin’s P2P network (bitcore-p2p)
• Seed entropy mnemonic generation (bitcore-mnemonic)
• Payment protocol (bitcore-payment-protocol)
• Message verification and signing (bitcore-message)
• Elliptic curve Integrated Encryption Scheme (bitcore-ecies)
• Wallet service (bitcore-wallet-service)
• Wallet client (bitcore-wallet-client)
• Playground (bitcore-playground)
• Integrating services directly with Bitcoin Core (bitcore-node)
343
Bitcore Library Examples
Prerequisities
• NodeJS >= 4.x or use our hosted online playground
If using NodeJS and the node REPL:
$ npm install -g bitcore-lib bitcore-p2p
$ NODE_PATH=$(npm list -g | head -1)/node_modules node
Wallet Examples using bitcore-lib
Creating a new bitcoin address with associated private key:
> bitcore = require('bitcore-lib')
> privateKey = new bitcore.PrivateKey()
> address = privateKey.toAddress().toString()
Creating a hierarchical deterministic private key and address:
> hdPrivateKey = bitcore.HDPrivateKey()
> hdPublicKey = bitcore.HDPublicKey(hdPrivateKey)
> hdAddress = new bitcore.Address(hdPublicKey.publicKey).toString()
Creating and signing a transaction from a UTXO:
> utxo = {
txId: transaction id containing an unspent output,
outputIndex: output indexi e.g. 0,
address: addressOfUtxo,
script: bitcore.Script.buildPublicKeyHashOut(addressOfUtxo).toString(),
satoshis: amount sent to the address
}
> fee = 3000 //set appropriately for conditions on the network
> tx = new bitcore.Transaction()
.from(utxo)
.to(address, 35000)
.fee(fee)
.enableRBF()
.sign(privateKeyOfUtxo)
Replace the last transaction in the mempool (replace-by-fee):
> rbfTx = new Transaction()
.from(utxo)
.to(address, 35000)
.fee(fee*2)
.enableRBF()
.sign(privateKeyOfUtxo);
> tx.serialize();
> rbfTx.serialize();
344
|
Appendix E: Bitcore
Broadcasting a transaction to the Bitcoin network (note: broadcast valid
transactions
only; refer to https://bitnodes.21.co/nodes for peer hosts):
1. Copy the code below into a file called broadcast.js.
2. The tx and rbfTx variables are the output of tx.serialize() and
rbfTx.serial
ize(), respectively.
3. In order to replace-by-fee, the peer must support bitcoind option
mempoolre
place and have it set to 1.
4. Run the file node broadcast.js:
var p2p = require('bitcore-p2p');
var bitcore = require('bitcore-lib');
var tx = new bitcore.Transaction('output from serialize function');
var rbfTx = new bitcore.Transaction('output from serialize function');
var host = 'ip address'; //use valid peer listening on tcp 8333
var peer = new p2p.Peer({host: host});
var messages = new p2p.Messages();
peer.on('ready', function() {
var txs = [messages.Transaction(tx), messages.Transaction(rbfTx)];
var index = 0;
var interval = setInterval(function() {
peer.sendMessage(txs[index++]);
console.log('tx: ' + index + ' sent');
if (index === txs.length) {
clearInterval(interval);
console.log('disconnecting from peer: ' + host);
peer.disconnect();
}
}, 2000);
});
peer.connect();
Bitcore
|
345
APPENDIX F
pycoin, ku, and tx
The Python library pycoin, originally written and maintained by Richard
Kiss, is a
Python-based library that supports manipulation of bitcoin keys and
transactions,
even supporting the scripting language enough to properly deal with
nonstandard
transactions.
The pycoin library supports both Python 2 (2.7.x) and Python 3 (after 3.3)
and comes
with some handy command-line utilities, ku and tx.
Key Utility (KU)
The command-line utility ku (“key utility”) is a Swiss Army knife for
manipulating
keys. It supports BIP-32 keys, WIF, and addresses (bitcoin and alt coins).
Following
are some examples.
Create a BIP-32 key using the default entropy sources of GPG and
/dev/random:
$ ku create
input
: create
network
: Bitcoin
wallet key
: xprv9s21ZrQH143K3LU5ctPZTBnb9kTjA5Su9DcWHvXJe-
miJBsY7VqXUG7hipgdWaU
m2nhnzdvxJf5KJo9vjP2nABX65c5sFsWsV8oXcbpehtJi
public version : xpub661MyMwAqRbcFpYYiuvZpKjKhnJD-
ZYAkWSY76JvvD7FH4fsG3Nqiov2CfxzxY8
DGcpfT56AMFeo8M8KPkFMfLUtvwjwb6WPv8rY65L2q8Hz
tree depth
: 0
fingerprint
: 9d9c6092
parent f'print : 00000000
child index
: 0
chain code
:
80574fb260edaa4905bc86c9a47d30c697c50047ed466c0d4a5167f6821e8f3c
347
private key
: yes
secret exponent :
112471538590155650688604752840386134637231974546906847202389294096567806844862
hex
:
f8a8a28b28a916e1043cc0aca52033a18a13cab1638d544006469bc171fddfbe
wif
: L5Z54xi6qJusQT42JHA44mfPVZGjyb4XBRWfxAzUWwRiGx1kV4sP
uncompressed
: 5KhoEavGNNH4GHKoy2Ptu4KfdNp4r56L5B5un8FP6RZnbsz5Nmb
public pair x
:
76460638240546478364843397478278468101877117767873462127021560368290114016034
public pair y
:
59807879657469774102040120298272207730921291736633247737077406753676825777701
x as hex
:
a90b3008792432060fa04365941e09a8e4adf928bdbdb9dad41131274e379322
y as hex
:
843a0f6ed9c0eb1962c74533795406914fe3f1957c5238951f4fe245a4fcd625
y parity
: odd
key pair as sec :
03a90b3008792432060fa04365941e09a8e4adf928bdbdb9dad41131274e379322
uncompressed
:
04a90b3008792432060fa04365941e09a8e4adf928bdbdb9dad41131274e379322
843a0f6ed9c0eb1962c74533795406914fe3f1957c5238951f4fe245a4fcd625
hash160
: 9d9c609247174ae323acfc96c852753fe3c8819d
uncompressed
: 8870d869800c9b91ce1eb460f4c60540f87c15d7
Bitcoin address : 1FNNRQ5fSv1wBi5gyfVBs2rkNheMGt86sp
uncompressed
: 1DSS5isnH4FsVaLVjeVXewVSpfqktdiQAM
Create a BIP-32 key from a passphrase:
The passphrase in this example is way too easy to guess.
$ ku P:foo
input
: P:foo
network
: Bitcoin
wallet key
:
xprv9s21ZrQH143K31AgNK5pyVvW23gHnkBq2wh5aEk6g1s496M8ZMjxncCKZKgb5j
ZoY5eSJMJ2Vbyvi2hbmQnCuHBujZ2WXGTux1X2k9Krdtq
public version :
xpub661MyMwAqRbcFVF9ULcqLdsEa5WnCCugQAcgNd9iEMQ31tgH6u4DLQWo-
QayvtS
VYFvXz2vPPpbXE1qpjoUFidhjFj82pVShWu9curWmb2zy
tree depth
: 0
fingerprint
: 5d353a2e
parent f'print : 00000000
child index
: 0
chain code
:
5eeb1023fd6dd1ae52a005ce0e73420821e1d90e08be980a85e9111fd7646bbc
private key
: yes
348
|
Appendix F: pycoin, ku, and tx
secret exponent :
65825730547097305716057160437970790220123864299761908948746835886007793998275
hex
:
91880b0e3017ba586b735fe7d04f1790f3c46b818a2151fb2def5f14dd2fd9c3
wif
: L26c3H6jEPVSqAr1usXUp9qtQJw6NHgApq6Ls4ncyqtsvcq2MwKH
uncompressed
: 5JvNzA5vXDoKYJdw8SwwLHxUxaWvn9mDea6k1vRPCX7KLUVWa7W
public pair x
:
81821982719381104061777349269130419024493616650993589394553404347774393168191
public pair y
:
58994218069605424278320703250689780154785099509277691723126325051200459038290
x as hex
:
b4e599dfa44555a4ed38bcfff0071d5af676a86abf123c5b4b4e8e67a0b0b13f
y as hex
:
826d8b4d3010aea16ff4c1c1d3ae68541d9a04df54a2c48cc241c2983544de52
y parity
: even
key pair as sec :
02b4e599dfa44555a4ed38bcfff0071d5af676a86abf123c5b4b4e8e67a0b0b13f
uncompressed
:
04b4e599dfa44555a4ed38bcfff0071d5af676a86abf123c5b4b4e8e67a0b0b13f
826d8b4d3010aea16ff4c1c1d3ae68541d9a04df54a2c48cc241c2983544de52
hash160
: 5d353a2ecdb262477172852d57a3f11de0c19286
uncompressed
: e5bd3a7e6cb62b4c820e51200fb1c148d79e67da
Bitcoin address : 19Vqc8uLTfUonmxUEZac7fz1M5c5ZZbAii
uncompressed
: 1MwkRkogzBRMehBntgcq2aJhXCXStJTXHT
Get info as JSON:
$ ku P:foo -P -j
{
"y_parity": "even",
"public_pair_y_hex":
"826d8b4d3010aea16ff4c1c1d3ae68541d9a04df54a2c48cc241c2983544de52",
"private_key": "no",
"parent_fingerprint": "00000000",
"tree_depth": "0",
"network": "Bitcoin",
"btc_address_uncompressed": "1MwkRkogzBRMehBntgcq2aJhXCXStJTXHT",
"key_pair_as_sec_uncompressed":
"04b4e599dfa44555a4ed38bcfff0071d5af676a86abf123c5b4b4e8e67a0b0b13f826d8b4d3010a
ea16ff4c1c1d3ae68541d9a04df54a2c48cc241c2983544de52",
"public_pair_x_hex":
"b4e599dfa44555a4ed38bcfff0071d5af676a86abf123c5b4b4e8e67a0b0b13f",
"wallet_key":
"xpub661MyMwAqRbcFVF9ULcqLdsEa5WnCCugQAcgNd9iEMQ31tgH6u4DLQWo
QayvtSVYFvXz2vPPpbXE1qpjoUFidhjFj82pVShWu9curWmb2zy",
"chain_code":
"5eeb1023fd6dd1ae52a005ce0e73420821e1d90e08be980a85e9111fd7646bbc",
"child_index": "0",
"hash160_uncompressed": "e5bd3a7e6cb62b4c820e51200fb1c148d79e67da",
"btc_address": "19Vqc8uLTfUonmxUEZac7fz1M5c5ZZbAii",
"fingerprint": "5d353a2e",
"hash160": "5d353a2ecdb262477172852d57a3f11de0c19286",
pycoin, ku, and tx
|
349
"input": "P:foo",
"public_pair_x":
"81821982719381104061777349269130419024493616650993589394553404347774393168191",
"public_pair_y":
"58994218069605424278320703250689780154785099509277691723126325051200459038290",
"key_pair_as_sec":
"02b4e599dfa44555a4ed38bcfff0071d5af676a86abf123c5b4b4e8e67a0b0b13f"
}
Public BIP32 key:
$ ku -w -P P:foo
xpub661MyMwAqRbcFVF9ULcqLdsEa5WnCCugQAcgNd9iEMQ31tgH6u4DLQWoQayvtS-
VYFvXz2vPPpbXE1qpjoUFidhjFj82pVShWu9curWmb2zy
Generate a subkey:
$ ku -w -s3/2 P:foo
xprv9wTErTSkjVyJa1v4cUTFMFkWMe5eu8ErbQcs9xajn-
sUzCBT7ykHAwdrxvG3g3f6BFk7ms5hHBvmbdutNmyg6iogWKxx6mefEw4M8EroLgKj
Hardened subkey:
$ ku -w -s3/2H P:foo
xprv9wTErTSu5AWGk-
DeUPmqBcbZWX1xq85ZNX9iQRQW9DXwygFp7iRGJo79dsVctcsCHsnZ3XU3DhsuaGZbDh8iDkBN45k67U
KsJUXM1JfRCdn1
WIF:
$ ku -W P:foo
L26c3H6jEPVSqAr1usXUp9qtQJw6NHgApq6Ls4ncyqtsvcq2MwKH
Address:
$ ku -a P:foo
19Vqc8uLTfUonmxUEZac7fz1M5c5ZZbAii
Generate a bunch of subkeys:
$ ku P:foo -s 0/0-5 -w
xprv9xWkBDfyBXmZjBG9EiXBpy67KK72fphUp9utJokEBFtjsjiuKUUDF5V3TU8U8cDzytqYn-
Sekc8bYuJS8G3bhXxKWB89Ggn2dzLcoJsuEdRK
xprv9xWkBDfyBXmZnzKf3bAGifK593gT7WJZPnYAmvc77gUQ-
Vej5QHckc5Adtwxa28ACmANi9XhCrRvtFqQcUxt8rUgFz3souMiDdWxJDZnQxzx
xprv9xWkBDfyBXmZqdXA8y4SWqfBdy71gSW9sjx9JpCiJEiBwSMQyRxan6srXUPBtj3PTxQFkZJAi-
woUpmvtrxKZu4zfsnr3pqyy2vthpkwuoVq
xprv9xWkBDfyBXmZsA85GyWj9uYPyoQv826YAadKWMaaEosNrFBKgj2TqWuiWY3zuq-
xYGpHfv9cnGj5P7e8EskpzKL1Y8Gk9aX6QbryA5raK73p
xprv9xWkBDfyBXmZv2q3N66hhZ8DAcEnQDnXML1J62krJAcf7Xb1HJwuW2VMJQrCofY2jtFXdiEY8UsR
NJfqK6DAdyZXoMvtaLHyWQx3FS4A9zw
xprv9xWkBDfyBXmZw4jEYXU-
HYc9fT25k9irP87n2RqfJ5bqbjKdT84Mm7Wtc2xmzFuKg7iYf7XFHKkSsaYKWKJbR54bnyAD9GzjUY-
bAYTtN4ruo
350
|
Appendix F: pycoin, ku, and tx
Generate the corresponding addresses:
$ ku P:foo -s 0/0-5 -a
1MrjE78H1R1rqdFrmkjdHnPUdLCJALbv3x
1AnYyVEcuqeoVzH96zj1eYKwoWfwte2pxu
1GXr1kZfxE1FcK6ZRD5sqqqs5YfvuzA1Lb
116AXZc4bDVQrqmcinzu4aaPdrYqvuiBEK
1Cz2rTLjRM6pMnxPNrRKp9ZSvRtj5dDUML
1WstdwPnU6HEUPme1DQayN9nm6j7nDVEM
Generate the corresponding WIFs:
$ ku P:foo -s 0/0-5 -W
L5a4iE5k9gcJKGqX3FWmxzBYQc29PvZ6pgBaePLVqT5YByEnBomx
Kyjgne6GZwPGB6G6kJEhoPbmyjMP7D5d3zRbHVjwcq4iQXD9QqKQ
L4B3ygQxK6zH2NQGxLDee2H9v4Lvwg14cLJW7QwWPzCtKHdWMaQz
L2L2PZdorybUqkPjrmhem4Ax5EJvP7ijmxbNoQKnmTDMrqemY8UF
L2oD6vA4TUyqPF8QG4vhUFSgwCyuuvFZ3v8SKHYFDwkbM765Nrfd
KzChTbc3kZFxUSJ3Kt54cxsogeFAD9CCM4zGB22si8nfKcThQn8C
Check that it works by choosing a BIP32 string (the one corresponding to
subkey
0/3):
$ ku -W
xprv9xWkBDfyBXmZsA85GyWj9uYPyoQv826YAadKWMaaEosNrFBKgj2TqWuiWY3zuq-
xYGpHfv9cnGj5P7e8EskpzKL1Y8Gk9aX6QbryA5raK73p
L2L2PZdorybUqkPjrmhem4Ax5EJvP7ijmxbNoQKnmTDMrqemY8UF
$ ku -a
xprv9xWkBDfyBXmZsA85GyWj9uYPyoQv826YAadKWMaaEosNrFBKgj2TqWuiWY3zuq-
xYGpHfv9cnGj5P7e8EskpzKL1Y8Gk9aX6QbryA5raK73p
116AXZc4bDVQrqmcinzu4aaPdrYqvuiBEK
Yep, looks familiar.
From secret exponent:
$ ku 1 наput
: 1
network
: Bitcoin
secret exponent : 1
hex
: 1
wif
: KwDiBf89QgGbjEhKnhXJuH7LrciVrZi3qYjgd9M7rFU73sVHnoWn
uncompressed
: 5HpHagT65TZzG1PH3CSu63k8DbpvD8s5ip4nEB3kEsreAnchuDf
public pair x
:
55066263022277343669578718895168534326250603453777594175500187360389116729240
public pair y
:
32670510020758816978083085130507043184471273380659243275938904335757337482424
x as hex
:
79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
y as hex
:
483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
y parity
: even
key pair as sec :
0279be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
uncompressed
:
pycoin, ku, and tx
|
351
0479be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
hash160
: 751e76e8199196d454941c45d1b3a323f1433bd6
uncompressed
: 91b24bf9f5288532960ac687abb035127b1d28a5
Bitcoin address : 1BgGZ9tcN4rm9KBzDn7KprQz87SZ26SAMH
uncompressed
: 1EHNa6Q4Jz2uvNExL497mE43ikXhwF6kZm
Litecoin version:
$ ku -nL 1 наput
: 1
network
: Litecoin
secret exponent : 1
hex
: 1
wif
: T33ydQRKp4FCW5LCLLUB7deioUMoveiwekdwUwyfRDeGZm76aUjV
uncompressed
: 6u823ozcyt2rjPH8Z2ErsSXJB5PPQwK7VVTwwN4mxLBFrao69XQ
public pair x
:
55066263022277343669578718895168534326250603453777594175500187360389116729240
public pair y
:
32670510020758816978083085130507043184471273380659243275938904335757337482424
x as hex
:
79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
y as hex
:
483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
y parity
: even
key pair as sec :
0279be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
uncompressed
:
0479be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
hash160
: 751e76e8199196d454941c45d1b3a323f1433bd6
uncompressed
: 91b24bf9f5288532960ac687abb035127b1d28a5
Litecoin address : LVuDpNCSSj6pQ7t9Pv6d6sUkLKoqDEVUnJ
uncompressed
: LYWKqJhtPeGyBAw7WC8R3F7ovxtzAiubdM
Dogecoin WIF:
$ ku -nD -W 1
QNcdLVw8fHkixm6NNyN6nVwxKek4u7qrioRbQmjxac5TVoTtZuot
From public pair (on Testnet):
$ ku -nT
55066263022277343669578718895168534326250603453777594175500187360389116729240,ev
en
input
:
550662630222773436695787188951685343262506034537775941755001873603
89116729240,even
network
: Bitcoin testnet
public pair x
:
352
| Appendix F: pycoin, ku, and tx
55066263022277343669578718895168534326250603453777594175500187360389116729240
public pair y
:
32670510020758816978083085130507043184471273380659243275938904335757337482424
x as hex
:
79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
y as hex
:
483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
y parity
: even
key pair as sec
:
0279be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
uncompressed
:
0479be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
hash160
: 751e76e8199196d454941c45d1b3a323f1433bd6
uncompressed
: 91b24bf9f5288532960ac687abb035127b1d28a5
Bitcoin testnet address : mrCDrCybB6J1vRfbwM5hemdJz73FwDBC8r
uncompressed
: mtoKs9V381UAhUia3d7Vb9GNak8Qvmcsme
From hash160:
$ ku 751e76e8199196d454941c45d1b3a323f1433bd6
input
:
751e76e8199196d454941c45d1b3a323f1433bd6
network
:
Bitcoin
hash160
:
751e76e8199196d454941c45d1b3a323f1433bd6
Bitcoin address
:
1BgGZ9tcN4rm9KBzDn7KprQz87SZ26SAMH
As a Dogecoin address:
$ ku -nD 751e76e8199196d454941c45d1b3a323f1433bd6
input
:
751e76e8199196d454941c45d1b3a323f1433bd6
network
:
Dogecoin
hash160
:
751e76e8199196d454941c45d1b3a323f1433bd6
Dogecoin address
:
DFpN6QqFfUm3gKNaxN6tNcab1FArL9cZLE
Transaction Utility (TX)
The command-line utility tx will display transactions in human-readable
form, fetch
base transactions from pycoin’s transaction cache or from web services
(block‐
chain.info, blockcypher.com, blockr.io and chain.so are currently
supported), merge
transactions, add or delete inputs or outputs, and sign transactions.
Following are some examples.
View the famous “pizza” transaction:
$ tx 49d2adb6e476fa46d8357babf78b1b501fd39e177ac7833124b3f67b17c40c2a
warning: consider setting environment variable
PYCOIN_CACHE_DIR=~/.pycoin_cache
to cache transactions fetched via web services
warning: no service providers found for get_tx; consider setting
environment
variable PYCOIN_BTC_PROVIDERS
pycoin, ku, and tx
|
353
usage: tx [-h] [-t TRANSACTION_VERSION] [-l LOCK_TIME] [-n NETWORK] [-a]
[-i address] [-f path-to-private-keys] [-g GPG_ARGUMENT]
[--remove-tx-in tx_in_index_to_delete]
[--remove-tx-out tx_out_index_to_delete] [-F transaction-fee] [-u]
[-b BITCOIND_URL] [-o path-to-output-file]
argument [argument ...]
tx: error: can't find Tx with id
49d2adb6e476fa46d8357babf78b1b501fd39e177ac7833124b3f67b17c40c2a
Oops! We don’t have web services set up. Let’s do that now:
$ PYCOIN_CACHE_DIR=~/.pycoin_cache
$ PYCOIN_BTC_PROVIDERS="block.io blockchain.info blockexplorer.com"
$ export PYCOIN_CACHE_DIR PYCOIN_BTC_PROVIDERS
It’s not done automatically so a command-line tool won’t leak potentially
private
information about what transactions you’re interested in to a third-party
website. If
you don’t care, you could put these lines into your .profile.
Let’s try again:
$ tx 49d2adb6e476fa46d8357babf78b1b501fd39e177ac7833124b3f67b17c40c2a
Version: 1 tx hash
49d2adb6e476fa46d8357babf78b1b501fd39e177ac7833124b3f67b17c40c2a 159 bytes
TxIn count: 1; TxOut count: 1
Lock time: 0 (valid anytime)
Input:
0:
(unknown) from
1e133f7de73ac7d074e2746a3d6717dfc99ecaa8e9f9fade2cb8b0b20a5e0441:0
Output:
0: 1CZDM6oTttND6WPdt3D6bydo7DYKzd9Qik receives 10000000.00000 mBTC
Total output 10000000.00000 mBTC
including unspents in hex dump since transaction not fully signed
010000000141045e0ab2b0b82cde-
faf9e9a8ca9ec9df17673d6a74e274d0c73ae77d3f131e000000004a493046022100a7f26eda8749
31999c90f87f01ff1ffc76bcd058fe16137e0e63fdb6a35c2d78022100a61e9199238eb73f07c8f2
09504c84b80f03e30ed8169edd44f80ed17ddf451901ffffffff010010a5d4e80000001976a9147e
c1003336542cae8bded8909cdd6b5e48ba0ab688ac00000000
** can't validate transaction as source transactions missing
The final line appears because to validate the transactions’ signatures,
you technically
need the source transactions. So let’s add -a to augment the transactions
with source
information:
$ tx -a 49d2adb6e476fa46d8357babf78b1b501fd39e177ac7833124b3f67b17c40c2a
warning: transaction fees recommendations casually calculated and
estimates may
be incorrect
warning: transaction fee lower than (casually calculated) expected value
of 0.1
mBTC, transaction might not propogate
Version: 1 tx hash
49d2adb6e476fa46d8357babf78b1b501fd39e177ac7833124b3f67b17c40c2a 159 bytes
TxIn count: 1; TxOut count: 1
354
|
Appendix F: pycoin, ku, and tx
Lock time: 0 (valid anytime)
Input:
0: 17WFx2GQZUmh6Up2NDNCEDk3deYomdNCfk from
1e133f7de73ac7d074e2746a3d6717dfc99ecaa8e9f9fade2cb8b0b20a5e0441:0
10000000.00000 mBTC sig ok
Output:
0: 1CZDM6oTttND6WPdt3D6bydo7DYKzd9Qik receives 10000000.00000 mBTC
Total input 10000000.00000 mBTC
Total output 10000000.00000 mBTC
Total fees
0.00000 mBTC
010000000141045e0ab2b0b82cde-
faf9e9a8ca9ec9df17673d6a74e274d0c73ae77d3f131e000000004a493046022100a7f26eda8749
31999c90f87f01ff1ffc76bcd058fe16137e0e63fdb6a35c2d78022100a61e9199238eb73f07c8f2
09504c84b80f03e30ed8169edd44f80ed17ddf451901ffffffff010010a5d4e80000001976a9147e
c1003336542cae8bded8909cdd6b5e48ba0ab688ac00000000
all incoming transaction values validated
Now, let’s look at unspent outputs for a specific address (UTXO). In block
#1, we see a
coinbase transaction to 12c6DSiU4Rq3P4ZxziKxzrL5LmMBrzjrJX. Let’s use
fetch_unspent to find all coins in this address:
$ fetch_unspent 12c6DSiU4Rq3P4ZxziKxzrL5LmMBrzjrJX
a3a6f902a51a2cbebede144e48a88c05e608c2cce28024041a5b9874013a1e2a/
0/76a914119b098e2e980a229e139a9ed01a469e518e6f2688ac/333000
cea36d008badf5c7866894b191d3239de9582d89b6b452b596f1f1b76347f8cb/
31/76a914119b098e2e980a229e139a9ed01a469e518e6f2688ac/10000
065ef6b1463f552f675622a5d1fd2c08d6324b4402049f68e767a719e2049e8d/
86/76a914119b098e2e980a229e139a9ed01a469e518e6f2688ac/10000
a66dddd42f9f2491d3c336ce5527d45cc5c2163aaed3158f81dc054447f447a2/0/76a914119b098
e2e980a229e139a9ed01a469e518e6f2688ac/10000
ffd901679de65d4398de90cefe68d2c3ef073c41f7e8dbec2fb5cd75fe71dfe7/0/76a914119b098
e2e980a229e139a9ed01a469e518e6f2688ac/100
d658ab87cc053b8dbcfd4aa2717fd23cc3edfe90ec75351fadd6a0f7993b461d/
5/76a914119b098e2e980a229e139a9ed01a469e518e6f2688ac/911
36ebe0ca3237002acb12e1474a3859bde0ac84b419ec4ae373e63363ebef731c/
1/76a914119b098e2e980a229e139a9ed01a469e518e6f2688ac/100000
fd87f9adebb17f4ebb1673da76ff48ad29e64b7afa02fda0f2c14e43d220fe24/0/76a914119b098
e2e980a229e139a9ed01a469e518e6f2688ac/1
dfdf0b375a987f17056e5e919ee6eadd87dad36c09c4016d4a03cea15e5c05e3/1/76a914119b098
e2e980a229e139a9ed01a469e518e6f2688ac/1337
cb2679bfd0a557b2dc0d8a6116822f3fcbe281ca3f3e18d3855aa7ea378fa373/0/76a914119b098
e2e980a229e139a9ed01a469e518e6f2688ac/1337
d6be34ccf6edddc3cf69842dce99fe503bf632ba2c2adb0f95c63f6706ae0c52/1/76a914119b098
e2e980a229e139a9ed01a469e518e6f2688ac/2000000
0e3e2357e806b6cdb1f70b54c3a3a17b6714ee1f0e68bebb44a74b1efd512098/0/410496b538e85
3519c726a2c91e61ec11600ae1390813a627c66fb8be7947be63c52da7589379515d4e0a604f8141
781e62294721166bf621e73a82cbf2342c858eeac/5000000000
pycoin, ku, and tx
|
355
APPENDIX G
Bitcoin Explorer (bx) Commands
Bitcoin Explorer (bx) is a command-line tool that offers a variety of
commands for
key management and transaction construction. It is part of the libbitcoin
bitcoin
library.
Usage: bx COMMAND [--help]
Info: The bx commands are:
address-decode
address-embed
address-encode
address-validate
base16-decode
base16-encode
base58-decode
base58-encode
base58check-decode
base58check-encode
base64-decode
base64-encode
bitcoin160
bitcoin256
btc-to-satoshi
ec-add
ec-add-secrets
ec-multiply
ec-multiply-secrets
ec-new
ec-to-address
ec-to-public
ec-to-wif
fetch-balance
fetch-header
fetch-height
357
fetch-history
fetch-stealth
fetch-tx
fetch-tx-index
hd-new
hd-private
hd-public
hd-to-address
hd-to-ec
hd-to-public
hd-to-wif
help
input-set
input-sign
input-validate
message-sign
message-validate
mnemonic-decode
mnemonic-encode
ripemd160
satoshi-to-btc
script-decode
script-encode
script-to-address
seed
send-tx
send-tx-node
send-tx-p2p
settings
sha160
sha256
sha512
stealth-decode
stealth-encode
stealth-public
stealth-secret
stealth-shared
tx-decode
tx-encode
uri-decode
uri-encode
validate-tx
watch-address
wif-to-ec
wif-to-public
wrap-decode
wrap-encode
For more information, see the Bitcoin Explorer homepage and Bitcoin
Explorer user
documentation.
358
|
Appendix G: Bitcoin Explorer (bx) Commands
Examples of bx Command Use
Let’s look at some examples of using Bitcoin Explorer commands to
experiment with
keys and addresses.
Generate a random “seed” value using the seed command, which uses the
operating
system’s random number generator. Pass the seed to the ec-new command to
generate
a new private key. We save the standard output into the file private_key:
$ bx seed | bx ec-new > private_key
$ cat private_key
73096ed11ab9f1db6135857958ece7d73ea7c30862145bcc4bbc7649075de474
Now, generate the public key from that private key using the ec-to-public
com‐
mand. We pass the private_key file into the standard input and save the
standard out‐
put of the command into a new file public_key:
$ bx ec-to-public < private_key > public_key
$ cat public_key
02fca46a6006a62dfdd2dbb2149359d0d97a04f430f12a7626dd409256c12be500
We can reformat the public_key as an address using the ec-to-address
command.
We pass the public_key into standard input:
$ bx ec-to-address < public_key
17re1S4Q8ZHyCP8Kw7xQad1Lr6XUzWUnkG
Keys generated in this manner produce a type-0 nondeterministic wallet.
That means
that each key is generated from an independent seed. Bitcoin Explorer
commands
can also generate keys deterministically, in accordance with BIP-32. In
this case, a
“master” key is created from a seed and then extended deterministically to
produce a
tree of subkeys, resulting in a type-2 deterministic wallet.
First, we use the seed and hd-new commands to generate a master key that
will be
used as the basis to derive a hierarchy of keys:
$ bx seed > seed
$ cat seed
eb68ee9f3df6bd4441a9feadec179ff1
$ bx hd-new < seed > master
$ cat master
xprv9s21ZrQH143K2BEhMYpNQoUvAgiEjArAVaZaCTgsaGe6LsAnwu-
beiTcDzd23mAoyizm9cApe51gNfLMkBqkYoWWMCRwzfuJk8RwF1SVEpAQ
We now use the hd-private command to generate a hardened “account” key and
a
sequence of two private keys within the account:
$ bx hd-private --hard < master > account
$ cat account
xprv9vkDLt81dTKjwHB8fsVB5QK8cGnzveChzSrtCfvu3aMWvQaThp59ueu-
fuyQ8Qi3qpjk4aKsbmbfxwcgS8PYbgoR2NWHeLyvg4DhoEE68A1n
Bitcoin Explorer (bx) Commands
|
359
$ bx hd-private --index 0 < account
xprv9xHfb6w1vX9xgZyPNXVgAhPxSsEkeRcPHEUV5iJcVEsuUEACvR3NRY3fpGhcnBiDbvG4LgndirD-
sia1e9F3DWPkX7Tp1V1u97HKG1FJwUpU
$ bx hd-private --index 1 < account
xprv9xHfb6w1vX9xjc8XbN4GN86jzNAZ6xHEqYxzbLB4fzHFd6VqCLPGRZFsdjsuMVERadbgDb-
ziCRJru9n6tzEWrASVpEdrZrFidt1RDfn4yA3
Next, we use the hd-public command to generate the corresponding sequence
of two
public keys:
$ bx hd-public --index 0 < account
xpub6BH1zcTuk-
tiFu43rUZ2gXqLgzu5F3tLEeTQ5t6iE3aQtM2VMTxMcyLN9fYHiGhGpQe9QQYmqL2eYPFJ3vezHz5wza
SW4FiGrseNDR4LKqTy
$ bx hd-public --index 1 < account
xpub6BH1zcTuktiFx6CzhPbGjG3UYQ13WR16CmtbPiagEKpEVtpyjshWy-
MaMV1cn7nUPUkgQHPVXJVqsrA8xWbGQDhohEcDFTEYMvYzwRD7Juf8
The public keys can also be derived from their corresponding private keys
using the
hd-to-public Команда:
$ bx hd-private --index 0 < account | bx hd-to-public
xpub6BH1zcTuk-
tiFu43rUZ2gXqLgzu5F3tLEeTQ5t6iE3aQtM2VMTxMcyLN9fYHiGhGpQe9QQYmqL2eYPFJ3vezHz5wza
SW4FiGrseNDR4LKqTy
$ bx hd-private --index 1 < account | bx hd-to-public
xpub6BH1zcTuktiFx6CzhPbGjG3UYQ13WR16CmtbPiagEKpEVtpyjshWy-
MaMV1cn7nUPUkgQHPVXJVqsrA8xWbGQDhohEcDFTEYMvYzwRD7Juf8
We can generate a practically limitless number of keys in a deterministic
chain, all
derived from a single seed. This technique is used in many wallet
applications to gen‐
erate keys that can be backed up and restored with a single seed value.
This is easier
than having to back up the wallet with all its randomly generated keys
every time a
new key is created.
The seed can be encoded using the mnemonic-encode Команда:
$ bx hd-mnemonic < seed > words
adore repeat vision worst especially veil inch woman cast recall dwell
appreci-
ate
The seed can then be decoded using the mnemonic-decode Команда:
$ bx mnemonic-decode < words
eb68ee9f3df6bd4441a9feadec179ff1
Mnemonic encoding can make the seed easier to record and even remember.
360
|
Appendix G: Bitcoin Explorer (bx) Commands
Index
Symbols
$ symbol, 33
A
accounts receivable (AR), 151
acknowledgments, xviii-xxii
addresses (see also keys and addresses)
algorithms used to create, 65
Base58 and Base58check encoding, 66-70
bitcoin wallet quick start example, 9
change addresses, 20
multisig addresses, 81, 274
security of, 10
vanity addresses, 82-88
application-specific integrated circuits (ASIC),
27
asymmetric cryptography, 57
ATMs, locating, 11
attribution, xvi
authentication, 191
authentication paths, 203
autogen/configure/make system, 35
(see also Bitcoin Core)
B
balanced trees, 203
balances, 119
Base58 and Base58check encoding, 66-70
Basics of Lightning Technology (BOLT), 297
binary hash trees (see merkle trees)
bitcoin
benefits of, xiii-xiv, 11
defined, 1-2
getting started, 6-14
history of, 4
overview of, 15-30
use cases, 5-6
Bitcoin Block Explorer, 16
Bitcoin Core
alternatives to, 51-53
architecture, 32
Bitcoin Core API, 43-51
exploring and decoding transactions, 45
exploring blocks, 47
RPC commands, 43
status information, 44
using programmatic interface, 48
compiling from source code, 32-37
build configuration, 34
core executables, 37
downloading, 32
version selection, 33
reference implementation, 31
running core nodes, 38-43
configuring, 39
database options, 41
first run, 39
Bitcoin Explorer (bx) commands, 357-360
bitcoin improvement proposals
Address Format for P2SH (BIP-13), 153
Block v2, Height in Coinbase (BIP-34), 263
CHECKHASHVERIFY (BIP-17), 225
CHECKLOCKTIMEVERIFY (BIP-65), 158,
264
CHECKSEQUENCEVERIFY (BIP-112),
160
Encrypted Private Keys (BIP-38), 80, 89
361
Hierarchical Deterministic Wallets (BIP-32/
BIP-44), 31, 96
Mnemonic Code Words (BIP-39), 31, 97,
99-105
Multipurpose HD Wallet Structure
(BIP-43), 97
Pay to Script Hash (BIP-16), 81, 225
Peer Authentication (BIP-150), 191
Peer-to-Peer Communication Encryption
(BIP-151), 191
Relative lock-time using consensus-
enforced sequence numbers (BIP-68),
160
repository of, 324
snapshot of, 324-327
Strict DER signatures (BIP-66), 264
types of, 323
Version bits with timeout and delay (BIP-9),
264
bitcoin network
Bitcoin Relay Networks, 176
bloom filters, 185-190
defined, 171
encrypted connections, 191
extended network activities, 173
extended network discovery, 176-180
full nodes, 180
node types and roles, 172-173
peer-to-peer architecture, 171
SPV nodes, 183-185
syncing the blockchain, 181
transaction pools, 192
bitcoin nodes
defined, 25
full nodes, 181, 189
mining nodes, 173, 219
network discovery, 176-180
running core nodes, 38-43
SPV nodes, 183-192, 207
types and roles, 172-173
bitcoin whitepaper, 31, 305-316
BitcoinAverage, 12
bitcoinfees (third-party service), 128
Bitcore, 343-345
Bitmask Sighash Modes, 143
BitPay Insight, 16
bloat, 155
blockchain (the)
block headers, 197, 227
362
| Index
block identifiers, 197
block structure, 196
blockchain forks, 240-247
full blockchain nodes, 180
genesis block, 28, 180, 198, 225
linking blocks in the blockchain, 200
merkle trees, 201-207, 227
nonpayment data recording, 155
overview of, 195
overview of mining, 26-29
syncing the blockchain, 181
test blockchains, 207-211
blockchain applications
benefits of bitcoin system, 275
building blocks for (primitives), 276
colored coins, 278-283
Counterparty, 283
examples of, 278
payment (state) channels, 284-297
routed payment channels, 297-304
(see also Lightning Network)
warnings and cautions, xvi
blockchain bloat, 155
blockchain explorer sites, 15
blockchain.info, 16
BlockCypher Explorer, 16
blocks
aggregating transactions into, 220-226
assembling and selecting chains of, 239-247
block hash, 47, 195, 197
block height, 47, 195, 197
candidate blocks, 28, 220
exploring with Bitcoin Core API, 47
genesis block, 28, 180, 195, 198, 225
headers, 197, 227
linking blocks in the blockchain, 200
mining transactions in, 27
new block validation, 238
parent blocks, 195, 227
structure of, 196
bloom filters, 185-190
brainwallets, 100
build documentation, 34
(see also Bitcoin Core)
Byzantine Generals' Problem, 4
C
candidate blocks, 28, 220
central trusted authority, 4, 15, 213
chain of transactions, 19
change addresses, 20
change, making, 20, 120
charitable donations, 5, 130, 143
Check Lock Time Verify (CLTV), 158-160
CHECKHASHVERIFY (CHV), 225
CHECKMULTISIG bug workaround, 150
CHECKSEQUENCEVERIFY (CSV), 162
child key derivation (CKD), 106
clearing, 14
(see also confirmations)
clients, libraries, and toolkits, 51-53
cloning source code, 33
code examples, obtaining and using, xv-xvi, 32
Coin ATM Radar, 11
coinbase transactions, 120, 196, 221-226
coinbase data, 225
rewards and fees, 223
structure of, 224
cold storage, 7, 110, 273
(see also storage)
collisions, 228
colored coins, 278-283
comments and questions, xvii
commitment, 141
Compact Block optimization, 176
conditional clauses, 164-167
configuration options, 40
(see also Bitcoin Core)
confirmations (see also mining and consensus;
transactions)
bitcoin wallet quick start example, 14
of large-value transactions, 255
role in transactions, 28
of small-value transactions, 26
consensus (see mining and consensus)
contact information, xvii
core executables, 37
(see also Bitcoin Core)
Counterparty, 283
cryptographic puzzles, 132
cryptography (see also keys and addresses)
asymmetric, 57
defined, 55
elliptic curve cryptography, 57, 60-63
currency creation, 215
currency exchanges, 11
D
data recording (nonpayment data), 155
decentralized systems
benefits of, xiv
bitcoin as, xiii, 270
bitcoin mining and, 213
bitcoin overview, 15-30
vs. centralized, 3
consensus in, 4, 217
in nature, xiv
security of, 269
deflationary money, 216
denial-of-service attacks, 131, 254 (see also
security)
deserialization, 122
deterministic initialization, 145
deterministic wallets, 94
(see also wallets)
development environment
consensus software development, 266
setup (see Bitcoin Core)
test blockchains and, 211
digital asset executors, 274
digital asset management, 278
digital currencies
benefits of bitcoin, 11
bitcoin vs. others, xiii
cryptocurrency, 56
currency exchanges, 11
prior to bitcoin, 3
digital keys (see keys and addresses)
digital notary services, 155, 278
digital ownership, 284
digital signatures
algorithm used, 138
asymmetric cryptography and, 57
defined, 139
how they work, 139
purpose of, 55
purposes of, 139
randomness in, 145
signature hash types, 141
verifying, 141
Distinguished Encoding Rules (DER), 140
distributed computing, 4
distributed version control systems, 33
DOCPROOF prefix, 156
documentation, 34
double-spend problem, 4
Index
|
363
dumpprivkey command, 59
dynamic fees, 127
E
Electrum wallet, 100
(see also wallets)
elliptic curve cryptography, 57, 60-63
Elliptic Curve Digital Signature Algorithm
(ECDSA), 138, 143
emergent consensus, 217
encryption, 55, 191 (see also keys and
addresses)
Enhanced Padded-Order-Based Coloring
(EPOBC), 279
entropy
os.urandom (see random numbers)
random number generation, 59, 79, 145
EQUAL opcode, 166
EQUALVERIFY opcode, 166
Ethereum Virtual Machine (EVM), 283
exchange rates
determining, 11, 16
floating, 12
listing services, 11
extended keys, 108
extrinsic asset management, 278, 283
F
Falcon Relay Network, 176
Fast Internet Bitcoin Relay Engine (FIBRE), 176
fees
dynamic fees, 127
fee relay policies, 127
fee sniping, 163
mining rewards, 214
static fees, 128
transaction fees, 18, 126, 213, 223
floating exchange rate, 12
flooding technique, 25
flow control, 164-167
forks
blockchain fork events, 240-247
changing consensus rules, 256-266
contentious hard forks, 260
diverging miners and difficulty, 259
hard forks, 256
soft fork activation, 262
soft fork drawbacks, 262
soft forks, 261
364
| Index
software forks, 258
fractional values, 18
full indexing option, 41
full-node clients, 7, 172, 180
G
generator point, 60, 63
genesis block, 28, 180, 195, 225
getting started
acquiring bitcoin, 10
confirmations, 14
exchange rates, 11
quick start example, 8-10
sending and receiving bitcoin, 12
wallet selection, 6-8
warnings and cautions, xvi
GitHub bitcoin page, 32
guard clauses, 165
H
halvings, 223
hard forks, 260, 267
hardened derivation, 112
hardware wallets, 97, 110, 273 (see also wallets)
Hash Time Lock Contracts (HTLC), 296
headers, 197, 227
hierarchical deterministic (HD) wallets, 94, 96,
106, 113
(see also wallets)
I
IF clauses, 165
inputs (see outputs and inputs)
intended audience, xiii
issuance rate, 215
J
JBOK wallets, 94
(see also wallets)
K
key derivation methods, 94
key utility (ku), 347
key-stretching function, 101
keychains, 93
keys and addresses (see also public and private
keys)
advanced forms, 80-91
encrypted private keys, 80
paper wallets, 88
pay-to-script hash and multisig
addresses, 81
vanity addresses, 82
bitcoin addresses, 64-76
Base58 and Base58check encoding, 66
key formats, 70
implementing in Python, 76-79
overview of, 55-64
elliptic curve cryptography, 60
key pairs, 57
private and public key pairs, 57
private key generation, 58
public key calculation, 60
public key cryptography, 56
public key generation, 63
warnings and cautions, xvi
L
libraries, clients, and toolkits, 51-53
Lightning Network
basic example, 298
benefits of, 303
defined, 297
transport and routing, 301
lightweight clients, 8, 172
locking scripts, 121, 132
M
mainnet, 207
(see also blockchain (the))
malleability, 46
Median-Tme-Past, 162
memory pools (mempools), 192, 220
merkle trees, 201-207, 227
milli-bitcoin, 18
millibits, 17
mining and consensus
aggregating transactions into blocks,
220-226
assembling and selecting chains of blocks,
239-247
blockchain forks, 240
bitcoin economics and currency creation,
215
coinbase transactions, 120
consensus attacks, 253-256
consensus rules
changing, 256-262
satisfying, 2
security provided by, 26
consensus software development, 266
constructing block headers, 227
decentralized consensus, 213, 217
defined, 228
emergent consensus, 217
hashing power race, 247-253
independent transaction verification, 218
mining farms and pools, 27
mining nodes, 173, 219
mining rewards and fees, 214
mining the block, 228-238
retargeting to adjust difficulty, 235
successful completion, 237
target representation, 235
new block validation, 238
overview of, 26-29
Proof-of-Work algorithm, 4, 27, 173, 214,
220, 228-234
purpose of, 213
rewards and fees, 126, 223
security and consensus, 271
mining pools, 250-253
benefits of, 250
defined, 27
managed pools, 252
operation of, 28, 251
peer-to-peer pools (P2Pool), 252
minrelaytxfee option, 127
mnemonic code words, 94, 97, 99-105
money supply, 215
multisig addresses, 81, 274
multisignature scripts, 149, 167
N
Nakamoto, Satoshi, 4, 31, 305-316
nLocktime field, 157
nodes (see bitcoin nodes)
nonce values, 225, 249
nondeterministic wallets, 94
(see also wallets)
nonpayment data, 155
nSequence field, 160
O
off-blockchain transactions, 270
offshore contract services, 5
Index
|
365
opcodes
EQUAL, 166
EQUALVERIFY, 166
redefinition by soft forks, 261
VERIFY, 165
Open Assets, 279
open source licenses, xvi, 4, 31, 316
OpenSSL cryptographic library, 64
orphan pools, 192
outputs and inputs
basics of, 18
creating outputs, 24
defined, 21 наput components, 123
input serialization, 125
locating and tracking inputs, 22
output characteristics, 119
output parts, 121
outputs defined, 119
structure of, 122
P
paper wallets, 88-91, 273 (see also wallets)
parent blocks, 195, 227
parsing, 122
passphrases, 102, 104
passwords
core node first run, 39
creating, 39
encrypted private keys, 80
survivability and, 274
Pay-to-Public-Key-Hash (P2PKH), 131, 136
Pay-to-Script-Hash (P2SH)
addresses, 153
benefits of, 154
coinbase data, 225
import/export example, 151
multisig addresses and, 81
redeem scripts and validation, 154
payment (state) channels
asymmetric revocable commitments,
292-296
building blocks (primitives) used in, 278
concept of, 284
defined, 284
example of, 286-288
Hash Time Lock Contracts (HTLC), 296
making trustless channels, 289-292
terminology, 285
366
|
Index
payment requests, 17
PBKDF2 function, 101
peer-to-peer (P2P), 171
Peer-to-Peer authentication and encryption,
191
peer-to-peer pools (P2Pool), 252
pool operators, 252
(see also mining pools)
primitives, 276
privacy, maintaining, 11, 185-192
programmable money, 131
programmatic interface, 48-51
Proof of Existence, 156, 278
Proof-of-Work algorithm, 4, 27, 173, 214, 220,
228-234
propagation
address propagation and discovery, 178
flooding technique, 25
process of, 25
relay networks and, 176
public and private keys (see also keys and
addresses)
child key derivation (CKD), 106
compressed private keys, 75
compressed public keys, 73
encrypted private keys, 80
extended keys, 108
hardened child key derivation, 112
key pairs, 56
ephemeral, 144
private key formats, 70
public child key derivation, 109
public key formats, 72
pybitcointools, 76
pycoin library, 347
Q
QR codes
bitcoin wallet quick start example, 9
payment requests, 17
warnings and cautions, xvi, 17
R
random numbers
os.urandom (see entropy)
random number generation, 59, 79, 145
redeem scripts, 152, 154
reference implementation (see Bitcoin Core)
regtest (Regression Testing), 210
relative timelocks, 160-162
relay networks, 176
resource requirements, 38
RETURN operator, 155
risk, balancing and diversifying, 273
(see also security)
root of trust concept, 271
root seeds, 106
routed payment channels (see Lightning Net‐
work)
S
salts, 102
satoshi, xxx
Satoshi client, 31, 181
satoshis, 18, 119
scripting
complex script example, 167-169
data recording output, 155
flow control scripts, 164-167
locking scripts, 121, 132
multisignature scripts, 149-151
CHECKMULTISIG bug, 150
import/export example, 167
Pay-to-Script-Hash, 151-155
addresses, 153
benefits of, 154
import/export example, 151
redeem scripts and validation, 154
redeem scripts, 152
Script language operators, constants, and
symbols, 317-321
timelocks, 157-164
Check Lock Time Verify (CLTV), 158
defense against fee-sniping, 163
Median-Tme-Past, 162
nLocktime, 157
relative timelocks, 160
relative timelocks with CHECKSE‐
QUENCEVERIFY, 162
relative timelocks with nSequence, 160
uses for, 157
transactions and, 131-137
scriptPubKey, 121, 132
scriptSig, 132
security (see also warnings and cautions)
bitcoin addresses, 10
consensus attacks, 253-256
defense against fee-sniping, 163
denial-of-service attacks, 131, 254
locking and unlocking scripts, 136
maintaining privacy, 11, 185-192
passwords, 39, 80, 274
security principles, 269-272
user security best practices, 272-274
vanity addresses, 87
wallet selection, 6
segnet, 210
segwit (Segregated Witness), 210, 329-342
serialization
inputs, 125
outputs, 122
shell commands, 33
SIGHASH flags, 141
simple-payment-verification (SPV), 8, 29, 172,
183-185, 207
smart contracts, 283
sniping, 163
soft forks
activation, 262
defined, 261
drawbacks of, 262
redefinition of NOP codes, 261
source code, cloning, 33
(see also Bitcoin Core)
spending bitcoin (see also transactions)
bitcoin wallet quick start example, 12
defined, 19
double-spend problem, 4
simple-payment-verification (SPV), 29
stateless verification, 132
static fees, 128
storage
cold storage, 7, 110, 273
physical bitcoin storage, 273
survivability, 274
syncing, 181
T
targets, 231, 235-237
terminal applications, 33
testnet, 207-209
The Onion Routing network (Tor), 191
third-party API clients, 8, 51-53
timelocks
Check Lock Time Verify (CLTV), 158
defense against fee-sniping, 163
Median-Tme-Past, 162
Index
|
367
nLocktime, 157
relative timelocks, 160-162
uses for, 157
toolkits, libraries, and clients, 51-53
Tor network, 191
transaction IDs (txd), 46, 124
transaction IDs (txid), 189, 282, 338
transaction pools, 192, 220
transaction utility (TX), 353-355
transactions
advanced, 149-169
data recording output, 155
example, 167
flow control scripts, 164
multisignature scripts, 149, 167
Pay-to-Script-Hash, 151
timelocks, 157
aggregating into blocks, 220-226
behind the scenes details of, 118
coinbase transactions, 120, 196, 221-226
constructing, 22-26
database configuration options, 41
defined, 18, 21, 117
digital signatures and, 138-145
exploring with Bitcoin Core API, 45
higher-level abstractions, 145-148
independent verification of, 218
off blockchain, 270
orphaned, 192
outputs and inputs, 119-130
input components, 123
input serialization, 125
output characteristics, 119
output components, 121
structure of, 122
transaction fees, 126
overview of, 18-22
parsing, 122
scripts and Script language, 131-137,
317-321
valid and invalid, 134
warnings and cautions, xvi, 17
Turing incompleteness, 131
txindex option, 41
typographical conventions, xiv
U
unlocking scripts, 132
368
|
Index
unspent transaction outputs (UTXO), 119, 123,
155
use cases
buying coffee, 8-14, 16-30, 45-50, 117-126,
130, 136, 140-148, 157-160, 166, 220,
254, 332-337
charitable donations, 5, 130, 143
import/export, 6, 151-153, 167-169,
333-334, 337
mining for bitcoin, 6, 27, 219-228, 237-238
offshore contract services, 5, 30, 82
retail sales, 5, 254-255
user security best practices, 272-274
web store, 5, 98-99, 110-112
UTXO sets, 119, 123, 155
V
validation, 154, 238
vanity addresses, 82-88
VERIFY opcodes, 165
virtual asset management, 283
W
wallets
best practices for, 31, 97
constructing transactions, 22
contents of, 93
defined, 93
quick start example, 8-10
selecting, 6-8
technology of
creating HD wallets from root seed, 106
mnemonic code words, 99
seeds and mnemonic codes, 97
using extended public keys on web
stores, 110
types of
deterministic (seeded) wallets, 95
hardware wallets, 98, 273
hierarchical deterministic (HD) wallets,
96
JBOK wallets, 94
nondeterministic (random) wallets, 94
paper wallets, 88-91, 273
primary distinctions, 94
using bitcoin wallets, 98
warnings and cautions (see also security)
accidental bitcoin locking, 155
avoid sending money to addresses appear‐
ing in book, xvi, 17
change outputs, 130
core node resource requirements, 38
digital signatures, 145
password creation, 39
private key protection, 58
whitepaper, 305-316
witnesses, 55, 121, 132
Index
|
369
About the Author
Andreas M. Antonopoulos is a noted technologist and serial entrepreneur
who has
become one of the most well-known and well-respected figures in bitcoin.
As an
engaging public speaker, teacher, and writer, Andreas makes complex
subjects acces‐
sible and easy to understand. As an advisor, he helps startups recognize,
evaluate, and
navigate security and business risks.
Andreas grew up with the internet, starting his first company, an early
BBS and
proto-ISP, as a teenager in his home in Greece. He earned degrees in
computer sci‐
ence, data communications, and distributed systems from University College
London
(UCL)—recently ranked among the world’s top 10 universities. After moving
to the
United States, Andreas cofounded and managed a successful technology
research
company, and in that role advised dozens of Fortune 500 company executives
on net‐
working, security, data centers, and cloud computing. More than 200 of his
articles on
security, cloud computing, and data centers have been published in print
and syndi‐
cated worldwide. He holds two patents in networking and security.
In 1990, Andreas started teaching various IT topics in private,
professional, and aca‐
demic environments. He honed his speaking skills in front of audiences
ranging in
size from five executives in a boardroom to thousands of people in large
conferences.
With more than 400 speaking engagements under his belt he is considered a
world-
class and charismatic public speaker and teacher. In 2014, he was
appointed as a
teaching fellow with the University of Nicosia, the first university in
the world to offer
a masters degree in digital currency. In this role, he helped develop the
curriculum
and cotaught the Introduction to Digital Currencies course, offered as a
massive open
online course (MOOC) through the university.
As a bitcoin entrepreneur, Andreas has founded a number of bitcoin
businesses and
launched several community open source projects. He serves as an advisor
to several
bitcoin and cryptocurrency companies. He is a widely published author of
articles
and blog posts on bitcoin, a permanent host on the popular Let’s Talk
Bitcoin pod‐
cast, and a frequent speaker at technology and security conferences
worldwide.
Colophon
The animal on the cover of Mastering Bitcoin is a leafcutter ant (Atta
colombica). The
leafcutter ant (a nongeneric name) is a tropical, fungus-growing ant
endemic to
South and Central America, Mexico, and southern United States. Aside from
humans, leafcutter ants form the largest and most complex animal societies
on the
planet. They are named for the way they chew leaves, which serve as
nutrition for
their fungal garden.
Winged ants, both male and female, take part in a mass exit of their nest
known as
the revoada, or a nuptial flight. Females mate with multiple males to
collect the 300
million sperm necessary to set up a colony. Females also store bits of the
parental fun‐
gus garden mycelium in the infrabuccal pocket located in their oral
cavity; they will
use this to start their own fungal gardens. Once grounded, the female
loses its wings
and sets up an underground lair for her colony. The success rate for new
queens is
low: 2.5% establish a long-lived colony.
Once a colony has matured, ants are divided into castes based on size,
with each caste
performing various functions. There are usually four castes: minims, the
smallest
workers that tend to the young and fungus gardens; minors, slightly larger
than min‐
ima, are the first line of defense for the colony and patrol the
surrounding terrain and
attack enemies; mediae, the general foragers that cut leaves and bring
back leaf frag‐
ments to the nest; and majors, the largest worker ants that act as
soldiers, defending
the nest from intruders. Recent research has shown that majors also clear
main forag‐
ing trails and carry bulky items back to the nest.
Many of the animals on O’Reilly covers are endangered; all of them are
important to
the world. To learn more about how you can help, go to
animals.oreilly.com.
The cover image is from Insects Abroad. The cover fonts are URW Typewriter
and
Guardian Sans. The text font is Adobe Minion Pro; the heading font is
Adobe Myriad
Condensed; and the code font is Dalton Maag’s Ubuntu Mono.